
我々の住むこの宇宙はどの様に構成され、そしてどのように始まったか?これは遠い昔から人類が抱いてきた最大の疑問の一つと言えよう。物理学の一分野である宇宙論は、その様な疑問に答えようとする学問だ。現代の宇宙論では、ごく小さな点からビッグバンにより爆発的に広がり現在の大宇宙が構成された言う、なんとも壮大なシナリオを提示してくれている。しかし本当に宇宙論を理解しようとすると相対性理論と量子論を理解しなければならない。だが、これらの学問は大学の物理学科でもなければ学ぶ機会はないだろう。本ノートは相対性理論の数式が何を意味しているかを整理し、相対性理論で何が記述できるかを”実感”することを目的とし書き下した。
相対性理論は特殊相対性理論と一般相対性理論との二段構成になっているが本編では特殊相対性理論におけるローレンツ変換までをカバーする。続編および後続の一般相対性理論のノートと併せて、最終目標はブラックホールのシュバルツシルト解を導出するまでとする。尚、数式より図解の比重が多く、超入門的な内容となる。
加えて、本編に出てくる数式を自ら応用できる程度に理解を深められるよう、Mathematica・Maximaによる数式処理や、グラフィック化の方法の解説部(CAS-Lab/計算機代数コーナー)と連携させる予定だ。
1.1 光速度不変の原理

光や電波の真空中の速度は約30万km/秒だ。光と電波は同じものであり、それぞれ電磁波の一形態といえる。歴史的にいうとマックスウェルは、ファラデーによって発見された電磁気に関する諸法則を、数学的に整理し、電磁気学を完成させた。そしてその中で電磁波の存在と、その速度を30万km/秒と予測した。その後電磁波の理論予測30万km/秒と光の実測時の一致が確認され、光は電磁波の一種であり、単に周波数の高いものが光、低いものが電波と理解されるようになった。
ところでこれに対し、早い光とか遅い光とかは在るのだろうか? 『xx天問台、世界最高速の光を発見。なんと、33万km/秒。3年ぶりに記録を更新!』 想像すると面白ことだが、このようなニュースはついぞ聞かない。秒速50mで走っている自動車のヘッドライトから出る光は、止まっている自動車のヘッドライトから出る光より50m/秒だけ早くてもいいような気がする。はたして、実際はどうなっているのだろうか。
水面上の波は発した物体の速度に関係無く一定の速度で広がって行く。やはり光はこのようにな伝わり方をするのだろうか。
『星からの光も宇宙の海を波の様に伝わって来るのだろう。きっと光を伝える水のような媒体が宇宙を満たしているのだ』 19世紀の物理学者たちはこの媒体をエーテルと呼び『地球は宇宙に満ちたエーテルの海の中を走り回っているのだ。さすれば地球上ではエーテルの風が吹いていることになる。だとしたら測る向きによって光の速度が異なってくるはずだ』と考えた。
しかし結果はエーテルの風など吹いていなかった。マイケルソン、モリーによる実験が有名で、精巧な光の干渉計を用いて、90度異なる向きの光の速度差を測れるものだった。しかし何度も場所を変え、季節を変えて実験は繰り返えされたが結果はいつも同じ『速度差は無い』であった。光の速度はいつでも、どこでも、だれにでも30万km/秒であったのだ。
1.2 相対性原理
相対性原理は相対性理論の教科書の中に『全ての物理法則は、いかなる慣性系を基準にとっても、全く同じ形式で表現される』と書かれているのだが、どうも実感がわかない。具体的にどのような事なのか?
それでは、ここで思考実験を行ってみよう。あなたも是非、お付き合いいただきたい。
まずは、時間を計測するために、測定装置である時計を集めよう。最初は最も一般的なもの。クオーツ式の腕時計。
![]() あなたも、色々な方式や原理の異なる時計を考えてみてほしい。例えば、蚊取り線香時計などでもよい。
あなたも、色々な方式や原理の異なる時計を考えてみてほしい。例えば、蚊取り線香時計などでもよい。
この時計の原理は、線香が燃えて短くなっていく長さで時間が計れる。立派な時間測定装置だ。尚、精度は問題としない。この思考実験室内では、全ては理想的な状態となる。常に完璧な精度が得られると考えてよい。だからどんな安物の時計でも高級時計でも同様に完璧な精度となると考えてほしい。
ということで、その例として、もう一つ、ちょっと変わった時計を。モヤシ時計だ。
 これは水を与えると根がどんどん伸びてゆく。その伸びる長さで時間を計れる。このモヤシは1時間で1mm伸びる。動作原理は、生化学反応とでも言っておこう。ご存知のとおり、この植物のマメの部分に蓄えられた栄養分を使って根の細胞を分裂させて伸びて行く。
これは水を与えると根がどんどん伸びてゆく。その伸びる長さで時間を計れる。このモヤシは1時間で1mm伸びる。動作原理は、生化学反応とでも言っておこう。ご存知のとおり、この植物のマメの部分に蓄えられた栄養分を使って根の細胞を分裂させて伸びて行く。

脈拍時計? なるほど、これは面白い!
最後の実験時計として、アインシュタイン博士が考案した光時計を紹介しよう。

この時計は、二枚の合わせ鏡の間を光、今回はレーザーパルスが反射しながら往復する。その往復の回数を数えることにより、時間が測定できるというものだ。ざっと言うと、光の速度を、勿論、レーザー光線も通常の光と同様だから、30万Km/秒として、1.5mの鏡の間を往復させると通過距離は3mとなる。よって1往復に1億分の1秒かかるということになる。
ちなみに千分の1秒は1ミリ秒(1mS)、百万分の1秒は1マイクロ秒(1μS)、10億分の1秒は1ナノ秒(1nS)と呼ぶ、従って、この場合の往復時間は10ナノ秒ということだ。
まあ、これも実用化できるかどうかはさておき、他の時計と同様に実験室の中では理想状態であるから、長時間でも問題無く使用できる。いや、むしろ他の変な時計と比べずっと安心できると思えるのだが。
それではそろそろ実験室を宇宙船に搭載して、宇宙空間の実験場に移動しょう。
宇宙船はS号、S’号の2隻用意してある。私はS号に、あなたはS’号に搭乗していただこう。もちろん実験用の時計は2組用意する。私の宇宙船S号はあなたより前方を航行している。あなたのS’号の方の速度が速いため、そのうち追い越されることになる。
そして実験内容はいたって単純。それぞれの宇宙船で、所定速度の慣性航行に移った後、一旦全ての時計を合わせ、その後どれかにずれが生じていないか確認するということだ。
どうだろう? あなたのいるS´号の時計はすべて一致しているだろうか?
さて、これは思考実験なので、あなたは自分の直観や考察を重ねた上で、『すべての時計は一致しているはずだ!』とも、『いや、速度の遅い早いが影響して、ずれてしまう時計があるはずだ!』とも答えることができる。
しかし相対性原理、つまり『全ての物理法則は、いかなる慣性系を基準にとっても、全く同じ形式で表現される』とは前者、『すべての時計は一致しているはずだ!』と主張していることと同じなのだ。
わたしは当然前者を支持しており、相対性原理の主張に納得している。そもそも、速度の違いで勝手に脈拍だけが遅くなったり、早くなったりするのは困るし、もし腹時計でも持ち込んだとして、速度次第でお腹が早くすいてしまうなどと、とんでもなく変な現象が起きかねなくなる。速度によって脈拍時計と腹時計がずれるという現象があり得るなら、心臓と胃腸が体の内部で不整合を起こしていることになる。それは私には少々困った事態である。
それでは、相対性原理に基づいてこの思考実験の続けてみよう。
ここで注目すべきは光時計だ。まずは私の手元の、S系で静止している光時計の解析をしよう。図1.2-1の様に鏡の間隔を l とし、光速度 c を3×08[m/S]をとする。下から上に到着するために要する時間 t0 は5n秒かかっている。
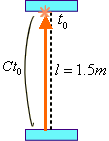
図1.2-1
次は、あなたから見たS系にある私の時計の解析。下記の図1.2-2の様に、光が到着するまでに鏡は当然移動する。
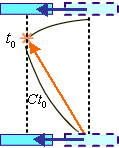
図1.2-2
しまり、t0 =5n 時間では到着できていない。到達できる時間を t1 とすると
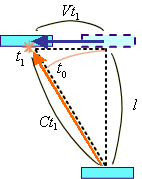
図1.2-3
逆に私のS系からあなたの光時計を観察する。向きは逆になるが、やはり同様に光が到達できる時間はt1 となっている。しかし、お互いに同じ光時計を見ているのだ。
それでは、他の時計はどうなっているのだろうか?残念ながらと言うべきか、うれしいことにと言うべきか、相対性原理に従い光時計と同じだけ遅れていなければならない。
以上の様に、相対的な速度差ですれ違う系の、すべての時計はお互いに遅れている。クオーツの時計は電子部品で作られて、電磁気理論や物性物理などが基盤となっている。蚊取り線香時計は燃焼反応で化学の分野だろう。モヤシ時計や脈拍時計、そしてもしあれば腹時計などは生化学分野に基づく。これらの時計が全て同じく遅れるということは、その系の時間そのものが遅れているということになる。
これは後ほど出てくるローレンツ変換で定式化されるが、自分のいる系、つまり静止している系の時間をtとし、すれ違う系、つまり自分に対して移動している方の系の時間をt’とすると
という関係式を得られる。以上が特殊相対性理論のつかみの部分となる。
1.3 同時性
静止系から見て、移動系との間では『同時』という概念が崩れてくる。 移動系内で同時に起きた事でも、静止系から見た場合、同時に起きたことにならなない。 もちろん逆に、こちらでの同時は、相手の移動系から見て、やはり同時では無くなるということになる。
尚、ここでは、我々のいる側の慣性系を静止系。相対的にすれ違って移動して行く慣性系を移動系と呼ぶことにする。
それでは、そのことを確認するする思考実験を行って見よう。尚、光の時間差を基に議論することになるが、その場合、『光が早く到着したとか、遅く到着したとか議論しても、それは単に見た目の問題で、物理、特に力学的に重要な意味を感じない!』と思われるかもしれない。そこで、光としては強力な金属切断用のレーザーを使って思考実験してみよう。
今度の実験装置は以下の図1.3-1のような構成だ。中央にレーザー発生装置がある。それぞれ前方向きと後方向きの二基が背中合わせで設置されている。
さらに前後両端には実験員が配置されている。 前方はAさん、後方はBさんだ。 中央から、前端、後端までそれぞれ300万Kmある。
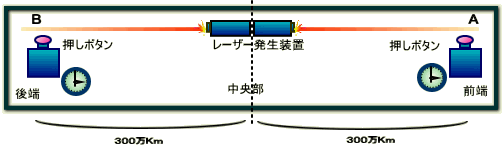
図1.3-1
レーザー光線は10秒周期でオフ・オンを繰り返す。下記の図3-2のように0.5秒間だけオフしその後9.5秒オンという周期だ。

図1.3-2
実験員のAさん、Bさんはボタンを定期的に押し続けなければならない。 何故かと言うと、実は15秒以上ボタンを押さないと、彼らの椅子に仕掛けてある爆弾が、爆発するようになっているからだ。ちょっと気の毒だが、真剣に実験に臨んでもらうためだ。ご協力いただこう。
さらに気の毒なことに、そのボタンを押すためには、先ほどのレーザー光線路を遮らなければならない。それの何が気の毒かと言うと、なんと、このレーザーは金属切断用だ。だから、光線が一瞬途切れる0.5秒の間に、すばやく押さなければなならない。
![]()
もたもたしていると、手が一瞬にして焼け切れる。光線がオフとなる期間はたったの0.5秒なので、途切れるのを確認してからボタンを押しに行っていたのでは、よほどの運動神経の持ち主でない限り間に合わないだろう。
そこで実験員達には時計を携帯することを許している。 ![]()

どんな時計でも結構だが、今回の実験員はクオーツ時計を選んだようだ。 そして時計で10秒のタイミングを計りながらボタンを押すことにする。
以降、説明では時計は秒針のみ注目する。つまり、時刻は0秒から59秒の間をぐるぐると回ってくりかえす。
さて、この実験装置を静止系ではなく、移動系の方に搭載して実験してもらおう。先ず最初は開始のタイミングを合わせるために、レーザー光線を時報よろしく、『ピ、ピ、ピー』と一秒間隔で光らせよう。この『ピー』の送出タイミングで、中央部の時計の秒針を0秒にセットし、移動系座標時間とする。AさんBさんは、受信タイミングで10秒にセットすればよい。そして、その時点から時限爆弾もセットされ、10秒間隔でレーザーをオン・オフが繰り返されるとしよう。
忘れないでいただきたい。レーザーの一瞬の途切れ(0.5Sのオフ)でボタンを押して、タイマーをリセットすることを繰り返さなければ、15秒後に爆発してしまう。このように実験員は延々と時計を握り締め、カウントダウンしながら10秒間隔でボタンを押し続けなければならない。
ウーン…ちょっとドキドキする。
ところで、この実験を行っている移動系内では、AさんもBさんも、もちろん同時にボタンを押していることになる。以下のこの実験の支配的原理により、二人の動作も0.5秒以内で正確に同期している事になる。
”オフの到来”=”10秒ごとの頭”
万が一、ずれてしまったら、どちらかの実験員の手がちょん切れてしまった(か、あるいはタイマーをリセットできずに爆発してしまったか?)という事になる。なんとも、気の毒な次第だ。
さて、しばらく見守っていたが、AさんもBさんも失敗することもなく順調にリセットを繰り返しているようなので、今度はこの実験状況を静止系の視点で考察してみよう。
静止系から見て最初に起きる事象は、静止系の中央部を移動系の中央部が通り過ぎることだ。
以下の図1.3-3の様に移動系実験装置の中央部が、静止系側の中央基準点を左から右に通り過ぎて行こうとしている。
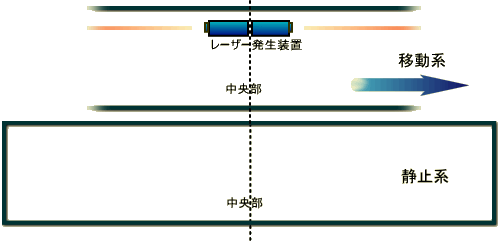
図1.3-3
実験前の準備として、中央部がすれ違う時点で静止系、移動系それぞれの秒針がピッタリと0となる様にタイミングを調整ている。9.5Sのオンが終わり0.5Sが始まる、ちょうど切り替わりのタイミングだ。
次に起きる事象は、Bさんにオフが到達するということだ。
その理由は簡単なことで、Bさんは静止系中央部に向かって近づいてきていから、その分早く到達することになる。

図3-4
しかし、その時実験室の後端にいるBさんの時計は、かならず10秒を指していなければならない。わざわざ、移動系と静止系の中央点がすれ違う時点で、双方の時間を合わせたのにもかかわらずである。なぜならBさんは図1.3-4の通りこの時計が10秒になるのを見ながら、オフの到来に合わせてボタンを押そうとしているとこだからだ。
”オフの到来” = ”10秒ごとの頭”
そう、我々は移動系にいたときに、この実験における支配的原理により、Bさんがこの時計を使って10秒ごとに到来する短いオフのタイミングを前もって知り、素早くボタンを押している様子を、さんざん観察してきたではないか。
ところで、この時点での、つまり静止系同時刻のAさんはどんな状況だろうか?
Aさんは遠ざかっている。したがって未だレーザのオフが届いていない。届いていない以上,Aさんの時計は10S未満でなければならない。
図1.3-5
もし、静止系にいるあなたがこの場所にたまたま居合わせたとして、Bさんがボタンを押しているタイミングだからといって、代わりにボタンを押すようなことは決してしない方がよい。目の前にあるレーザ光線は、決して錯覚でも気のせいでもない。現実の金属切断光線だからだ。


その後少ししてAさんの所に光線のオフが届く。同じくしてAさんの時計も10秒を指す。

同時にレーザもオフとなった。今だ!
この実験結果から、AさんBさんの時計の例で分かる様に『相対的に移動する慣性系では、その場所によって時刻が違っている』ということになる。つまり移動系の座標から静止系の座標に読み替える方法が必要になってくる。
1.4 時空
まず移動系でダイヤグラムを使ってこの実験を分析してみよう。下の図1.4-1aは、時間軸と、空間軸で表された座標の中に、物理的対象物(事象)がどの時刻に何処にいるのかをプロットしたものだ。列車がどの時間にどの位置にいるかを示す列車ダイヤと同じだ。
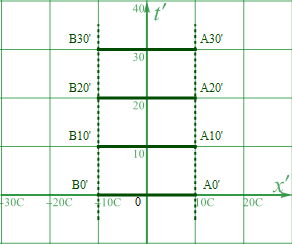
図1.4-1a
Aさん、Bさんの10秒毎にいる位置を示している。点線は軌跡を示しており、相対性理論では世界線と呼ばれる。実験装置は移動系S’上で静止しているため、A点、B点それ真上に伸びた世界線となる。ここで1光秒を大文字の”C”と省略することにしよう。1光秒は30万Kmだ。
図1.4-1bはさらにレーザー光の軌跡を加えてたものだ。
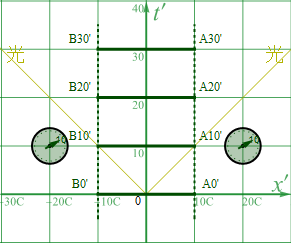
図4-1b
時刻0の瞬間に発せられたレーザー光の単発パルス(オンであれオフであれ)が 10C (300万Km) 離れたA、B両端に、10秒後に到達している様子が分かる。
尚、時空点(事象)を『A10’』の様にダッシュを付して書きこんでいる。これはS系での時刻と異なりS’における時刻を使っていることを示す。
今度は我々が観測していた側である静止系Sに立って、この実験装置をみてみよう。
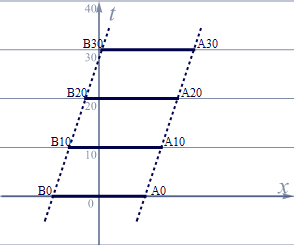
図1.4-2
図1.4-2の様に、実験装置は左から右移動して行く。移動速度が速ければ速いほど世界線は寝てくる。B0、A0 はS系での時刻 t=0 の時空点だ。これは丁度時刻0で実験装置の中央部が重なった瞬間のAさんBさんを表してる。
注目すべきは、静止系から見たA地点とB地点の、移動系における時刻が異なっていたことだ。前節の思考実験を思い出してもらいたい。
光のオフがBさんに届いた時点で、時刻は10秒を指していた。これは図4-3aのB10’に対応する。
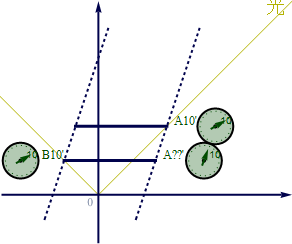
図1.4-3a
一方B10’の右端はA??’だが、まだ光のオフがとどいていない上、時計の針が10秒に満たない状態のAさんに対応する。静止系でのA??’に、たまたまあなたが居合わせたとして、ボタンに触れない方が良いと言った理由が分かると思う。B10’と同時刻なのにオフがまだ届いていない。
それでは、移動系での同時刻はいったい何処になるのだろうか? 丁度、光のオフが前端Aに到着した瞬間がそうだった。図ではA10’に相当する。
従って、同一時刻線を書き込むと下記図1.4-3b の様になる。このB10’とA10′ を結ぶ緑の線上の時計は、全て10秒を指していることになる。尚、この同一時刻線のx軸に対する傾きは、t軸に対する同一地点線(Bさんの世界線)と同じ角度で閉じている。
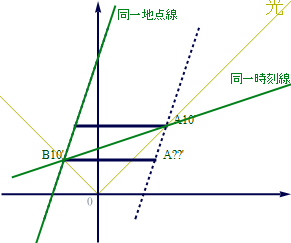
図1.4-3b
図1.4-4で大雑把に証明しよう。
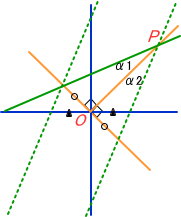
図4-4
原点Oを挟んで等距離の任意の平行線に対して、原点を通る全ての直線は、マル印の様に等距離になる。よって、光の軌跡45度線O,Pを挟むα1,α2の角度は等しくなる。
同一地点線の傾きは v/c であり、同一時刻線は c/v となる。
これらの事をたよりに、静止系Sの座標上に移動系S’の座標をメッシュ状に書きこんでみよう。
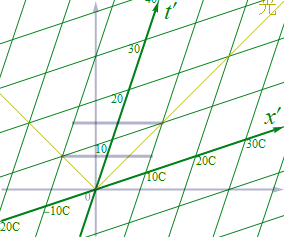
図1.4-5a
同一地点を繋げたものが時間座標に相当する。S’の時間軸は斜めに傾いている。
同様に、移動系S’での同一時刻を繋げたものが空間座標に相当する。これも斜めに傾いている。
さらに移動系内での同時刻(t’で10秒ごと)の実験装置の位置を重ねてみたのが図1.4-5bだ。
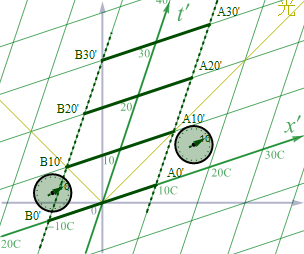
図1.4-5b
これは図1.4-1b を静止系から眺めた図となる。何と移動系の時空は斜交座標となっていた。
さて、これでS系から見た、S’系の時空絵図が出来あがった。しかし、まだS座標側に目盛りが振られていないので、指定の点のS座標が分からない。
それではS系の座標軸に目盛を振って完成させよう。
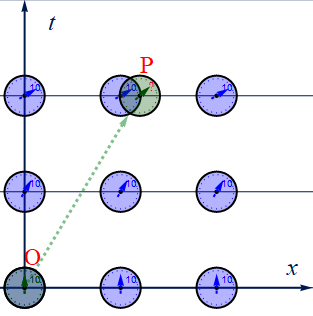
図1.4-6
原点Oで時刻[0秒]の移動系の時計が、P点に光速の0.6倍で移動していたとする。この場合、Pにおける移動系の時計の時刻[?]は、静止系の時計の時刻に対してEq1.2-1により、少ない時刻を指しているはずだ。
Pにおける時刻 t’ [?] の値は8秒
となる。また、移動系から静止系の時計を観測しても同様に8秒となっていた。
この関係は下記、図1.4-7での青い点線の矢印で示されるように、t軸1秒目盛りの静止系での同一時刻線とt’軸との交点の関係となる。
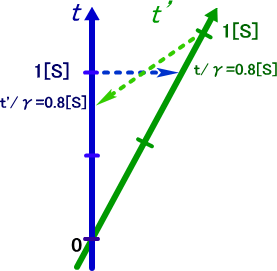
図1.4-7
一方、緑の点線の矢印は、図1.4-3b のように移動系における同一時刻を示しており、空間座標と同じ傾きだ。t座標軸と、同じく 0.8[S] で交差している。
そもそも、空間軸は時間軸と同じ角度で閉じていた。
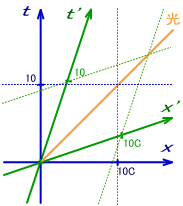
図1.4-8
結局、図1.4-8 の通り45度の光の軌跡を挟んで、時間軸と対称的な目盛とならざるを得ない。
この様に空間軸方向でも、同じ比率で座標の目盛りが間延びしている。この間延びしたS’系の座標を使って距離を測ると、長さが変わって見えることになる。
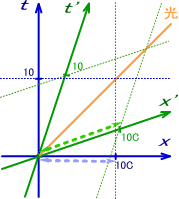
図1.4-9
これがいわゆるローレンツ収縮という現象だ。
あらためて強調すると、運動している物体の長さ測る場合は、両端を”同時刻”に測るしか無いということだ。これは相対性理論と関係なく受け入れなければならない現実だ。そしてS系で測るということは、S’系の時間 t’ ではなく t を使って測るということになる。
1.5 ローレンツ変換
静止系S-移動系S’の間の座標変換式を幾何学的に求めてみよう。このやり方はあまりエレガントとは言えないが、最も実感がわく方法だと思う。
任意の世界点PをS系の座標を用いてP(x,t)とする。
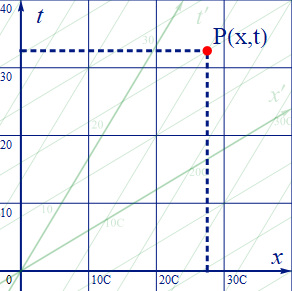
図1.5-1
Pは同時にS’で測るとP(x’,t’)である。そのP点を通るS’系での同一時刻を、以下の様に緑の点線で表し、静止系t軸との交点をTとする。緑の時計はP点における移動系時刻を表示しており、全てP点と同時刻の [t’] を指している。そして青い時計は交点における静止系時刻のTを示している。
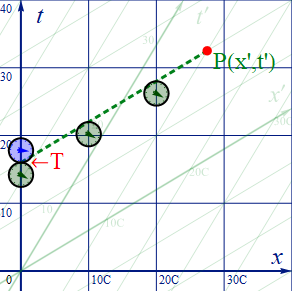
図1.5-2
S系の座標上でT点の高さ(=t座標値)を求る。尚、x軸の1目盛りは光秒単位 ”C” で振られているので、グラフ上で傾きを基に計算する場合、横軸の長さは 1/c倍する必要がある。
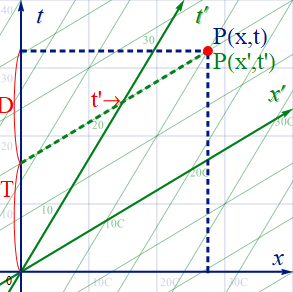
図1.5-3
これに先ほど求めたEq1.5-1に代入すると
同様に、空間軸のx’に関する変換式を求めて見よう。
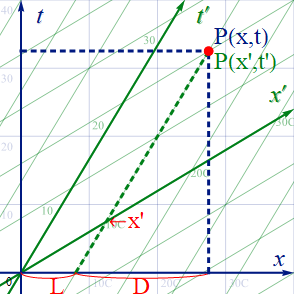
図1.5-4
導出方法はt’の場合と全く同だ。
t’,x’の変換式をまとめて書いておく。これが、かの有名なローレンツ変換の式だ。
また、逆変換式(ローレンツ逆変換式)は
となる。これは、S-S’系の対応関係は、運動方向の左右が逆なだけ、つまり相対速度が+/-の差でしかない。 従って、x、x’と、t、t’を入れ替えて速度をマイナス符号にするだけで、逆変換式を導き出せる。
尚、
1.6 ミンコフスキー時空
これまで、時間軸tは[秒]を単位としてグラフの一目盛は1S(1秒)とか10S(10秒)という様に割り振って説明してきた。この様なやり方は、前述の同時性に関する思考実験の様に、亜光速での運動を、我々の日常からの延長でイメージしやすい。一方、空間軸Xの方は[m]を単位として、グラフ上の一目盛は1光秒(1C)とか10光秒(10C)として説明してきた。
この場合図5-1のように、光の軌跡は45度になる。
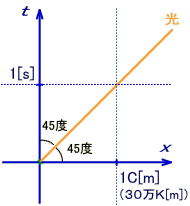
図6-1
ところで、図5-1のように、時間軸をctと書換えても光の軌跡を45度することができる。
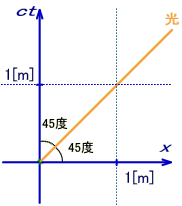
図1.6-2
この座標では、時間軸に相当する縦軸が光速度c[m/s]×t[s]であり、結局ctは[m]という距離の単位になっている。相対性理論では時空をこの座標で表現し、ミンコフスキー時空と呼ぶ。
この場合ローレンツ変換は以下Eq1.6-1となる。
逆変換、つまり移動系座標から静止系座標を知るには
となる。
時間軸に相当するものが距離になってしまったが、空間軸と時間軸のスケールがそろって見通しが良い。前節で幾何学的にな考察時に空間軸を c で割って補正していたが、不要になる。以降、時空はこの”正統派”の表現法であるミンコフスキー時空で表すことにする。
早速ローレンツ変換を使ってみよう。
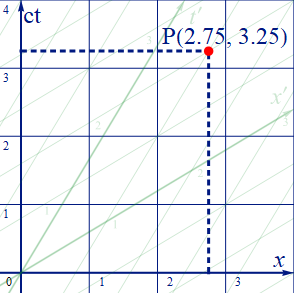
図1.6-3a
上記、図6-3aのP点は静止系:Sの座標で
x: 2.75[m]
ct: 3.25[m] (t=2,75/c≒9.2×10-9[秒])
となる。
この世界点をローレンツ変換(Eq1.6-1)で移動系:S’の座標に読み替えてみよう。
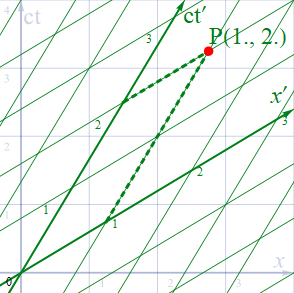
図1.6-3b
電卓や表計算を使ってβ=0.6, γ=1,25として計算すると
x’: 1[m]
ct’: 2[m] (t’=2/c≒6.7×10-9[秒])
となる。
以上、このようにローレンツ変換の公式を得るにいたるまで、『光速度不変の原理』と『相対性原理』以外の仮定が必要とされなかったことを、あらためて強調しておきたい。
付録稿 本編に直接関係は無いが、興味がある方はどうぞ

続き> 特殊相対性理論2 [不変量編]






コメント