特殊相対性理論３ [力学編]

特殊相対性理論２ [不変量編］より続いて、相対論的力学を理解する。特殊相対性理論１および２での解説の通り、距離や時間、さらに速度の定義が変わってしまった。これはニュートン力学の土台が揺らいでいることを意味する。本編ではアインシュタインがいかに、ニュートン力学を作り替えたかを理解し、あの有名な E=mc² を導出してみよう。

3.1 速度の加算

今、v系から見てw系が相対速度 β₂=0.3 で移動しているとする。その v系はｘ系から見てβ₁=0.3で移動しているとする。単純に考えるとx系から見たw系の移動速度はβ₁＋β₂=0.6になりそうなのだが、はたしてどうだろうか？　少し計算してみよう。

まずｖ系原点の軌跡を青いベクトルとしてプロットしてみよう。傾きは当然β₁=0.3だ。長さをv系の単位時刻分としよう。そのためにはv系座標点 [1 0] を逆変換し矢印の終点とすれば良い。さて、このベクトルはβ₁=β₂=0.3としてあるので、v系から見たw系の軌跡とも一致しているはずだ。従って、この青いベクトルをさらに逆変換すればｘ系からみたw系の軌跡が得られるはずだ。その結果を下記、図3.1-1に緑のベクトルでプロットした。

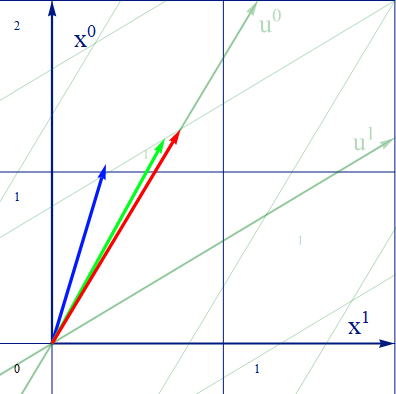
図3.1-1

赤いベクトルは比較用のu系（β=0.6) の軌跡だ。x系時刻１の目盛線との交点の x¹ 値がそれぞれのベクトルの速度に対応している。青ベクトルは0.3、赤ベクトルは0.6であるのに対し、緑ベクトルは少し手前で交差している。この様に結果は0.3+0.3<6となって、単純な加算は成り立っていない。

以下、具体的に計算してみよう。まず、青ベクトル終点の座標は以下の式で与えられる。

\[\small \bf P_b=\gamma_{2}\left(\begin{array}{c} 1&\beta_2\\ \small \beta_2&1 \\ \end{array}\right) \left(\begin{array}{c} 1\\ 0 \end{array}\right) =\gamma_2\left(\begin{array}{c} 1\\ \beta_2 \end{array}\right) \]

この青ベクトル P_b をさらに逆変換すると、緑ベクトル P_g が得られる。

\[\small \bf P_g=\gamma_{1}\left(\begin{array}{c} 1&\beta_1\\ \small \beta_1&1 \\ \end{array}\right) \bf \cdot P_b =\gamma_1\gamma_2\left(\begin{array}{c} 1+\beta_1\beta_2\\ \small \beta_1+\beta_2 \\ \end{array}\right) \]

上記 P_g の成分の（P_g¹/P_g⁰）が緑ベクトルの傾きを示しているので、これが速度加算後の光速度比となる。よって、以下の Eq3.1-1 が速度加算の公式となる。

\[\small \frac{\beta_1+\beta_2} {1+\beta_1\beta_2} \tt \tag{ Eq3.1-1} \]

これにβ₁=β₂=0.3を代入して計算すると、緑ベクトルの光速度比は約0.55であることが分かる。

参考までに、β=0.15として10回ほど加算した結果を以下に示す。

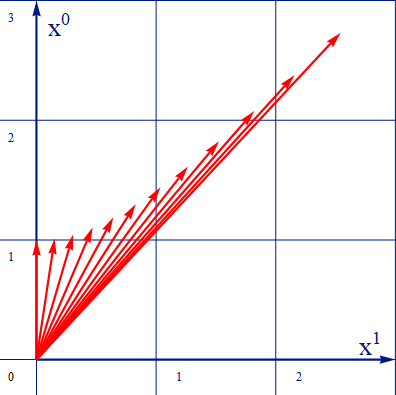
この様に　加算を繰り返すと、速度は光速に対して漸近していくことが理解できる。

3.2 ニュートン力学

ニュートン力学を少し復習しておこう。まず、ニュートンの運動方程式は以下の通り。質点の質量をm₀とし、 x、V、A、P、F はそれぞれユークリッド空間の3元ベクトルで、位置、速度、加速度、運動量、力を表す

\[\small m_0\frac{\text{d}^2 \bf x}{\text{d}t^2} =m_0\boldsymbol{A} =\frac{\text{d} \bf P}{\text{d}t} =\bf F \space,\\ \small \boldsymbol{A}=\frac{\text{d} \bf V}{\text{d}t} \tt \tag{Eq3.2-1} \]

時間ｔは空間とは独立したパラメータで、すべての系で共有されている。

運動エネルギーEと仕事率の関係は以下の通り。

\[\small E=\frac{1}{2} m_0 \bf V^2 \\\downarrow \]

\[\small \frac{d}{dt}(E)=\frac{1}{2}\frac{d}{dt}m_0 (\boldsymbol{A} t \cdot\boldsymbol{A} t) = m_0 \boldsymbol{A} \cdot \boldsymbol{A} t=\boldsymbol{F}\cdot \boldsymbol{V} \tt \tag{Eq3.2-2} \]

つまり、運動エネルギーの時間微分は、仕事率（力と速度の積）となる。

ガリレイ変換

運動方程式は以下のガリレイ変換に対して不変だ。

\[\small \begin{cases}t’ =t\\ \bf x’=x- V\tt t \end{cases} \]

このガリレイ変換の式はは今までのローレンツ変換のでの体裁に合わせ、速度を光速比βで表すとすると、

\[\small \left(\begin{array}{c}t’\\ x^{1′} \\ x^{2′}\\ x^{3′}\end{array}\right)= \left(\begin{array}{c} 1&0&0&0\\ -\beta&1&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}\right)\left(\begin{array}{c}t\\ x^1\\ x^2\\ x^3\end{array}\right) \tt\tag{Eq3.2-3} \]

最初の空間成分をｘとし、[x-t] 平面でこの式を図に表すと、以下の図3.2-1 となる。静止系の座標を青、移動系の座標を緑でうすく表示している。

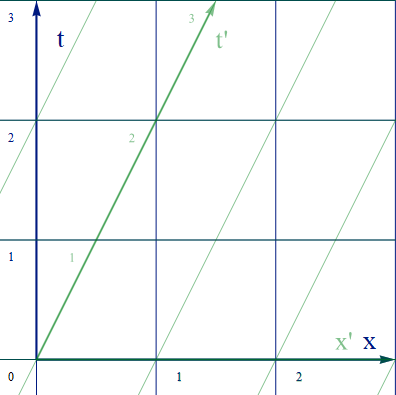
図3.2-1

縦軸が時間で、横軸が空間だ。時間は両系で共通しており、目盛りも一致している。例えば地上が青座標でと移動する電車内が緑座標といったの関係だ。

このニュートンの運動方程式を使った応用例として、質点単振動を考える。

ばねの右端に［　|–VVVVV–(O)　］こんな感じで重りがついており、左端は固定されている。重りは、ばねの張力や反発力で左右に振動する。ばねの自然長からの変位に対しフックの法則により、以下の式の通り、ばねの硬さ k に応じて力Fが働く。右に引っ張った場合の変位を＋u とすると左向き、つまり -F_h が、右に押し込んだ場合は逆向きに反発力として+F_h が生じる。

\[\small F_h=-k\space u \tt \tag{Eq3.2-4} \]

Eq3.2-1とこのEq3.2-3により、以下の微分程式が得られる。

\[\small m_0\space u”(t)=-k \space u(t) \tt \tag{Eq3.2-5} \]

これを解くと、以下Eq2.3-6の質点の単振動の解が得られる。振幅Cは任意の定数となる。

\[\small u(t)=C\space\sin{\sqrt{\frac{k}{m_0}}}\space t \\ \small 周期 T=2\pi \sqrt{\frac{m_0}{k}} \tt \tag{Eq3.2-6} \]

この式に、ばね定数ｋ、質量m₀を指定すると具体的な周期や、加速度が得られる。

例えばm⁰=1[kg], k=（2π)² [N/m]とすると、以下の通り周期Tは１秒となる。

\[\small u(t)=C\space\sin{2\pi}\space t \\ \small 周期 T=1 \tt \tag{Eq3.2-7} \]

さて、『ニュートンの運動方程式 Eq3.2-1 はガリレイ変換で不変である』という意味だが、『どちらかの系で具体的に定数を設定して記述した式、例えば単振動の方程式が、他の移動系系でもそのまま使える』と言うことだ。

このようなガリレイ変換は日常生活に照らし合わせても、しごくもっとものように思える。ニュートン力学では少なくとも速度が光速に対し十分遅い場合、ガリレイ変換で運動方程式は変わりなく成り立つことが検証されている。この後、ガリレイ変換の代わりにローレンツ変換を使った場合の問題点を確認し、ローレンツ変換に対して不変であるような運動方程式を求めよう。

仮想力学実験：ニュートン力学とガリレイ変換

いまX系（静止系）とU系（移動系）の空間位置ベクトルをそれぞれ[x¹,x²,x³] 、 [u¹,u²,u³] とし、 x¹ 、u¹ を系の相対移動方向とする。そしてＵ系の中に実験室があり以下の図の様なばね式の重量計を設置する。図の上下方向がu²軸となる。この重量計は押し下げられるとプラスの重量を、引き上げられるとマイナスの重量を表示をする。質量を1㎏に調節済みの時計を、実験用質点として受け皿に固定しておく。

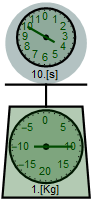
Eq3.2-7の通りこの重量計のばね定数 k＝(2π)²としておき、地表でこの1kgの質点を計ると受け皿の沈み込む変位 u= m₀g/k=0.248405[m]が求まる。(重力加速度 g = 9.80665とした)

逆に宇宙空間でこの重量計に1kgを表示させるためには、受け皿を0.248405[m] 押し下ることが必要になる。

この重量計と重り時計を宇宙船の実験室に設置しよう。以下の図の様に重量計は机に固定しておくが質点の方はu² 軸方向を高さとして、高さ1.5mを中心に上下にゆらゆらと振動している状況を想像してほしい。

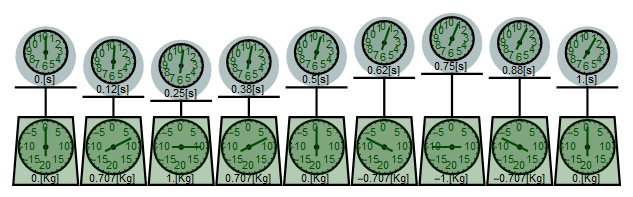
受け皿を0.248405[m] 押し下げて、ぱっとはなす。制動機構を外してあるので、振幅C=0.248405で、Eq3.2-5より得た以下の式により、いつまでも振動する。ばねの自然長位置を1.5とし、変位を u とすると、質点の高さ u2は以下の式で表される。

\[\small u^2(t’)=C\space\sin{2\pi}\space t’+1.5 \\ \small 周期 T=1 \tt \tag{Eq2.3-8} \]

振動している質点位置が、ばねの長さを変えることになる。重量計に表示される重さW_hは、Eq3.2-3のフックの法則を使うと以下の式となる。

\[\small W_h(t’)=-\frac{k}{g} (u^2(t’)-1.5) \tt \tag{Eq3.2-9} \]

力の単位は[N]なので、重力加速度 g=9.80665[m/s²]で割れば重量計に表示される重さが求まる。そしてこれは最大振幅点で±1㎏と表示される。

一方、質点はゆらゆらと振動しているので、ニュートン力学では、以下のような加速度由来の力 F: [F¹,F²,F³] が生じているこのになる。

\[ \small \left(\begin{array}{c} F^1=0\\ F^2=m_0\large\frac{\text{d}^2u^2}{\text{d}t’^2}\small =-4 \pi^2 C \space \sin{2 \pi t}\\ F^3=0 \end{array}\right) \]

この中のF²を、やはり重力加速度 g=9.80665[m/s²]で割れば、受け皿におよぶ加速度由来の荷重 W_mがkg単位で求まる。

\[ \small W_m=-\frac{4 \pi^2 C}{g} \space \sin{2 \pi t’},\\ \small C=\frac{g}{k},\quad k=4 \pi^2\\ \downarrow\\ \small W_m=- \sin{2 \pi t’} \tag{Eq3.2-10}\]

以上をプロットすると図3.2-2、図3.2-3の様になる。x¹/u¹を系の移動方向とし、グラフ上では横軸にとってある。質点は横軸に対し静止している。縦軸は時間ｔ’となる。グラフ上の立ち上がった軸がx²で、質点の振動方向だ。

尚、振動方向u²の目盛りは[m]となっているが、系の移動方向となる横軸u¹の目盛りは[l.s]と表記してある。これは光秒(light second)単位を意味しており、両者のスケールが大きく異なっていることに留意しておいてほしい。

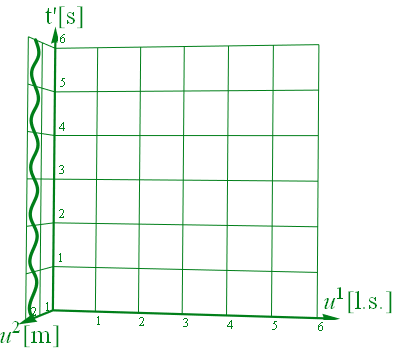
図3.2-2

[t’-u²]面正面から見ると以下の図3.2-3となる。緑の実線は質点の軌跡（位置）を示し、点線は加重W_mだ。

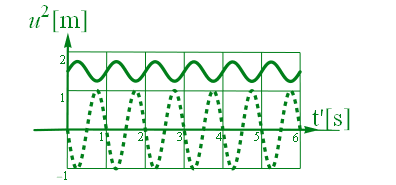
図3.2-3

この場合、単振動の方程式 Eq3.2-5よりEq3.2-6で算出済みだが、質量m₀=1とすると、実験中の重量計のばね定数kは 4π² と逆算できる。つまりU系での実験は正しく設定されており、加速度由来の荷重と、フックの法則由の荷重が一致していることが確認できた。

この実験室系（U系）からはなれて、静止系（X系）から実験を眺めてみよう。Eq3.2-2により質点のU座標位置をガリレイ変換（逆変換）を行い、プロットすればよい。

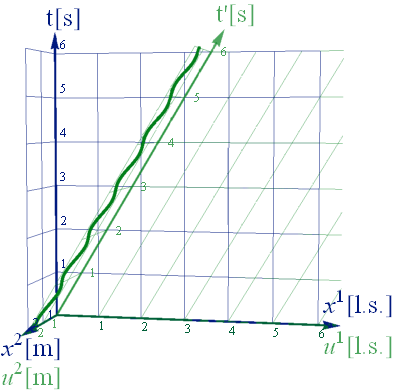
図3.2-4

さて、このX系に変換された質点の座標を基に、ニュートンの運動方程式 Eq3.1-1をあらためて適用してｆより受け皿への荷重量を計算し、質点の軌跡に重ねてプロットしてみよう。

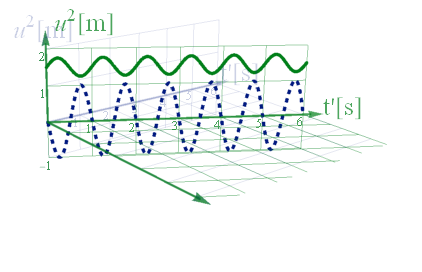
図3.2-5

この通り、U系での実験結果（図3.2-3）と同じものだ。ガリレイ変換後も加速度由来の荷重とフックの法則由来の荷重は一致する。質点の位置を求めるためには速度が関係するがニュートン力学の方程式には加速度と時間しか関係していない。時間がX,U系共通であるので同然の結果だ。

仮想力学実験：ニュートン力学とローレンツ変換

それでは、ガリレイ変換と同じ実験をローレンツ変換で行ってみよう。

下記図3.2-6はU系における質点の軌跡をローレンツ逆変換し、X系にプロットしたものだ。ガリレイ変換に似ているが振動が遅くなっている様に見える。

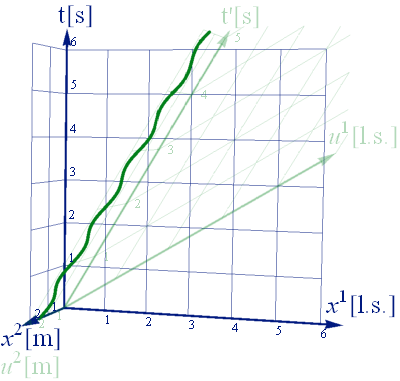
図3.2-6

これはU系の時間軸が t=t’/γ の関係式で間延びしていることによるもので、Eq2.3-7 をX系での軌跡を表すように修正すると、以下のEq3.2-11の通りとなる。

\[\small x^2(t)=C\space\sin{2\pi}\frac{1}{\gamma} t+1.5 \\ \small 周期 T=\frac{1}{\gamma} \tt \tag{Eq3.2-11} \]

次にこの質点の軌跡 Eq3.2-11 に対して、加速度由来の荷重を求めてみよう。

\[ \small W_m=- \frac{1}{\gamma^2}\sin{2 \pi \frac{1}{\gamma}t } \tag{Eq3.2-12}\]

この式を青の点線で質点の軌跡に重ねると図3.2-7 にとなる。尚、u²軸は移動方向と直交しているのでローレンツ変換で影響はない。加えて質点の振動によりu²方向に最大２π[m/s]の速度が生じるが、これによるローレンツ収縮や時間の遅れなどは十二分に小さく、ニュートン力学の議論の範疇では考慮不要として無視する。

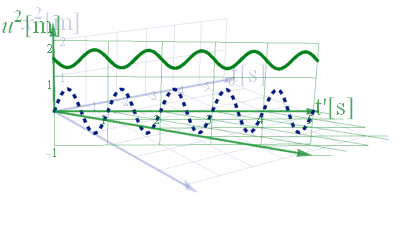
図3.2-7

困ったことに、荷重が1㎏より小さくなってしまった。計算すると、1/γ² より、0.64kgだ。一方重量計の受け皿の沈み込み量 d はローレンツ変換でも変わらなく、0.248405[m]なので重量計は 1kg を表示していなければならない。

この様に、ローレンツ変換でニュートンの運動方程式に基づく加速度由来の荷重と、フックの法則由来の荷重は一致しない。つまりニュートンの力学をローレンツ変換で成り立つように根本から修正する必要がある。なぜなら、特殊相対性理論１ [ローレンツ変換編]の議論よりガリレイ変換は亜光速では成り立たないことが明白となっているからだ。

3.3 物理量の4元化

振り返るとミンコフスキー時空では、力学の土台と言える距離の定義が時間と併せて4元化されて、ローレンツ変換に対して不変量となっている。したがって運動方程式に登場する運動量も、時間由来の成分と併せて4元化することが理にかなっていると思われる。

そこでアインシュタインは、ニュートン力学における運動方程式を、以下のように修正した。

\[\small m_0\frac{\text{d}^2 \bf x}{\text{d}\tau^2} =m_0\boldsymbol{\alpha} =\frac{\text{d} \bf p}{\text{d}\tau} =\boldsymbol{ f }\space,\\ \small \boldsymbol{\alpha}=\frac{\text{ d}\bf v}{\text{d}\tau} \tt \tag{Eq3.3-1} \]

x 、v、 p、f、αはミンコフスキー時空における4元ベクトルで3元ベクトルと区別するために小文字を使う。また、τは移動する質点にくくりつけられた系の時間、つまりＵ系の時間軸 u⁰と同じものだ。ただし運動方程式上、どちらの系でも共通に使えるパラメータとして使い、固有時間と呼ばれる。

4元速度

ミンコフスキー時空の4元座標を成分とする位置ベクトル：ｘ＝[x⁰, x¹, x², x³]とした場合、以下の通り固有時間 τ で微分したものを4元速度と定義する。

\[\small \boldsymbol{v}=\frac{\text{ d}\boldsymbol{ x}}{\text{d}\tau} \tt \tag{Eq3.3-2} \]

この τ は以下の図の様に前述の仮想実験に出てきた質点に張り付いた時計と思えばよい。

図3.3-1

例えば実験室の座標が[x⁰, x¹, x², x³]であり、、質点には瞬時瞬時に速度に対応した移動系座標[u⁰, u¹, u², u³]が括りついていると考えられる。以下は実験室に静止している場合だが、U系はX系と同じ座標系が張り付いている。赤い点線のベクトルで示す通り、時空上を１秒後に同じ空間位置に移動する。

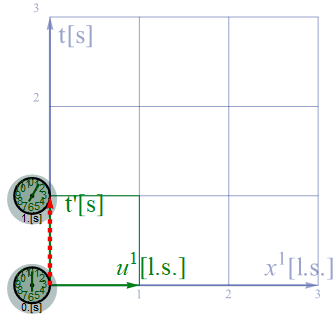
図3.3-2

質点が亜光速で運動している場合、以下の様に大きく斜交したU系が張り付いていると考えられる。この例では質点の移動速度V¹を光速度比0.8とした。

この重り時計が1秒を表示する点は以下の通りで、赤い点線のベクトルは１固有時間秒におけるに時空上を移動距離を示す。

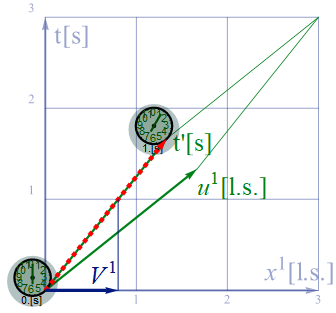
図3.3-3

青い矢印はニュートン力学における実験室系時間1秒後の3元座標 x¹ での移動距離 d を示し、ｄ＝V¹ t=0.8c ≒2.4×10⁸[m]。

この様に各ベクトルはそれぞれの単位時間での時空の移動距離を表しているので、これらは速度ベクトル考えてよいだろう。

これをもう少し詳しく整理してみると、以下の3元速度ベクトルと4元速度ベクトルの関係が得られる。

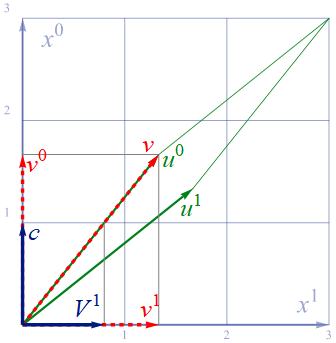
図3.3-4

数式で書くと、4元速度の時間成分 v⁰ は Eq3.3-2 より

\[ \small v^{0}=\frac{dx^{0}}{d\tau} =\frac{c \space dt}{dt}\frac{dt}{d\tau} =\gamma\space c , \\ \small \gamma=\frac{1}{\sqrt{1-\beta^2}}, \quad \beta=\frac{V^1}{c} \]

この関係より、v¹ と V¹ との関係が図より理解でき、併せて書くと

\[\small \begin{cases}v^0=\gamma c \\ \small v^1=\gamma V^1 \end{cases} \tt \tag{Eq3.3-3} \]

今回 β=0.8であるので、γは約1.7となる。

Eq3.3-3 より、質点が静止している場合、V¹=0、γ=0　であるため、質点の4元速度 vは光速度 c となる。これは図3.3-2 よりも分かることだ。

物質は静止していても4元速度はゼロにはならないという事が理解できた。

4元運動量

Eq3.3-3の両辺に\(m_0 \) を掛けて4元運動量との等式とする。\(\\ \)

\[ \begin{cases} \small p^{0}=\gamma\space m_0 \space c \\ \small p^{1}=\gamma\space m_0 V^{1} \end{cases} \tt \tag{Eq3.3-4} \]

ここで、相対論的な質量を\(\small m \equiv \gamma \space m_0\) と定義すると、4元運動量は以下の通りニュートン力学に近い記述が可能となる。\(\\ \)

\[ \begin{cases} \small p^{0}=m \space c \\ \small p^{1}= m \space V^{1} \end{cases} \tt \tag{Eq3.3-5} \]

4元力

3元力の定義を以下の様にEq3.3-4での相対論的質量: m を基にした運動量を使って定義し直す。

\[ \small F^1=\frac{d p^{1}}{d t} \tt \tag{Eq3.3-6} \]

ここでこの相対論的質量を与えられた質点を加速し続けると、速度がどうなのかを確認しておこう。γは以下の式の通り3元速度Vの関数と言える。したがってF¹を一定に固定してV¹について解けば良い。

\[\small F^1=\frac{d}{d t}\left(\gamma m_0 V^1\right)=\frac{d}{d t}\left(\frac{1}{\sqrt{1-\left(\frac{V^1}{c}\right)^2}}m_0 V^1\right) \]

ここでm₀はニュートン力学の質量なので以下の様に A¹=F¹/m₀ と置き換えられる。

\[\small A^1=\frac{d}{d t}\left(\gamma V^1\right)=\frac{d}{d t}\left(\frac{1}{\sqrt{1-\left(\frac{V^1}{c}\right)^2}} V^1\right) \]

この加速度一定の微分方程式を V¹=0 の初期条件で速度について解くと

\[\small V^1(t)=\frac{cA^1 t}{\sqrt{c^2 +(A^1)^2 t^2}} \tt \tag{Eq3.3-7} \]

定数を簡単のため[A¹=1,c=1]と与え横軸にｔを取り速度V¹をプロットすると

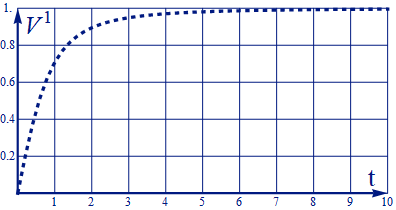
図3.3-5

この様に質量に掛かるγが増えて、（c=1とおいた）光速度に漸近し、超えることはできない。

Eq3.3-5より、4元力の空間成分と3元力の関係が以下の通り求められる。

\[\small f^1=\frac{d p^{1}}{d t}=\frac{ d p^1}{d t}\frac{d t}{d \tau}=\gamma F^1 \tt \tag{Eq3.3-7} \]

E=mc²の導出

それでは4元力の時間成分はどうなっているのか？

不変距離 s² (特殊相対性理論２ [不変量編］Eq2.3-21)の定義より以下の等式が成り立つ。

\[\small \begin{cases}s^2= c^2 d\tau^2\\ \small s^2=\eta_{\mu\nu}dx^\mu dx^\nu =\eta_{\mu\nu}v^\mu v^\nu d\tau^2\end{cases} \\ \]

これにより、時間成分と空間成分の関連式が得られる。4元速度の時間成分と空間成分は独立していない。

\[ \small (v^0)^2-(v^1)^2=c^2 \\ \tt \tag{Eq3.3-8} \]

この関連式を、積の微分の公式を使って\(\small \tau \)で微分し、さらに第二項の速度微分を4元加速度に置き換えておく。　\(\\ \)

\[ \small 2v^0 \frac{dv^0}{d\tau}-2v^1\frac{dv^1}{d\tau}=0\\ \downarrow \\ \small 2v^0 \frac{dv^0}{d\tau}-2v^1\alpha^1=0 \]

第二項を右に移項し両辺にm₀ を掛ける。

\[ \small{v^0 \frac{d \space m_0 v^0}{d\tau}=v^1 m_0\alpha^1} \\ \downarrow\\ \small{v^0 \frac{dp^0}{d\tau}=v^1f^1} \\ \downarrow\\ \small{c \frac{dp^0}{d\tau}=V^1f^1} \]

左辺をγと座標系時間 t による微分の項に変形し、γを移項すると、右辺はニュートン力学での仕事率（力と速度の積）の定義 Eq3.2-2 と等しくなる。

\[\\ \small{\gamma \frac{d (c p^0)}{dt}=V^1f^1} \]

↓

\[ \small{\frac{d (c p^0)}{dt}=V^1F^1}\\ \\ \tt \tag{Eq3.3-9} \]

これによりcp⁰は、積分定数: C 分の任意性は残るものの、ニュートン力学でのエネルギー: Eに相当していると言うことになる。尚、右辺は3元量のすべてを記述する場合、 V^1:3・F^1:3 の様に、3元ベクトルの内積の形になる。

アインシュタインは積分定数Cを０として、p⁰=mc の関係式より以下の様にエネルギーを定義した。

\[\small E=cp^0+C=mc^2 \tt \tag{Eq3.3-10} \]

これが有名なアインシュタインのエネルギーの公式だ。相対論的の質量 \(\small m\) に関しては、以下のように静止質量に相対速度 \(\small \bf v\) をパラメータとする係数 \(\small \gamma\) が掛かっている。尚、今回は簡単のため \(\small \bf v\) は \(\small V^1\) である。

これが有名なアインシュタインのエネルギーの公式だ。相対論的の質量 m に関しては、以下のように静止質量 m₀ に相対速度 v をパラメータとする係数 γ が掛かっている。尚、今回は簡単のため v は V¹ である。

\[\small mc^2=\gamma m_0 c^2=\frac{1}{\sqrt{1-\left(\frac{v}{c}\right)^2}} m_0 c^2 \tt \tag{Eq3.3-11}\]

エネルギーと速度の関係を確認するために図3.3-5に、さらにEq3.3-9で V¹F¹ を積分したものと、Eq3.3-11でのmc²（両者は当然一致する）を重ねてプロットしてみよう。

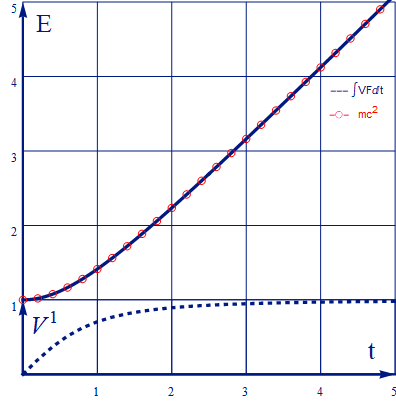
図3.3-6

v<<c の条件で以下の近似が成り立つ。

\[\small \frac{1}{\sqrt{1-\left(\frac{v}{c}\right)^2}}= 1+\frac{1}{2}\left(\frac{v}{c}\right)^2\]

したがって、低速で動く質点のエネルギーは以下のように近似できる。

\[\small E= m_0 c^2+\frac{1}{2}m_0v^2 \\ \tt \tag{Eq3.3-12}\]

第二項がニュートン力学で認知されていた運動エネルギーである。低速である加速初期、最初の赤丸３個め程度までは、ニュートン力学なじみの放物線を描いていることに対応する。一方第一項は隠れていた質量でのみ決まるエネルギーであり、アインシュタインにより初めて、その存在の可能性が見いだされた。これはエネルギーのグラフが底上げされて１から始まっていることに対応する。前述の式の変形過程で述べた通り、積分定数分の不定性があるため、この第一項を差し引いてエネルギーが０から始まる様に定義することも可能だが、アインシュタインはこのまま残した。

そしてその後、この質量が持つ静止エネルギーは、原子力という形で実証され、誰もが知る有名な公式の一つとなったことは衆知のことだ。