信号処理の基礎数学１[直交変換編］

計算機代数ノート
2021.07.18

信号処理はアナログの波形をデジタルで扱い携帯電話やデジタルテレビ等の核心的な技術となっている。そう、携帯電の中では実際に複素指数関数や確率論等当の数式をコンピュータが高速に計算しているのだ。つまり『携帯電話やテレビは数学でつながっている！』と言って過言ではないだろう。その数学の論理的基盤はフーリエ変換やラプラス変換、複素関数など、なかなか面白い分野にわたっている。

一般的に数値処理に特化した対話型の言語（Matlab,Scilab）で信号処理のアルゴリズムを検証し、C言語等で実装するという開発の流れが多いと思う。そこで信号処理に必要となる数学を数値処理ソフトで実例を示しながら解説するという形式を取ろうと思う。また数式の理解を補助するために数式処理ソフト（MathematicaやMathematica等）も取り入れようと思う。従って本稿は計算機代数（CAS-Lab)の範疇でもある。

数学のおさらい

数値処理ソフトを使って、以降必要となる最低限の数学のおさらいをしておこう。とりあえず以下Scilabで解説するので環境を構築し以下の　”–>”に続くコマンドをコピペ＆実行しながら読み進めることをお勧めする。

ベクトル・行列

Scilabの例
数と数の間をスペースで空けるか、カンマで区切ると横向き、列方向の要素となる。セミコロンで区切ると縦向き、行方向の要素。

2行3列の行列A
-->A=[1 2 3; 4 5 6]　  
 A  =
 
    1.    2.    3.  
    4.    5.    6. 

3行2列の行列B
-->B=[7 10; 8 11; 9 12]
 B  =
 
    7.    10.  
    8.    11.  
    9.    12.  

掛け算（内積）
Aの列数とBの行数が同じであること。

-->C=A*B
 C  =
 
    50.     68.   
    122.    167.

複素平面と定数π、e、虚数単位i

Scilabの例
cilabでは他の変数と区別するために頭に%を付ける。

円周率π
-->%pi
 %pi  =
 
    3.1415927  

自然乗数の底e
-->%e
 %e  =
 
    2.7182818

虚数単位i
-->%i
 %i  =
 
    i   

虚数単位iは複素平面で左に90度（=π/2）回転させる演算子だ
-->C=[%i^0; %i^1; %i^2; %i^3; %i^4; ]
 C  =
 
    1.   
    i    
  - 1.   
  - i    
    1.

複素平面にプロットすると、以下の様に左から右へ90度ずつ回転している。実数軸が横、虚数軸が縦だ。

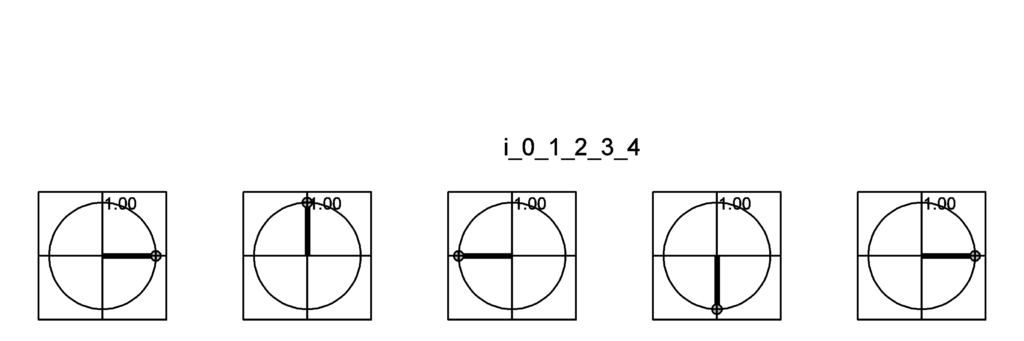
もう少し細かく回そうとすると複素指数関数の出番だ。

\[ e^{i\pi t} \]

ｔをパラメータとして0～πを4分割して表示してみよう。

時間ベクトルｔを生成する。 [・]’は行列の要素を縦横転置する演算。

-->t=[0:4].'/8   
 t  =
 
    0.     
    0.125  
    0.25   
    0.375  
    0.5    

以下 C は e の指数部で 2πit をあらしている。最終値はπiとなる。 D が演算結果だ。
-->C=2*%pi*%i*t
 C  =
 
    0           
    0.7853982i  
    1.5707963i  
    2.3561945i  
    3.1415927i

-->D=%e^C
 D  =
 
    1.                      
    0.7071068 + 0.7071068i  
    6.123D-17 + i           
  - 0.7071068 + 0.7071068i  
  - 1. + 1.225D-16i   

clean関数で小さな数を消そう。    
-->clean(D)
 ans  =
 
    1.                      
    0.7071068 + 0.7071068i  
    i                       
  - 0.7071068 + 0.7071068i  
  - 1.

このDを図にすると、以下の様に45度（=π/４）ずつ複素平面を左向きに回っている。

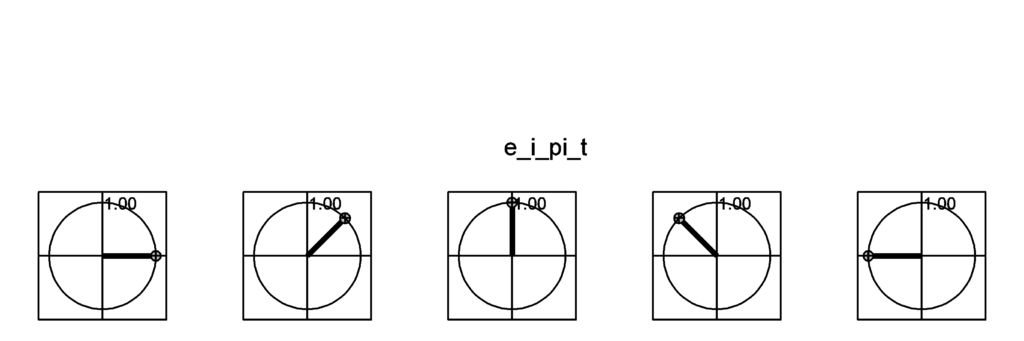
ｔの刻みをもう少し細かくすると、もっとスムースに回るはずだ。
ところで最後に行き着いた先は ‘-1’ だった。つまり、

\[ -1=e^{i\pi } \]

となる。

余談だが、実はこれが有名な『数学の定理の中で最も美しい』と言われるオイラーの等式（Euler’s identity）だ。この事例でいうと一回転の途中がたまたま -1 だったようにも見えるが・・・。

あと、必要となる数学の基礎知識は微積分程度だろうか。それではおさらいはこの程度にして先に進もう。

1.1 直交基底

『次の連立方程式を解け！』…　中学校あたりの数学の問題だったろうか。

\[\small \left\{\begin{array}{c} 5=1 x_1+2 x_2\\\\ \small 6=3 x_1+4 x_2 \end{array}\right\} \]

答えは、

\[\small x_1=-4, \quad x_2=9/2 \]

だ。当時めんどくさくも頑張って解いていたような記憶がある。じつはこの答えは数式処理でらくして回答させたのだが。
これを行列・ベクトルの式であらわすと

\[\small \left(\begin{array}{c} 5\\ \small 6 \end{array}\right) = \left(\begin{array}{c} 1&2\\ \small 3&4 \end{array}\right) \left(\begin{array}{c} x_1\\ \small x_2 \end{array}\right) \quad \rightarrow \quad \left(\begin{array}{c} x_1\\ \small x_2 \end{array}\right)= \left(\begin{array}{c} -4\\ \small 9/2 \end{array}\right) \]

これを組み合わせ [5 1 2], [6 3 4] として、当然[1 2 3], [4 5 6] の様ないろいろな組み合わせに対して答えが存在する。( ただし、[1 2 3]と[1 2 3]を何倍かしたものとの組み合わせはは同じ式となるので答えは存在しない )

これらを行列の一般型で書くと

\[\small y=a\cdot x \]

要素で書くと

\[\small \left(\begin{array}{c} y_1\\ \small y_2 \end{array}\right) = \left(\begin{array}{c} a_{11}&a_{12}\\\small a_{21}&a_{22} \end{array}\right) \left(\begin{array}{c} x_1\\ \small x_2 \end{array}\right) \]

この場合『ｘベクトルをａの行ベクトルでｙに変換する』式と見ることができる。つまり変換用の行ベクトルを組み合わせて任意のｙが生成できる。

信号処理的に言うと、『ｘを入力信号とし、変換ベクトルの組み合わせで任意の出力ベクトルｙを合成できるとなる』となる。逆は真でだろうか？　つまりｙを任意に取り、かつ変換ベクトルも任意の場合、入力ベクトルを決定できるのだろうか？

勿論、それは真だ。つまりｙ、ａの方を任意に決めてｘを求める事が出来る。連立方程式が解けるからだ。

ここでａは任意なので以下の様に選んでも問題無いはずだ。

\[\small a =\frac{1}{\sqrt{2}} \left(\begin{array}{c} \color{blue}{1}&\color{blue}{1}\\ \small \color{red}{1}&\color{red}{-1} \end{array}\right) \]

そうするとこの場合の方程式は

\[\small \left(\begin{array}{c} 5\\ \small 6 \end{array}\right) =\frac{1}{\sqrt{2}} \left(\begin{array}{c} \color{blue}{1}\\ \small \color{red}{1} \end{array}\right) x_1+ \frac{1}{\sqrt{2}} \left(\begin{array}{c} \color{blue}{1}\\ \small \color{red}{-1} \end{array}\right) x_2 \]

となり、連立方程式を解くと

\[\small x_1=11/\sqrt{2}, \quad x_2=-1/\sqrt{2} \]

が解となる。

ところでこの場合、実はいちいち連立方程式を解かないで済む、非常に簡単なｘの求め方が存在する。以下の様にｙの成分と右辺の列ベクトルとの積和を求めて見よう。

\[\small \frac{1}{\sqrt{2}} \left(\begin{array}{c} 5\times\color{blue}{1}\\ \scriptsize +\\ \small 6\times\color{red}{1} \end{array}\right)=11/\sqrt{2}, \quad \frac{1}{\sqrt{2}} \left(\begin{array}{c} 5\times\color{blue}{1}\\ \scriptsize +\\ \small 6\times\color{red}{-1} \end{array}\right) =-1/\sqrt{2} \]

いきなり解が求まった。何だかキツネにつままれたようだ。

実は、秘密はａは直交基底を並べたユニタリー行列と言われる特殊な行列であることにある。

連立方程式の解を求めるということは逆行列を求めることに等しい操作だ。ところがユニタリー行列は転置（行と列を入れ替える）し、さらに複素共役を取ると逆行列と等しい、つまり

\[ a^{-1}=^t\bar{a}\quad \]

という便利な行列なのだ。この場合 a は実数なので、以下の様にａを転置で縦横ひっくり返して内積（つまり積和演算）を取るだけで簡単にｘを求められたわけだ。

\[ x=a^{-1}\cdot y=^t a\cdot y \]

先ほどの計算もこの式を利用していた。ただ、２倍になったりしているのでもう少し行ａ選び方を工夫しなければ完全なユニタリー行列といえない。

以下、アダマール変換でもう少しこの方法を検討してみよう。

1.2 直交基底

連立２次から４次に拡張してみよう。以下の様に直交基底を行ベクトルとする。

続く　＞[1.3 アダ-マール変換]　＊ニューアル中（完了するまでは続きは下記旧バックアップサイトの参照となる）

１．直交変換
　１．１　直交基底
　１．２　アダマール変換
　１．３　離散コサイン変換（ＤＣＴ）
　１．４　離散フーリエ変換（DFT)
　１．５　フーリエ変換・フーリエ級数との関係
　１．６　δ関数列による離散化（アナログからデジタルへ）

２．線形システム
　２．１　畳み込み積分
　２．２　直交変換と固有値解析
　２．３　フラプラス変換・ｚ変換
　２．４　フィルターの基礎

３．ランダム過程
　３．１　乱数

Appendix
　行列の分類メモ

Post Views: 6

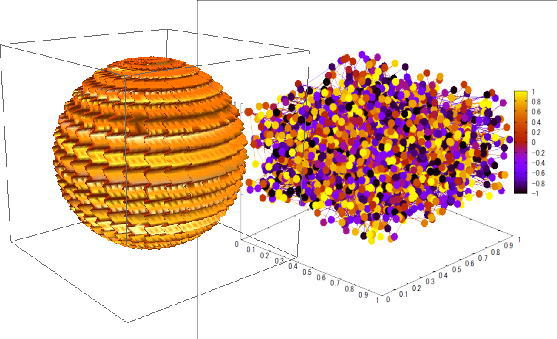
コメント

タイトルとURLをコピーしました