特殊相対性理論１ [ローレンツ変換編] に続き、本篇ではユークリッド空間とミンコフスキー時空を比較しながら座標変換における不変量とは何かを理解する。
2.1 座標変換
先々の準備のため、ローレンツ変換の式を行列形式にしておこう。
ローレンツ変換の式（特殊相対性理論 1 ミンコフスキー時空 Eq1.6-1 ）をあらためて書くと
\[\small
\begin{cases}
ct’= \gamma (ct-\large\frac{v}{c}\small x)\\
\small
x’=\gamma (x-vt)
\end{cases} , \\ \small
\small \quad\gamma=\frac{1}{\sqrt{1-\beta^{2}}},
\quad\beta=\frac{v}{c} \tt\tag{Eq2.1-1}\]
この式は以下の様に行列の積として記述することができる。
\[
\small
\left(\begin{array}{c}ct’\\ x’\end{array}\right)=\left(\begin{array}{c}\gamma&-\gamma\beta \\
-\gamma\beta&\gamma
\end{array}\right)\left(\begin{array}{c}ct\\x\end{array}\right)
\tt\tag{Eq2.1-2}
\]
ここで、ct は時間軸、ｘは空間軸だが、空間の方は本来3次元であるから 空間座標は（x1 x2 x3 ）で表される。それに加えて時間軸 ct をx0 と表すと、時空点は4次元空間における座標（x0 x1 x2 x3 ）で表すことができる。
\[
\small
\left(\begin{array}{c}x^{0′} \\x^{1′}\\x^{2′} \\x^{3′} \end{array}\right)=\left(\begin{array}{c}\gamma&-\gamma\beta &0 &0 \\
-\gamma\beta&\gamma &0 &0 \\
0 &0 &1 &0 \\
0 &0 &0 &1
\end{array}\right)\left(\begin{array}{c}x^0\\x^1\\x^2\\x^3\end{array}\right), \\ \small \quad\gamma=\frac{1}{\sqrt{1-\beta^{2}}},
\quad\beta=\frac{v}{c}
\tt\tag{Eq2.1-3}\]
ここで右辺を行列 部をL と定義する。
\[\small \bf L\it=\left(\begin{array}{c}
\gamma&-\gamma\beta &0 &0 \\
-\gamma\beta&\gamma &0 &0 \\
0 &0 &1 &0 \\
0 &0 &0 &1
\end{array}\right)\]
\[\bf \small u=L\cdot x
\tt\tag{Eq2.1-4}\]
そして、静止系座標を位置ベクトルx 、移動系座標を位置ベクトルu とする（本来x’ とする方が自然だが、計算機代数の解説との関連で本稿ではu を採用した）と、ローレンツ変換は以下の様な行列とベクトルの積による線形変換の式で表すことができる。注１）
次元数をｎとして成分のみで書くと
\[\small
u^\mu=\sum_{\nu=0}^{n-1} L^\mu_{\space\nu}\space x^\nu,\quad \mu=0,1,\cdot\cdot,n-1
\tt\tag{Eq2.1-5}
\]
上下に出てくる指標 ν は積和を示しているものみなし、Σ記号を 省略すると
\[\small
u^\mu=L^\mu_{\space\nu}\space x^\nu
\tt\tag{Eq2.1-6}
\]
これはアインシュタインの縮約規則などと呼ばれ、数式が見やすくなる。
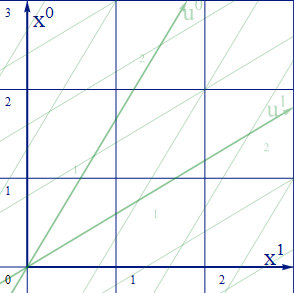
尚、移動系との相対速度は x1 のみに限って議論しており、ローレンツ変換で影響のない空間成分は[u２ u３ ]=[x２ x３ ]となっていることが理解できる。
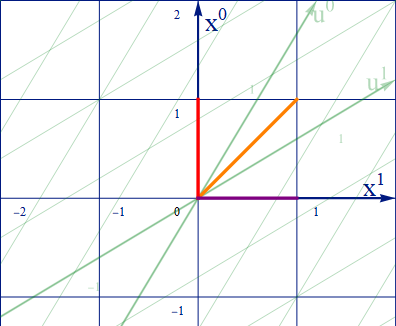
以降、以下の図の様に、時間軸は ct, ct’ に代えて x0 , u0 の様に表す。
図2.1-1
次にEq2.1-4の式でxとuを入れ替えてみる。右辺は行列とベクトルの積なので、L は逆行列L -1 となる。これがローレンツ変換の逆変換式だ。
\[\bf \small x=L^{-1}\cdot u\space,\\ \\
\bf \small L^{-1}=\left(\begin{array}{c}
\gamma&\gamma\beta &0 &0 \\
\gamma\beta&\gamma &0 &0 \\
0 &0 &1 &0 \\
0 &0 &0 &1
\end{array}\right)
\tt\tag{Eq2.1-7}\]
ローレンツ変換における速度に関する係数の符号が逆転しているだけだ。これはすれ違う相手の系が左から右に移動するのか、右から左に移動するかの差でしかないことが確認できる。
注１）ここで本稿における手抜きのための注意点をいくつか： 成分を横書きにより、行ベクトルとして表記したものを、行列に掛ける場合は列ベクトルに転置されていたものとして扱う。
・行列の積であることを明示するために内積の”・”記号を使う
2.2 ユークリッド空間との比較
ニュートン力学では、空間を（x1 x2 x3 ） など3次元の直行直線座標（デカルト座標）で表し、時間は空間と独立した１個の変数ｔなどで表す。そして時間 t は全宇宙の全ての質点に共通のものである。
全ての質点が３次元のデカルト座標で表現出来る以上、この物理空間・全宇宙はユークリッド空間にはめ込まれており、全宇宙共通の時間に合わせて、物理現象が起きていると考えた。
もちろん物理現象を記述する上で、他の曲線座標系、例えば楕円座標や球座標などが都合が良い場合は、技法としてデカルト座標以外を用いることを行う。
『ユークリッド空間や時間は誰が作ったのだろうか？ 神様です。 いやいや最初から在ったんでしょう。 云々かんぬん』と言うふうに、『物理以前の自明な概念であり、あえて言えば神学や哲学の範疇である』と、ニュートンも時間、空間の概念を天下り的に受け入れていた様だ。
この『ユークリッド空間でこの世は出来ている』という概念は、ニュートンならずとも、ごくごく自然なもので、中学校の数学などでデカルト座標やグラフの授業を受けると、あっと言う間にこの世の中はユークリッド空間だと悟ってしまう。別に中学校の先生は、この世の中はユークリッド空間できているなどとは、教えていたとは思わないのだが。
以降、私たちはユークリッド空間という名前は忘れても、この概念の中で全てを考えるようになる。
しかし、相対性理論や量子力学を知るうちに、この物理空間に対する概念は、実生活上の便法でしかなかったことに、気付かされる。
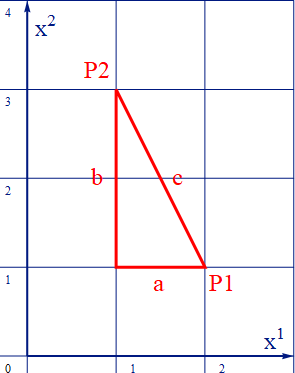
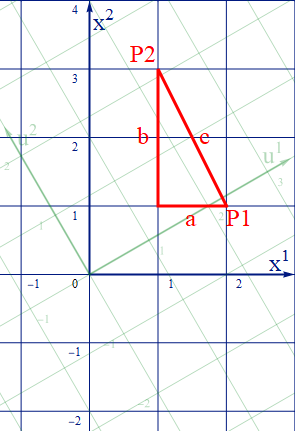
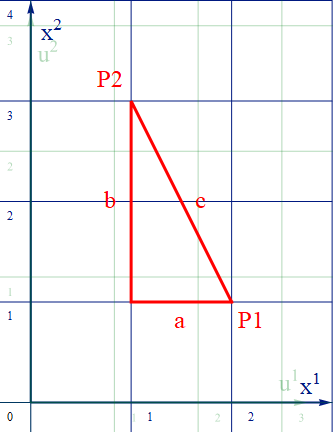
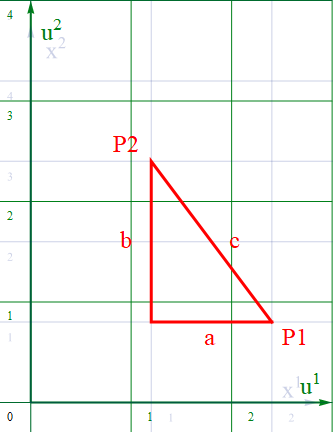
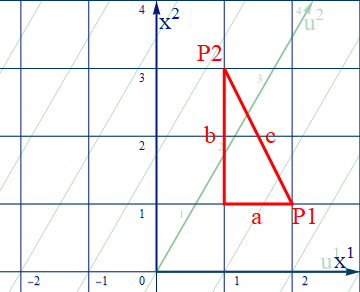
ユークリッド空間では直交直線座標（ここでは [x1 -x2 ] 平面としよう）を用いると、直角三角形で斜辺の長さｃにピタゴラスの定理:c2 =a2 +b2 が成り立つ。ここでｃの両端をp1、p2とすると線分ｃはp1、p2間の距離と言える。そして直交辺の a、b は線分ｃの座標成分と見ることができる。
図2.2-1
したがって、二次元直直線交座標における任意の2点間の線分をベクトル Δx とし、その成分を [Δx1 Δx2 ] とすると、2点間の距離:ｓには s2 =(Δx1 )2 +(Δx2 )2 が成り立つ。ベクトルの内積: Δx .x 1 )2 +(Δx2 )2 なので s2 = Δx .x x 2 = Δx .x
座標の平行移動変換
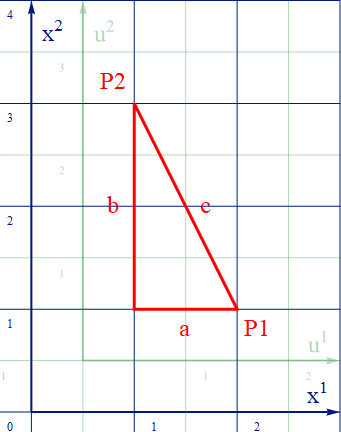
次に、ごく当たり前の話をあえてしてみよう。図2.2-1の座標系をx系とし、このx系から以下の図2.2-2aの様に少し平行移動した別の座標系Uを用意する。移動量をβ とすると、変換式はもちろん u =x –β となる。以下の図ではβ =[+0.5,+0.5]とした。
図2.2-2a
この新たな座標のu系で線分ｃを測り直し、その成分を [Δu1 Δu2 ] とすると、数式を記述するまでも無く、 s2 =(Δu1 )2 +(Δu2 )2 =(Δx1 )2 +(Δx2 )2 が成り立つことが理解でき、u系における線分ｃのs2 も５となることが分かる。
図2.2-2b
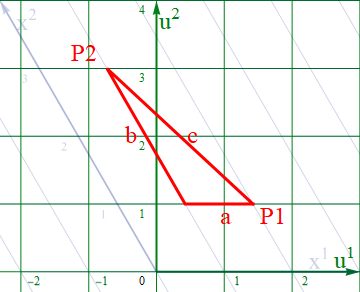
座標の回転変換
座標を回転させるてみるとどうなるか？先ほどの平行移動の場合と異なり、ベクトルの成分は変わって見える。
座標回転による変換：x <->u を行列の演算で表すと、以下のEq2.2-8の様になり、Eq2.2-9のローレンツ変換ど同じ、線形変換の式で表すことができる。
回転変換
\[\bf \small
\begin{cases}
\bf u=C\cdot x\\ \\
\bf x=C^{-1}\cdot u
\end{cases},\quad C=\left(\begin{array}{c}cos\beta&-sin\beta\\ sin\beta&cos\beta\end{array}\right)\tt\tag{Eq2.2-8}
\]
ローレンツ変換
\[\bf \small
\begin{cases}
\bf u=L\cdot x\\ \\
\bf x=L^{-1}\cdot u
\end{cases},\quad L=\left(\begin{array}{c}\gamma&-\gamma\beta\\ -\gamma\beta&\gamma\end{array}\right) \tt\tag{Eq2.2-9}\]
βは座標系の回転角（右回り）である。C の逆行列C-1 はローレンツ変換と同様にβの符号を反転させれば良い。尚、この章における C -1 や L -1 は、基底行列（変換先の系を張るための基底ベクトルを行列として束ねたもの）となる。以下内容を読み進む前に、こちら でベクトル空間における基底ベクトルの概念を理解しておいた方が良いかもしれない。
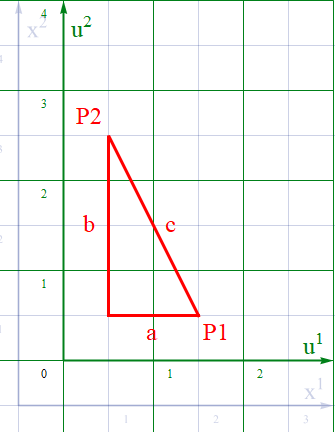
いまβ=-30度として元のｘ系の座標を左に30度回させてみよう。図2.2-3a は回転させた座標をu座標系とし、背後に緑線で薄く表示してる。
図2.2-3a
このu系に乗り換えてみると、先ほどの線分はどう見えるか？ 以下図2.2-3bの通りだ。
図2.2-3b
うす青く表示してある旧x系上の各点は、全て右に30度回転されている。このu系における線分ｃの成分より距離 s2 を計算する以下のように 5 となり、両者のs2 は一致する。
\[\small \Delta u\cdot \Delta u=\begin{bmatrix}\frac{1}{\sqrt{2}} & \frac{3}{\sqrt{2}} \end{bmatrix}
\cdot\begin{bmatrix}\frac{1}{\sqrt{2}} & \frac{3}{\sqrt{2}} \end{bmatrix}=\tt 5 \]
つまり2点間の距離は座標の回転変換に対して不変量となっている。
この様に座標の回転変換は、視点を変えることであり、目の前にある物体を見るとき、真っすぐに見ようと首をかしげて見ようと、その長さという物理量は変わらないということだ。
同様に座標を上下左右に平行移動させても視点が移動しただけで長さという物理量が変わることはない。
ローレンツ変換と回転変換の類似性
以上で、ローレンツ変換と回転変換を具体的に比較できるようになった。実は虚数角を使って回転変換するとローレンツ変換になる。ただし虚数時間で時空を扱う必要があるのだが、もし先に進む前に興味がある場合は以下も参照のこと。
特殊相対性理論 [付録稿] 虚数角回転によるローレンツ変換
擬ユークリッド空間でのローレンツ変換は、ユークリッド空間での回転変換によく似ているといわれている。なんと回転の変換式に、虚数の回転角を入れるだけでローレンツ変換と等価となるとのこと。 なかなか興味深い話である。
2.3 計量
物理学的には長さを測定する上で、メートル法を使ってもヤードポンド法を使っても、読み替えが定義されていれば物理法則に影響はない。つまりヤードポンド法でニュートン力学を書き上げることは可能だ。
この後相対性理論を理解するうえで、曲がった空間を記述するため直交直線座標以外の座標系を学ぶ必要が出てくる。そこで、座標軸が斜交したり、異なる目盛（スケール）を持つ座標への変換どのようになるのかを調べてみよう。
座標のスケール変換
スケール変換、逆変換の式を以下の様に定義しよう。
\[\bf \small
\begin{cases}
\bf u=C\cdot x\\ \\
\bf x=C^{-1}\cdot u
\end{cases},\quad C
=\left(\begin{array}{c}\beta_1&0\\0&\beta_2\end{array}\right)\tt\tag{Eq2.3-10}
\]
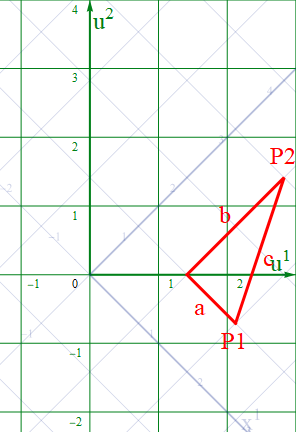
例えば、β =[β1 β2 ]=[6/5 4/5]とすると、以下の図2.3-4aの様に、u系座標の１目盛りがx系に比べて u1 , u2 それぞれ [5/6 5/4] に伸縮している。
図2.3-4a
u系に乗りかえて、x系を見てみよう。
このu系に乗りかえて長さを測ると縦横のスケールが変わってしまい、以下の図2.3-4bの様に3角形がずんぐりした形に変形してしまった。
図2.3-4b
このu系における線分ｃの成分の値は [-6/5 8/5] なので、s2 =100/25=4となり、 x系でのs2 =5と異なってくる。そこで目盛りの読み替え表の様なものが必要になる。手っ取り早くはスケール補正用の対角行列を考えよう。これを以下の様にs2 を計算する前に Δu に掛けて補正すればよさそうだ。（半分に縮んだ定規で測った測定値は倍になっているので、測定値を半分にしなければならないという理屈。これはCの逆行列に等しい）
\[\small
\Delta \mathbf{x}=\left(\begin{array}{c}\small \Delta x^1\\
\small \Delta x^2\end{array}\right)=\left(\begin{array}{c}1/\beta_1&\small 0\\
\small 0&1/\beta_2\end{array}\right)
\left(\begin{array}{c}\small \Delta u^1\\
\small \Delta u^2\end{array}\right)
\]
この補正後のΔu’ を自乗してｓ2 を求めてみよう
\[\small
\Delta s^2=\Delta \mathbf{x}\cdot \Delta \mathbf{x}\\=
\left(\begin{array}{c}\large\frac{5}{6}&\small 0\\
\small 0&\large\frac{5}{4}\end{array}\right)
\left(\begin{array}{c}\small \Delta u^1\\ \\
\small \Delta u^2\end{array}\right)
\cdot
\left(\begin{array}{c}\large\frac{5}{6}&\small 0\\
\small 0&\large\frac{5}{4}\end{array}\right)
\left(\begin{array}{c}\small \Delta u^1\\ \\
\small \Delta u^2\end{array}\right)\\
\]
展開すると
\[\small
\Delta s^2=(\frac{5}{6})^2 (\Delta u^1)^2+(\frac{5}{4})^2 (\Delta u^1)^2
=\frac{25}{36}\frac{36}{25}+\frac{25}{16}\frac{64}{25}=5
\]
と、s２ が一致し、うまく補正できた。
この補正行列を以下の様に予め自乗しておくと便利だ。
\[
\small
\mathbf{g}=\left(\begin{array}{c}\large\frac{5}{6}&\small 0\\
\small 0&\large\frac{5}{4}\end{array}\right)
\left(\begin{array}{c}\large\frac{5}{6}&\small 0\\
\small 0&\large\frac{5}{4}\end{array}\right)
=\left(\begin{array}{c}\large\frac{25}{36}&\small 0\\
\small 0&\large\frac{25}{16}\end{array}\right)
\tt\tag{Eq2.3-11}
\]
以下の様にΔu
\[
\small
\Delta s^2＝ \Delta \mathbf{u}\cdot\mathbf{g }\cdot \Delta \mathbf{u}
\tt\tag{Eq2.3-12}
\]
この行列 g は計量（Metric)と呼ばれ、相対性理論で重要な役目を果たすことになる。
座標のせん断（座標の傾け）変換
図2.3-5aの様x2 軸に対しu2 軸を30度右に傾けてみよう。この様な変換を行列の積の形で表すと、以下の通りとなる。縦方向の目盛りの高さは両系とも同じだ。
\[\bf \small
\begin{cases}
\bf u=C\cdot x\\ \\
\bf x=C^{-1}\cdot u
\end{cases},\quad C
=\left(\begin{array}{c}1&tan(-\beta) \\0&1\end{array}\right)\tt\tag{Eq2.3-13}
\]
図2.3-5a
u系に乗りかえてみると図2.3-5bの通り、x系が左に30度傾いて線分ｃは間延びして見える。
図2.3-5b
この様に座標を傾けると先ほど議論したスケール変換が生じていることになる。ちょっと複雑になりそうだが、早速計量を求めてみよう。
x系における線分ｃをベクトルΔｘ 、u系ではΔu で表す。平行移動でs2 は不変だから線分の始点（P1)を原点に移動させたと考えると、以下の Eq2.3-14 の様に座標の逆変換式がそのまま適用できる。
\[\small
\Delta s^2= \Delta \mathbf{ x }\cdot\Delta \mathbf{ x }=(\mathbf{ C }^{-1}\Delta \mathbf{ u })\cdot (\mathbf{ C }^{-1}\Delta \mathbf{ u })\\
\\ \small
\tag{Eq2.3-14}
\]
せん断変換（Eq2.3-13）のC-1 を代入し展開すると
\[\small
=(\Delta u^1)^2+\Delta u^1\Delta u^2 tan(\beta) +\Delta u^2\Delta u^1 tan(\beta)+ (1+ tan^2(\beta))(\Delta u^2)^2
\]
Eq2.3-12と見比べると、
\[\small
s^2= \left(\begin{array}{c}\Delta u^1\\\Delta u^2\end{array}\right)^t\left(\begin{array} {c}1&tan(\beta)\\
\small tan(\beta)&1+ tan^2(\beta)\end{array}\right)
\left(\begin{array}{c}\Delta u^1\\ \Delta u^2\end{array}\right)
\]
よって、計量 g は以下の通りとなる。
\[\small
\mathbf{ｇ}=\left(\begin{array} {c}1&tan(\beta)\\
\small tan(\beta)&1+ tan^2(\beta)\end{array}\right)
\]
この計量の形態より、角度βに対して計量は奇関数として変化し、変換、逆変換では計量が異なることが理解できる。そもそも座標変換による長さの補正のために計量が必要となったのであるから、当然と言えば当然だ。
同じことを回転変換に試してみよう。計量は
\[\small
\Delta s^2= (\mathbf{ C }^{-1}\Delta \mathbf{ u} )^{\boldsymbol{\cdot} 2}
\small =\begin{bmatrix}\left(\begin{array}{c}cos\beta&sin\beta\\ -sin\beta&cos\beta\end{array}\right)
\left(\begin{array}{c}\Delta u^1\\\Delta u^2
\end{array}\right)
\end{bmatrix}^{\boldsymbol{\cdot}2}\\
\small =(cos^2 \beta+sin^2 \beta)(\Delta u^1)^2+(cos^2 \beta+sin^2 \beta)\Delta u^2)^2\\
\small =(\Delta u^1)^2+(\Delta u^2)^2
\\ \small
\tag{Eq2.3-15}
\]
注）記述短縮のため肩にかかった”・2 ”は、ベクトルの内積自乗を表す
よって、求める計量は以下の通り、単位行列と同じものになる。
\[\small
\mathbf{ｇ}=\left(\begin{array} {c}1&0\\
\small 0&1\end{array}\right)
\small
\tag{Eq2.3-16}\]
注目すべきはEq2.3-15より理解できる様に、せん断変換と異なり計量はβの大きさや、符号によらない。よって変換、逆変換のどちらからでも同じ計量となり回転角度に区別が無い。このことは平行移動変換でも言える。これも回転変換や平行移動変換で長さが変わらないという事の裏返しの表現と言えよう。
それでは、ローレンツ変換での計量はどうなっているのか？同じことを試してみよう。
\[\small
\Delta s^2= (\mathbf{ L }^{-1}\Delta \mathbf{ u} )^{\boldsymbol{\cdot} 2}
\small =\begin{bmatrix}\left(\begin{array}{c}\gamma&-\gamma\beta\\ -\gamma\beta&\gamma\end{array}\right)
\left(\begin{array}{c}\Delta u^1\\\Delta u^2
\end{array}\right)
\end{bmatrix}^{\boldsymbol{\cdot} 2}\\
\small =\gamma [(1+\beta^2 )\Delta (u^0)^2-4\beta u^0 u^2 +(1+\beta^2 )\Delta ( u^1)^2]
\]
これより、
\[\small
\mathbf{ｇ}=\gamma\left(\begin{array}{c} 1+\beta^2 &2\beta\\
\small 2\beta & 1+\beta^2 \end{array}\right)
\]
注）記述短縮のため肩にかかった”・2 ”は、ベクトルの内積自乗を表す
残念ながらこの算出法による計量は光速度比βに依存している。これでは、せん断変換の計量の様に、β=0の系を基準に、変換先の長さを補正する場合の計量だ。しかし速度は二つの系間の相対的なものであったので、基準の長さを定めるための絶対静止系の様な特別な系が必要になる。
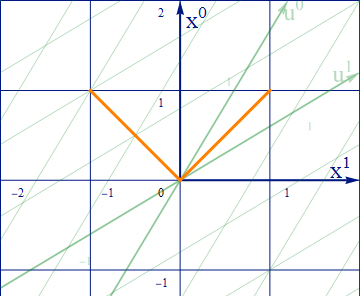
光速度不変の原理に立ち戻ってみよう。x系で原点から発せられた光は以下の様に3次元空間を球面状に広がっていく。
\[\small
(x^1)^2+(x^2)^2+(x^3)^2=(x^0)^2
\]
この等式を（x1 -x0 ) 平面でとらえると、以下の図の様に左右に伸びる線分となる。
図2.3-6a
この等式を少し変形すると、以下の通りとなる。
\[\small
(x^0)^2-(x^1)^2=0
\]
一方、x1 方向に相対的に移動するu系でも光速度不変の原理により以下が成り立つ。
\[\small
(u^0)^2-(u^1)^2=0
\]
従って。少なくとも光球面を記述する方程式として、x系-u系間に以下の等式が成り立つ。
\[\small
(x^0)^2-(x^1)^2=(u^0)^2-(u^1)^2=0
\small
\tag{Eq2.3-17}
\]
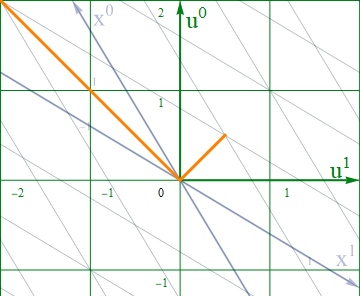
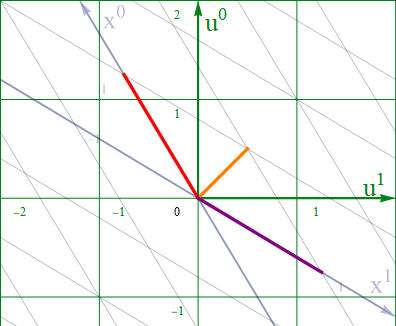
このx系上の線分をローレンツ変換してみると、以下の通りu系図上の±45度線上にマップされており、Eq2.3-17の等式は、一応成り立っていることが確認できる。
図2.3-6b
それではほかの線分はどうだろうか？ 以下の図でx系上では（赤、オレンジ、紫）の線分の(x0 )2 -(x1 )2 はそれぞれ（ 1、0、-1 ）となる。
図2.3-7a
これらをローレンツ変換すると以下の様に赤、オレンジ、紫の線分となり、ベクトルの成分で言うと、[ 1.25 -0.75]、[0.5, 0.5]、[-0.75 1.25]となる。
図2.3-7b
これらの (u0 )2 -(u1 )2 を計算するとそれぞれ（ 1、0、-1 ）となってx系のそれと一致している。このことよりミンコフスキー時空の(x1 )2 -(x2 )2 は不変量の様であり、ローレンツ変換で大きさが保たれていることが推定できる。そこでミンコフスキー時空の自乗距離 s2 を以下の通り定義しよう。
\[\small
\begin{cases} s^2=\eta_{\mu \nu} x^\mu x^\nu \\ \\ \scriptsize あるいは\\
s^2=\bf x\cdot \eta \cdot x
\end{cases}
,\quad \eta=\left(\begin{array}{c} 1&0\\0&-1\end{array}\right)
\small
\tag{Eq2.3-18}
\]
この定義に基づいてあらためて計量を求めてみよう。
\[\small
\Delta s^2= (\mathbf{ Ｌ }^{-1}\Delta \mathbf{ u}) \cdot \eta\cdot (\mathbf{ Ｌ }^{-1}\Delta \mathbf{ u})
\\
\small =(\Delta u^0)^2-(\Delta u^1)^2
\\ \small
\tag{Eq2.3-19}
\]
よって求める計量は以下通りとなる。
\[\small
\mathbf{ｇ}=\left(\begin{array}{c} 1 &0\\
\small 0 & -1 \end{array}\right)
\small
\tag{Eq2.3-20}
\]
この計量は速度に依存せず、したがってローレンツ変換、逆変換でも同じものとなり、Eq2.3-15、Eq2.3-16のユークリッド空間における回転変換と同じ形式を得ることができた。
\[\small 距離の定義 \small \tag{Eq2.3-21}
\]
ユークリッド空間
\[\small
s^2=\delta_{\mu \nu} x^\mu x^\nu,\quad
\mathbf{\delta}=\scriptsize\left(\begin{array}{c} 1 &0\\
\small 0 & 1 \end{array}\right)\\ \\
\scriptsize 回転変換での計量: \small\space \mathbf{g}=\mathbf{\delta}
\]
ミンコフスキー時空
\[\small
s^2=\eta_{\mu \nu} x^\mu x^\nu,
\quad\small\mathbf{\eta}=\scriptsize\left(\begin{array}{c} 1 &0\\
\small 0 & -1 \end{array}\right)\\ \\
\scriptsize ローレンツ変換での計量: \space\small\mathbf{g}=\boldsymbol{\eta}
\]
ミンコフスキー時空は、上記の様にユークリッド空間の距離の定義を少しひねってあることにより、擬ユークリッド空間とも呼ばれる。
2.4 不変量
この結果より、ベクトル A （例えば2点間の微小距離を示す変位ベクトル）があったとして、ユークリッド空間でデカルト座標におけるベクトルの大きさ（の2乗）を得るためには、気楽に A・A とできた（なぜなら計量が計量ｇ ＝δ であり、これは単位行列なので省略できる）が、ミンコフスキー時空の場合は計量を省略すると A・A ＝(A1 )2 +(A1 )2 となってしまい不変量ではなくなってしまう。
ミンコフスキー時空でのベクトル大きさの2乗 (A1 )2 -(A1 )2 を得るためには、以下の様にA1 の符号（つまり空間成分）を反転させた裏(?)ベクトルの様なものを利用すると便利だ。裏表を区別するために添え字を下げて裏ベクトル Ai としよう。
\[\small
\begin{cases} A^i=[A^1 \space +A^2]\\ \small
A_i=[A_1 \space -A_2]
\end{cases}
\tt \tag{Eq2.4-1}
\]
そうすると、このベクトルA の大きさ s は縮約規則を使って以下の様に記述できる。
\[\small
s^2=A_i A^i\space
\tt \tag{Eq2.4-2}
\]
裏ベクトルを正しく定義すると、以下の様に表ベクトルの頭に事前にミンコフスキー時空の計量を掛けておいたものだ。
\[\small
A_i=g_{ij}A^j\space,\\ \small
g_{ij}=\eta_{ij}=\left(\begin{array}{c}
1&0 \\ \small
0&-1
\end{array}\right)
\tt \tag{Eq2.4-3}
\]
これにより、以下の様な不変量の記述が可能となる。
\[\small
A_i A^i=g_{ij}A^jA^i=s^2
\tt \tag{Eq2.4-4}
\]
表ベクトルは座標変換時に同じ変換を受けるので反変ベクトルと呼ばれ、裏ベクトルは逆変換を受けるので共変ベクトルと呼ばれる。座標変換時の順方向と逆方向の差は相対速度の符号の差でしかなく、空間成分の符号を変えるという事は変換の順・逆方向を変えることと同じだ。
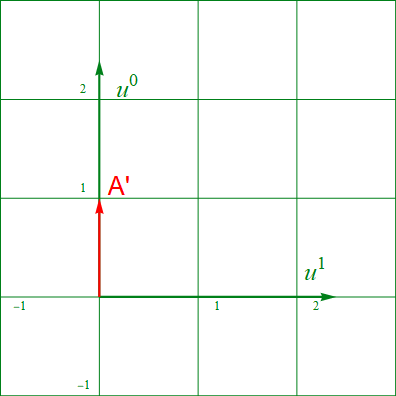
具体例を示そう。以下図2.4-1におけるベクトル A’ はU系において原点に静止している質点の単位時間の変位ベクトルを表している。空間方向の成分は０であり、時間方向に単位時間１の大きさを持つ。この物理量を仰々しく『単位時間変位ベクトル』とでも呼ぶことにしよう。
図2.4-1
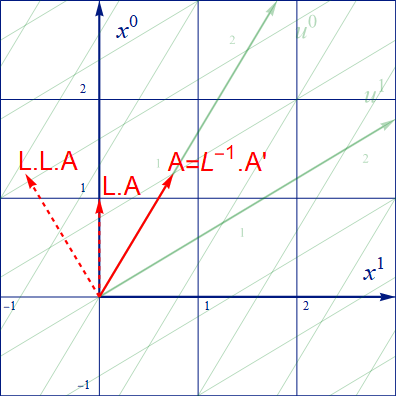
U系はX系に対し x1 方向に光速度比 β=0.6 で移動しているとする。この単位時間変位ベクトルをX系から観察すると、図2.4-2の通り、緑の u0 座標軸に重なったベクトル A となって観測される。先端の座標は [1.25 0.75] だ。
このベクトルは元の A’ をローレンツ逆変換したものとなり、ベクトルと行列の積で表すと、
\[\small
\bf A=L^{-1}\cdot A’
\]
となる。あるいは成分で書くと、以下の通り。
\[\small
\ A^i=(L^{-1})^i_{\space j}\space A^{j\prime}
\]
この右端のベクトルを表ベクトルとしよう。そうすると定義により裏ベクトル gA の先端の座標は左右対称の位置の [1.25 -0.75] となる。
図2.4-2
次にこの表ベクトル Ai をローレンツ変換してみよう。つまり以下の右の式の通り L.A を計算すると結果 [1 0] であり、真ん中の点線で示したベクトルとなる。これはU系（図2.4-1) における元の A’ に戻っている。
\[\small
A^i=(L^{-1})^i_{\space j}A^{j\prime} \space \leftrightarrows \space A^{i\prime}=L^i_{\space j}A^j
\tt \tag{Eq2.4-5}
\]
Eq2.4-5は座標変換（図2.4-1⇔図2.4-2）のルールと同じで、反変性のベクトルだ。
さらにローレンツ変換を行う（つまり L.L.A を計算する）と左端の先端の座標が [1.25 -0.75]の点線のベクトルを得るが、裏ベクトル gA と同じ位置だ。したがって Ai =[A ] をローレンツ変換すると真ん中のベクトルに戻るが、 Ai =[L.L.A ]はは以下の様に逆変換によって真ん中のベクトルに戻る。
\[\small
(L^{-1})^i_{\space j}A_i=\bf L^{-1}\cdot L\cdot L\cdot A\\ \small
= L\cdot A=A’
\tt \tag{Eq2.4-6}
\]
これはEq2.4-5のルール（座標変換と同じ変換というルール）の中に存在しない。表ベクトルの場合A’ を得るためには座標変換と同じくL を掛けるが、裏ベクトルの場合は座標変換の逆のL-1 を掛けている。
逆から考えると、『元のベクトル A’ を座標ごと逆方向に変換したら、右端のA となった。同時にA の裏ベクトルは符号が反転した位置に発現した。これは元の A’ を順方向に変換した位置となる。この様に裏ベクトルは座標変換とは逆になるので共変性のベクトルである』と、言える。
一方、裏・表ペアの積は以下の様に元のA’ に戻してスケールを合わせた状態で大きさを求めていることが理解できる。
\[\small
A_i A^j=g_{ij}A^i A^j\\ \small
=\eta_{nm}(L^{-1})_i^{\space n}(L^{-1})^m_{\space j}A^i A^j \\ \small
=\eta_{nm}(L^{-1})_i^{\space n}A^i \space (L^{-1})^m_{\space j}A^j \\ \small
=\eta_{nm}A^{n\prime} A^{m\prime}=s^2\quad \quad\quad
\tt \tag{Eq2.4-7}
\]
行列の演算で書くと
\[\small
A_i A^i=\bf [(g)\cdot A]\cdot A \quad \quad \quad\\ \small
\quad \quad \quad \small =[ (L^{-1}\cdot\space\boldsymbol{\eta}\space \cdot L^{-1})\cdot A]\cdot A \space \\
\small
\quad \space \space =A \cdot L^{-1}\space\cdot\boldsymbol{\eta}\space \cdot L^{-1}\cdot A \\ \small
=A’ \cdot\space\boldsymbol{\eta} \space\cdot A’=s^2
\tt \tag{Eq2.4-8}
\]
ところで、複素数 a+bi の場合、裏複素数といえる共役複素数 a-bi (虚数部の符号が反転している！）を利用し、裏・表を掛けて絶対値の2乗 (a+bi)(a-bi) を得るが、それと似たような関係と言えるかもしれない。
テンソル
ところで、A に対して別の反変ベクトルB を持ってきてTij =Ai Bj とし、２×２＝４の成分を持つ量を作ることができる。持ってきてと書いたが、同じ座標点に別の量が重ねて定義できるとしての話だ。
例えばスカラー量Eがx系内に分布していたとして、その x で微分された量 \(\small [\partial E(x)/\partial x^i]\) は共変ベクトルとなる。なぜなら\[\begin{bmatrix}\large\frac{\Delta E'(u)}{\Delta u^j} \end{bmatrix}\small=(L^{-1})^i _j\begin{bmatrix}\large\frac{\Delta E(x)}{\Delta x^i} \end{bmatrix}\] で理解できるように、座標位置の変位が分母に入っているため、x->u の変換にローレンツ逆変換が必要となるからだ。
このAi Bj の組見合わせ（直積ⓧを取るという）をテンソルと呼ぶ。両方の添字が上付きなので反変テンソルと呼ばれる。反変ベクトルと共変ベクトルの組み合わせてAi Bj することもできる。この場合添字は上下なので混合テンソルと呼ばれる。当然Ai Bj とすれば共変テンソルだ。Ai Bj の場合、添字を合わせて縮約する（内積を取る）とスカラーとなり、これも座標変換で大きさが変わらない不変量になる。
反変ベクトルを微分した量\(\small \frac{\partial A^i}{\partial u^j}\)は上記のスカラー量微分の議論より混合テンソルとなる。従って、演算子であるが\(\small 1/ \partial u\)は共変ベクトルとして扱うことが妥当となる。
一般的に言うと添字が1つの場合ベクトルとなり、2つ以上となるとテンソルと呼ぶが、座標変換により各成分に共変性か反変性のどちらかを持つことがが必要条件となる。
＊もう少し詳しい具体例などは 一般相対性理論：反変ベクトルの平行移動 を参照のこと。
Post Views: 9
コメント