量子力学の初歩

===注意！　以下執筆・編集中であり誤記多数===

量子力学の超入門であり統一理論に進む前に必要となる最低限の知見を得られること目標としよう。

1 量子とは

1.1 プランク定数

溶鉱炉内で高温となった鉄は、広範囲の波長を持つ光を発している。プランクは温度 Tから発せられる光の持つエネルギーの強度が、波長によりどのように分布するかを表す、以下の『プランクの輻射式』を発見した。

\[\small E_{\lambda}=\frac{2 \pi c^2 h}{\lambda^5 e^{\large \frac{c h}{k \lambda T}}-1},\\\scriptsize h=6.6256×10^{-34} [J\cdot s] \]

ｃは光速、ν は光の周波数、そしてｋはボルツマン定数。h は新たに導入されたプランク定数で6.6256×10^-34 [J・s]である。

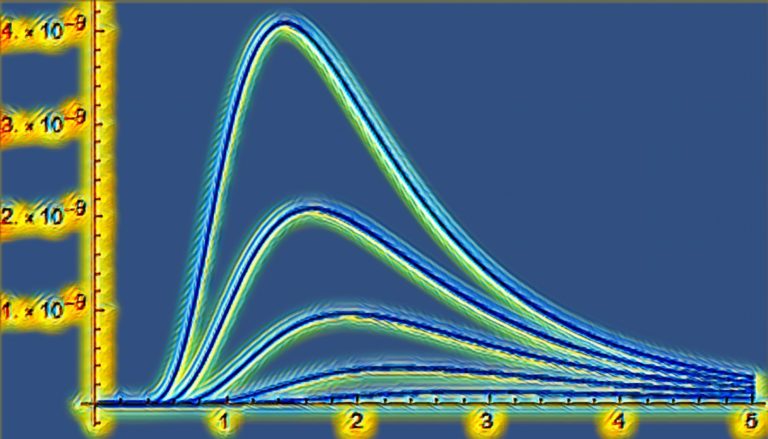
この式を使って温度毎にどのようなカーブを描くか、プロットしてみよう。以下の図は上から絶対温度：T=2000度から、最下位のグラフの1000度までを、250度間隔で計算したものだ。

横軸が波長：λで10^-6m単位で、縦軸はその波長に対するエネルギー密度：E_λを表す。そして各温度毎のエネルギーの総量は当時知られていたボルツマンの黒体輻射の法則

\[ E=\int^{\infty}_{0} E_{\lambda} d\lambda=\sigma T^4 \]

を再現させる。

この様にプランクの輻射式は実験値を正しく表し、他の法則とも矛盾は無いのだが、そこからは非常に小さくはあるがエネルギーがとびとびの値となることを意味した。周波数 ν の光の持つエネルギーは以下の様に hv の整数倍の値しかとれず、従って hv の半分とかは許されない。

\[ E_{\lambda}=n h \nu \]

プランクは当時、このとびとびになることを心良くは思っていなかった様だ。その頃の常識では物理量は連続的であり、エネルギーが離散的に表されていることは、理論にケチがついているように感じていたのかもしれない。

1.2 アインシュタインの光量子仮説

アインシュタインはこの離散的なエネルギーの定義は、黒体輻射という限られた物理現象を表す式ではなく、より根源的な光のエネルギー定義であるねではと考えた。つまり、光はhvのエネルギーを持つ粒子であり、ｎはその粒子の個数を表しているとの解釈だ。

\[ E= h \nu \small \tt \tag{Eq1.2-1} \]

当時の物理学者の間ではヤングによる干渉実験や、マクスウェルの方程式により、光（電磁波）は波として定式化されていた。しかしこの光量子仮説は光電効果をうまく説明で出来るとして受け入れられ、光は波の性格に加え粒子の性質をも持つ物理実態＝『量子』として物理学で認知されるようになった。

プランクの輻射方程式が1900年、アインシュタインの光量子仮説は1905年に発表された。そして特殊相対性理論も1905年に発表されている。つまり1905年にアインシュタインは二つのエネルギーの定義を世に示したと言える。それは特殊相対性理論：E=mc²と、この光量子仮説：E=hν だ。私個人の感想となるが、この二つはアインシュタインの頭の中でつながっていたのだろうか？まさに不世出の大天才だと、あらためて思う。

アインシュタインは光量子の運動量も以下の通り導き出した。

\[ p=h/ \lambda \small \tt \tag{Eq1.2-2} \]

そしてコンプトンにより光量子と電子間の衝突によりエネルギーと運動量がニュートン力学と同様に保存されることが実験で確かめられた。

尚、プランク定数ｈは２πで割った \(\small \hbar=h/(2\pi)\)で利用されることが多く、この場合運動量とエネルギーはそれぞれ波数ｋ, 角速度ωを使って以下の様に定義できる。

運動量：

\[\small p=\frac{h}{\lambda } =\frac{2\pi \hbar}{\lambda}=\hbar k ,\\\scriptsize \hbar=1.0545\space 10^{-34}[J\cdot s] \small \tt \tag{Eq1.2-3} \]

エネルギー：

\[\small E= h \nu =\hbar \omega \tt \tag{Eq1.2-4} \]

2 シュレディンガー波動方程式への道のり

量子のエネルギーの式：Eq1.2-3と運動量の式：Eq1.2-4より、シュレディンガーにより量子の波動方程式が定式化されることになるが、それに至る経緯をもう少し解説しよう。

2.1 ド・ブロイ波

ド・ブロイは光子が波と同時に粒子であるとすると、当時粒子として信じられていた電子は、逆に波の性質も持ち合わせているのではないか？という仮説を提案した。

当時水素原子は、点状の狭い範囲に⊕電荷を持ち電子の2000倍ほどの質量持つ原子核と、その周辺に一定の広がりを持った⊖電荷の電子で構成されていることが、実験により分かっていた。さらに原子は電磁波（光）を吸収したり放出したりしており、放出された電磁波が原子に種類によりそれぞれ固有のスペクトル（波長の位置と強度）を示していた。

長岡半太郎は土星のリングの様に電子が原子核の周りを回転してクーロン力と釣り合っているというモデルを提唱した。しかし電磁気学的に回転により電子は電磁波を放出してエネルギーを失うので、あっという間に原子核に落ち込んで張り付いてしまうことになる。

そこにボーアは『原子の中には電子のエネルギー準位の異なる安定軌道が複数あり、それらの軌道上にあると電子は回転によるエネルギーを失わない。軌道間の遷移でエネルギー準位の差分に相当する電磁波エネルギーの吸収・放出が起きる』というモデルを提案した。かなりなこじつけと開き直りの様におもえるのだが、このモデルは実験の結果をうまく説明できた。ただ、安定軌道とは何なのかは棚上げにのままだ。

その後ド・ブロイは安定軌道とは原子核周囲の円軌道に電子の定常波が出来ているのだという解釈を提案した。つまり原子の周りにある電子は回転する粒子ではなく、波としてふるまい、その波長をλとすると定在波が存在し得る円軌道の半径ｒは以下の式で表すことができる。

\[ 2\pi r=n \lambda \]

ｎは自然数。以下は n=6 の例だ。

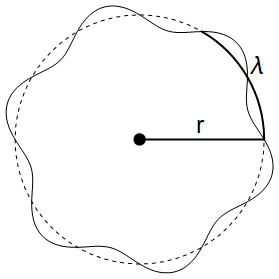
これがボーアの安定軌道の正体であるとの主張だ。さらにド・ブロイは粒子の振る舞いを波動の観点で記述した波動力学の存在を提唱した。これを受けシュレディンガーが具体的に波動方程式を導出し、ド・ブロイが提唱した波動力学が具現化された。波動方程式とはあの有名なシュレディンガー方程式だ。

2.2 シュレディンガー方程式の導出

波動方程式の一般形

波動は時間と空間を合わせてとらえる必要がある。

つまり以下の様に空間の一点を指定して波が時間軸ｔにより、どの様に変化するか？と、

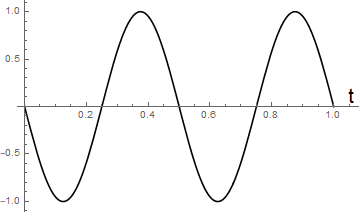
以下の様に、同時刻に空間軸ｘ上に波がどのように分布しているか？

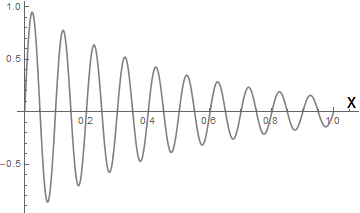
を表す必要がある。まとめて図にすると以下の様になる。波が到達した領域では次々と波の山が進行していくのを見ることになる。尚、前述のド・ブロイ波の議論では時間軸方向での振幅の変化を想定する必要はなさそうだ。

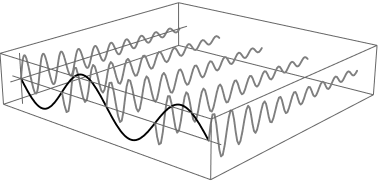
この様に波動方程式は空間の変数と時間の変数が含まれることになる。上記の波動を数式で表すと以下の式の様に、Aが時刻=0、空間＝０における振幅の初期値。e^-bx は空間ｘ方向での波（グレー）の指数的な増減を表し、bはその係数となる。続く e^iｃx はｘ方向におけるグレー波の波数（=2π/λ）であり空間方向での振動を表す。

\[\small \Psi(x,t)=A e^{-b x} e^{i c x} e^{-i \omega t}\\\small \]

最後の e^-iωt が時間軸上での振動を表す。これを、x 軸上と t 軸上に分けて整理すると

\[\small =A e^{i(k x-\omega t)},\quad k=c+b i \]

上記プロット時の各パラメータは A = 0.1; ω = 4π ; v = 0.1; k = 2 π/v + 2 i である。

身近な具体例を挙げると、携帯電話では主に周波数fが数GHzの電波を使う。仮に周波数1G[Hz]の電波の場合、1秒間に10⁹回振動するのでω=2πν=2πx10⁹となる。一方電波は光と同じく1秒で3×10⁸[m]進むので波長:λ=3×10⁸/ν=3×10⁸/10⁹=0.3、つまり30[cm]ということになる。つうまりみんなが携帯電話を使うと10㎝単位の波長を持った電波が、空間のそこらじゅうを飛び交っていると想像すると良い。

ちなみに波動はsin, cos で表記する方が最初はとっつき安いかもしれないが、回転を表す複素指数表現の方が圧倒的に便利だ。あまりなじみが無い方は『信号処理の基礎数学１』やその章で離散フーリエ変換の節を参照願いたい。

時間に依存しないシュレディンガー方程式

電子の波動関数を同じ様に ψ(x,t) の形で表せるとし、波動関数をｘで偏微分する。

\[\small \frac{\partial}{\partial x}\Psi=\frac{\partial}{\partial x}A e^{i(k x-\omega t)}\\\small =ik\Psi \]

一方アインシュタインの見つけた運動量の定義 Eq1.2-3 の \(\small p=\hbar k \) を使って整理すると \[\small \frac{\hbar}{ i}\frac{\partial}{\partial x}\Psi=p\Psi \small \tt \tag{Eq2.2-1} \]

これにより、左辺に掛けた \(\small \left[\frac{\hbar}{ i}\frac{\partial}{\partial x}\right]\) は『波動関数に作用して運動量と波動関数の積を作り出す』と解釈できる。

この\(\small \left[\frac{\hbar}{ i}\frac{\partial}{\partial x}\right]\) を運動量演算子と呼ぶ。

Eq2.2-1をさらにｘで偏微分する。

\[\small \frac{\hbar}{ i}\frac{\partial^2}{\partial x^2}\Psi=i \hbar k^2\Psi\\\small \downarrow\\\small \frac{\partial^2}{\partial x^2}\Psi=-k^2\Psi\\\small \]

ニュートン力学での運動エネルギーを量子論的運動量の定義で拡張し、k²を得る。

\[\small T=\frac{1}{2}m v^2=\frac{1}{2m}p^2=\frac{1}{2m}\hbar^2 k^2\\\small \downarrow\\\small k^2=\frac{2Tm}{\hbar^2} \]

これを一つ前の式に代入るすと

\[\small \ \frac{\partial^2}{\partial x^2}\Psi=-\frac{2Tm}{\hbar^2}\Psi\\\small \]

右辺を運動エネルギーTにのみになるように整理すると

\[\small \ -\frac{\hbar^2}{2ｍ}\frac{\partial^2}{\partial x^2}\Psi=T\Psi\\\small \]

つまり \(\small \ \left[-\frac{\hbar^2}{2ｍ}\frac{\partial^2}{\partial x^2}\right] \) は運動エネルギーを求める演算子といえる。

ニュートン力学で全エネルギーEは運動エネルギーTとポテンシャルエネルギーVの合計となる。これを波動方程式で書くと

\[\small \ -\frac{\hbar^2}{2ｍ}\frac{\partial^2}{\partial x^2}\Psi+V\Psi=(V+T)\Psi\\\small \downarrow\\\small -\frac{\hbar^2}{2ｍ}\frac{\partial^2}{\partial x^2}\Psi+V\Psi=E\Psi \]

空間xによる偏微分方程式となるので波動関数の時間に関する指数関数部は任意の係数 C 同じだ。CAまとめて未定の係数Aと考えて、空間の波動を記述する関数φを以下の様に独立させることができる。

\[\small \Psi=A e^{i k x} e^{i\omega t}=C A e^{i k x}\\\small \downarrow\\\small \phi(x)=A e^{i k x} \]

この部分的な波動関数を使うと以下の様に空間方向に広がった波を記述する方程式ができる。

\[\small \ \left(-\frac{\hbar^2}{2ｍ}\frac{\partial^2}{\partial x^2}+V\right)\phi=E\phi \tt \tag{Eq2.2-2} \]

これをシュレディンガーの『時間に依存しない方程式』と呼ぶ。適用範囲は時間で変化しない定在波の様な限られたものになる。尚、左辺のカッコの中の演算子はハミルトニアン（H)と呼ばれている。

時間に依存するシュレディンガー方程式

次に時間に依存する方を求めてみよう。波動関数を t で偏微分する。

\[\small \frac{\partial}{\partial t}\Psi=\frac{\partial}{\partial t}A e^{i(k x-\omega t)} =-i\omega\Psi \]

両辺に\(\small i\hbar\)を掛け、 Eq1.2-4より \[\small i\hbar\frac{\partial}{\partial t}\Psi=E\Psi \tt \tag{Eq2.2-3} \]

これを時間に依存するシュレディンガー方程式と言う。

3 シュレディンガー方程式の応用

時間に依存しない方程式Eq2.2-2を使って具体的に、ある条件下での電子の波動関数を求めてみよう。解析的に解く場合と数値計算で解く場合の例を解説する。

波動関数の複素共役との積 ψ^* ψは量子の存在確率を与えていると解釈されている。具体的には以下のように全区間を積分すると存在確率＝1になるように規格化して扱うことになる。

\[\small \int_{-\infty}^{+\infty}\psi(x)^*\psi(x)dx=1 \]

規格化前の波形を\(\small\hat{\psi}(x)\)とすると、それの全体の波の形さえ記述できれば、たとえ振幅が未定でも以下の様に波動関数を特定できる。

\[\small \psi(x)=\hat{\psi}(x)/\sqrt{\int_{-\infty}^{+\infty}\hat{\psi^*}(x)\hat{\psi}(x)dx} \]

電子が正の電荷の穴（井戸）の中に落ち込んで出てこれなくなったとしよう。これは正の電荷を持つ原子核に捕捉されている状況に似ているかもしれない。井戸は非常に深いので、計算上、両脇の壁を乗り越える（壁の中にしみ込む）確率を無視できるものとする。ニュートン力学では井戸の中に落ちたボールの運動エネルギーが障壁のポテンシャルエネルギーより小さければ井戸の外に見つかる確率は０だ。ところが量子力学では不確定性によりエネルギー差が小さいと井戸の外でも観測されうる。つまり波動関数が井戸の壁にしみ込んだ形になる。

3.1 無限のポテンシャル井戸の中のに束縛された電子

簡単のため1次元でx軸上に広がる波動関数を求める。井戸の幅をL としとポテンシャルエネルギーを

\[\small V(x)=\begin{cases} \infty \quad x < 0 \\\small 0 \quad 0\leq x \geq L \\\small \infty \quad x>L \end{cases} \]

としよう。尚ここでエネルギーの基準点０をどこにとってもよい。つまり、井戸の外を０とし、井戸の底を ‐∞ としてもよい。波動関数は V-E で定義されており、Eは電子のポテンシャルエネルギーを含む全エネルギーであるので、ポテンシャルエネルギーの絶対値には依存しない。

ド・ブロイ波の考察での通り、電子が原子核の周囲に閉じ込められている場合は波長の整数倍となった。しかし、井戸の壁の間の場合は反射による折り返しのため1/2波長の整数倍の定在波となって存在することになる。以下のは3/2波長の例だ。

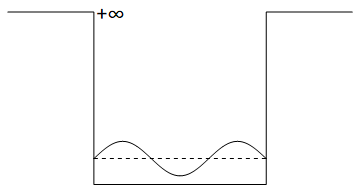
尚、この図で井戸の中の波動関数の高さは見やすいように適当に引いたもので具体的な意味は無い。電子のエネルギ―：Eおよび φの形状はこの後計算により求める。

解析的解

定在波であるため、時間的変動は無いものとして、時間に依存しないシュレディンガー方程式（Eq2.2-2）が使える。

さらに条件により波動関数の壁へのしみ込みは起きない。従って壁の中で想定される波動関数の減衰は考慮不要で、減衰を表すｂは０となる。

\[\small \phi =A e^{i c x}\\\small \]

ｎ番目の定在波となる波動関数の波長λ_nとすると、井戸の幅 L との関係は

\[\small \frac{n}{2}\lambda_n=L \]

波動関数の両端での振幅は０とならなければいけない。従って上記の様に x=0 と x=L で振幅ゼロとなる必要がある。従って

\[\small \phi =A e^{i c x}\\\small \downarrow\\\small \phi=A \space sin\left(\frac{n \pi x}{L}\right) \]

波動関数の共益をφ*とすると、φ*φは電子が存在する確率と解釈されており、 φ*φのx における全区間積分は１となる必要がある。φはこの場合実数のSin関数なので

\[\small A^2 \space \int_{0}^{L} sin^2\left(\frac{n \pi x}{L}\right)dx=1 \]

となり、これををAに関して解けば良い。結果は自然数 n に関係なく

\[\small A=\sqrt{\frac{2}{L}} \]

となるので、波動関数は以下の式で表される。

\[\small \phi=\sqrt{\frac{2}{L}} \space sin\left(\frac{n \pi x}{L}\right) \tt \tag{Eq3.1-1} \]

これを以下のEq2.2-2に代入する。ポテンシャルエネルギーVは条件により、０とする。

\[\small \ \left(-\frac{\hbar^2}{2ｍ}\frac{\partial^2}{\partial x^2}+V\right)\phi=E\phi \]

これにより、以下の等式を得る。

\[\small \ -\frac{\hbar^2}{2ｍ}\frac{\partial^2}{\partial x^2}\sqrt{\frac{2}{L}} \space sin\left(\frac{n \pi x}{L}\right)=E\sqrt{\frac{2}{L}} \space sin\left(\frac{n \pi x}{L}\right) \]

左辺の２階微分を作用させて

\[\small \ \frac{\hbar^2}{2ｍ}\left(\frac{n \pi }{L}\right)^2\sqrt{\frac{2}{L}} \space sin\left(\frac{n \pi x}{L}\right)=E\sqrt{\frac{2}{L}} \space sin\left(\frac{n \pi x}{L}\right) \]

を得る。左右を比較し以下のエネルギーEの等式を得る。

\[\small \ E_n=\left(\frac{\hbar^2 }{2ｍ }\frac{ \pi^2}{L^2} \right)n^2 \tt \tag{Eq3.1-2} \]

これが幅 L の井戸に拘束された1/2λ定在波数ｎの電子のエネルギーを示す関数だ。

実際に波動関数と一緒にプロットしてみよう。電子の様な微小量を扱うので、量子力学の慣例に従いエネルギー単位 [J] を [eV] に変えておこう。1[eV]=1.6022×10^-19[J]だ。従って、

\[\small \ \frac{\hbar^2 }{2ｍ }=6.1034\times 10^{-39}[J\cdot m^2] \\\small =3.8094\times 10^{-20}[eV\cdot m^2] \]

以下、数値に関して有効桁数は考慮していないので参考まで。例としてLが10nm幅の場合のエネルギー Enと振幅Aは

\[\small \ E_n=\left(\frac{\hbar^2 }{2ｍ }\frac{ \pi^2}{L^2} \right)n^2=3.7597\times n^2 [meV]\\\small A=\sqrt{\frac{2}{L}}=0.4472\quad\quad\quad\quad\quad\quad\quad \]

となり、Eq3.1-1, Eq3.1-2 を重ねてプロットすると以下の通りとなる。

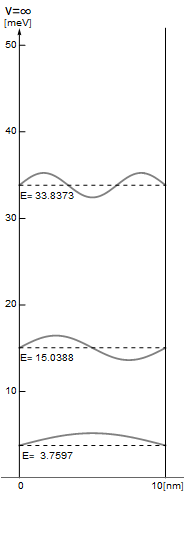
図3.1-1

下からエネルギー準位：n=1, 2, 3 の電子の運動エネルギーE_nと、その波動関数となる。

数式の通りで、今一つ実感がわかない。そこで数値計算によりこの波動関数を再現させてみよう。

数値処理的解

以下シューティング法という差分方程式を使った解法を説明する。

理屈からいうと波は隣から隣に伝わるものであり、ある場所からその少し離れた場所との間に決まり事がある。以下の時間に依存しない方程式(Eq2.2-2)の、波動に関するエキスを抜き出してみよう。

\[\small \ \left(-\frac{\hbar^2}{2ｍ}\frac{\partial^2}{\partial x^2}+V\right)\phi=E\phi \]

左辺カッコの中はエルギー演算子（ハミルトニアン）だが、V=0と置き、係数部を無視して１とすると

\[\small \ -\frac{\partial^2}{\partial x^2}\phi=E\phi \]

この式でｘの方向に（一定速度で）波形をなぞって行く。波形の一階微分を”速度”、二階微分を”加速度”と読み替えると波形の変化をイメージしやすい。例えばこの式は『φの波が高くなると押し下げ、低くなると押し上げる様に加速度が働くと』言っている。さらに『Eが大きいと加速度が大きくなるり、その結果動きが激しくなり、振動数が大きくなる』とも言っている。これは、ニュートン力学での単振動と同じ形をしている。

左辺の２階微分は近接するx軸上の連続で近接する3点を x₁, x₂, x₃ とすると、以下の様に傾きの変化を示す α が０では無いという事を表している。

\[\small \{\phi(x_3)-\phi(x_2)\}=\{\phi(x_2)-\phi(x_1)\}+\alpha \]

そもそも、もしα=0なら3点は直線上に並び、2階微分の項は不要だ。

これらの3点を一般化して表すと

\[\small \{\phi(x_{n+1}-\phi(x_n)\}=\{\phi(x_n)-\phi(x_{n-1})\}+\alpha(x_n) \]

以降、差分法により離散的に処理するので、

\[\small \{\phi[n+1]-\phi[n]\}=\{\phi[n]-\phi[n-1]\}+\alpha[n] \]

と”[“を使って記述しよう。

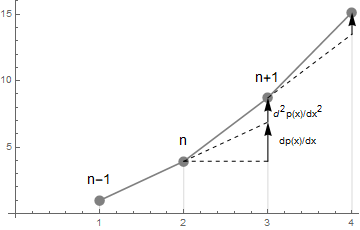
図3.1-2

左辺を一つ先の n+1 となるように変形すると

\[\small \phi[n+1]=2\phi[n]-\phi[n-1]+\alpha[n] \]

ここで波動関数と比較し α＝－Eφ と置けば同じ形になる。

\[\small \phi[n+1]=2\phi[n]-\phi[n-1]-E \phi[n] \]

この様に一つ先[n+1]の値を計算するためには、現在地点[n]の値と一つ前[n-1]の値の二つが必要となる。加速度として働く3番目の項は現在地点[ｎ]の波の高/低にEを掛けたものだ。そこで細かいことを気にせずE=0.1にして、このままプロットしてみよう。グラフの左端にて初期値としてφ[0]=0, φ[1]=1と2点分を設定し、φ[1]を起点として右に向かって19回計算する。

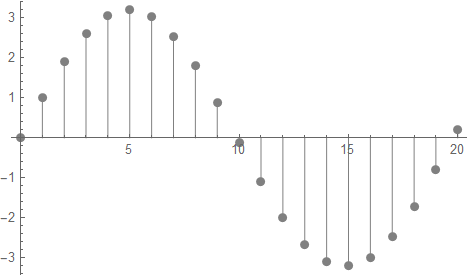
この様に差分方程式から想像しにくいことだが、波動が描かれた。E=0.4にしてみる。つまりエネルギーを2²倍にすると以下の様に振動数は2倍、波長:λ は半分なる。

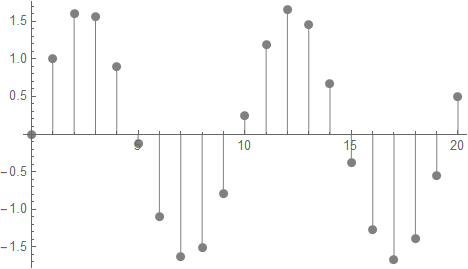
ところで初期値（φ[0]=0, φ[1]=1と2点分の設定）の意味は質点の単振動で言うと、ポンと質点をたたいて[0→1]の勢い（初期速度:v=1）をつけることに相当するイメージだ。勢いを[0→2]とする（初期速度:v=2）と振幅:Aは2倍になるが、振動数はあくまでEで決まる。つまりEはばねの硬さ（と質点の重さ）に相当するとイメージすればよい。

いずれにせよ、この様に差分方程式を構成すると以下のとおり想定した波動関数が再現できることが分かる。

\[\small \ \phi =A e^{i c x} \]

次のステップとして演算精度を上げること考えよう。上記の例は初期点と併せて20点で計算を行った。この数をN_aとし、N_a＝100に増やすと、同じ波形が引き続き4回分続くだけで波形の粗さに変わりは無い。相似形の波形でありながら各点の間隔を詰めて、精度の高い計算結果を得たい。そのためには１階微分の項と２階微分の項をいじる必要がある。

仮に波形の幅: L=1 とすると、２点間の幅: dxは20回の計算では dx=L/20=0.05だ。100回にするとdx=L/100=0.01となる。しかし微分の定義で分母のdxが小さくなると傾きが大きくなってしまう。その結果、微分項に掛かる係数が大きく見えてしまうので、それを補正する必要がある。つまり１階微分の項はΔxを、２階微分の項はΔx²を乗じる必要がある。従って求める差分方程式は以下の通りだ。

\[\small \phi[n+1]=2\phi[n]-\phi[n-1]-E \phi[n] \Delta x^2,\\\small \phi[0]=0,\space \phi[1]=1 \Delta x \]

２階微分の項に対応するEにΔx²、１階微分に対応する初期速度(=φ[1]-φ[0])に関する設定で φ[1]にΔxを設定している。この式を実行すると、以下の様に相似形で滑らかな波形が得られる。

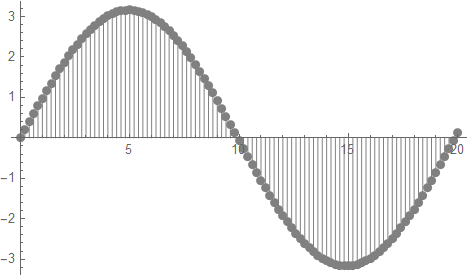
尚、Δxとの関係の参考として、上記の差分方程式は以下と等価だ。

\[\small \begin{cases} \phi'(x)=\phi'(x-\Delta x)-E \phi(x-\Delta x)\Delta x\\\small \phi(x+\Delta x)=\phi(x)+\phi'(x)\Delta x \end{cases} \]

上記の図で振幅は3.14になっているが、規格化前なのでこの値自身に物理的な意味はない。しかしα=0.1と適当に仮置きしたため、右端L=20 で波の節になっていない。1波長での節になるように、αを正確に計算してみよう。いま扱っている差分方程式は、以下の様に微分方程式の近似であることが理解できた。

\[\small \phi[n+1]=2\phi[n]-\phi[n-1]-E \phi[n]\\ \updownarrow\\\small \phi(x)”=-E \phi(x) \]

従って、詳細はEq3.2-1を参考にしてほしいが、この等価な微分方程式を解くと、

\[\small \phi(x)=A\space \sin\left(\sqrt{E}\space x \right) \]

これより、右端で1波長の節にする場合は、以下をEに関して解けば良い。

\[\small \sqrt{E}\space L =2 \pi \]

計算すると仮置きしたE=0.1に代えて、E=0.098696置けばよいことが分かる。

プロットすると以下のグラフの通り、右端L=20できれいに1波長での節となる。

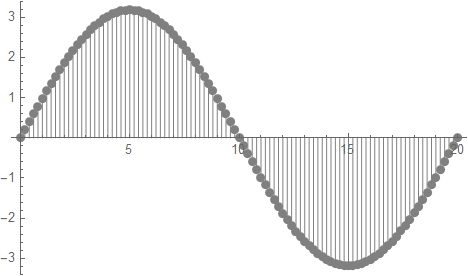
波動差分関数を規格化してみよう。解析的には∫₀^L (φ*φ) dx =1なので、これを参考に

\[\small \frac{L}{N_a}\sum_{n=1}^{N_a}\phi[n]^*\cdot\phi[n]=1 \]

となるように様に振幅を補正したい。従って規格化される前の波動差分関数をハットをつけて表すと、規格化された関数は以下の通りとなる。

\[\small \phi[n]=\hat{\phi}[n]/\sqrt{\frac{L}{N_a}\sum_{n=1}^{N_a}\hat{\phi}[n]^*\cdot\hat{\phi}}[n] \]

プロット時に解析値と高さがそろって便利だ。

これより後は波動関数は規格化されている前提で話を進める。

以上がシューティング法ので利用する差分方程式が、ざっくりとどんなものかの説明となる。

それでは、具体的に係数を考慮して試してみよう。以下Eq2.2-2の波動方程式

\[\small \ \frac{\partial^2}{\partial x^2}\phi=(V-E)\frac{2ｍ}{\hbar^2}\phi \]

と比較して波動差分方程式の係数を組み入れる。

\[\small \phi[n+1]=2\phi[n]-\phi[n-1]+(V[n]-E )\frac{2ｍ }{\hbar^2 }\phi[n] \Delta x^2,\\\small \phi[1]=0,\space \phi[2]=1 \Delta x \]

プロット時に規格化を考慮しているので初期値はこのままとしよう。

以下、解析解での設定値をそのまま使用する。

\[\small 井戸幅:L=10[nm],\quad \frac{\hbar^2 }{2ｍ }=3.8094\times 10^{-20}[eV\cdot m^2] \]

下記の通り、すでに解析的に E_n は求まっているので見当をつけて探る必要はない。正しければ解析解とぴったりと重なるはずであり、シューティング法による検証となる。

\[\small E_n=3.7597\times n^2 \]

以上が差分方程式に新たな加えられた項目だ。まずはn=２を20分割して試してみよう。

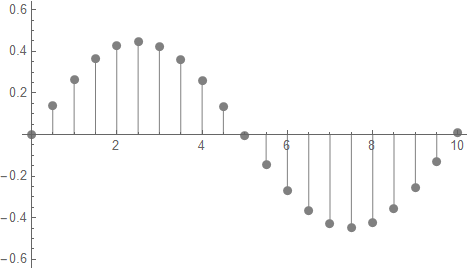
規格化されているので振幅は解析値と同様 √2 となっており、ざっと見で１波長の定在波となっているようだ。

10,000分割し精度を上げて既出の解析解のプロットに重ねてみよう。

以下赤い破線がシューティング法による計算結果だ。解析解によるグレーの結果と正確に一致している。

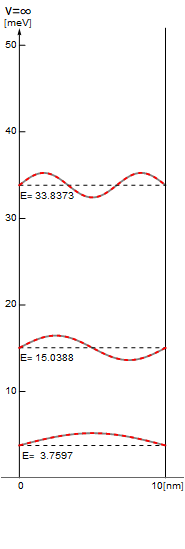
図3.1-3

このシューティング法を使うと手軽に少し複雑な条件でも波動関数の解を得ることができる。試しに有限なポテンシャル井戸を解いてみよう。

3.2 有限のポテンシャル井戸の中のに束縛された電子

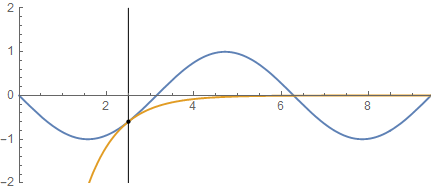
左半分にV=50[meV]で障壁をつくり右半分は0[meV]とし、先ほどの20分割したグラフがどのように変わるかを見てみる。以下の通り、障壁内には指数関数的に減衰しながら侵入している。そして右半分ではSin波が欠けてしまい右端は０となっていない。つまりこのエネルギーのままでは定在波として存在不能となっている。

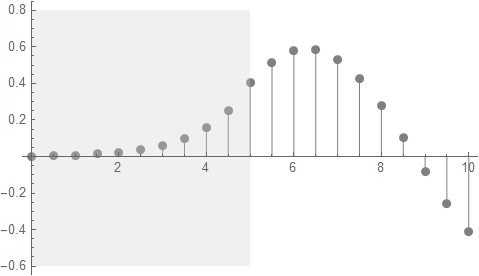
図3.1-4

ここで以下の式でV[n]とEの関係を確認しておこう。

\[\small \phi[n+1]=2\phi[n]-\phi[n-1]+(V[n]-E)\frac{2ｍ }{\hbar^2 }\phi[n] \Delta x^2 \]

左半分の区間はV[n]-E>0となり正のフィードバックが掛かって、右に進むとどんどん大きくなっていく。つまり発散がおきている。逆に言うと障壁の中に向かって指数関数的に小さくなっていく理由である。右半分はV[n]=0であるので、V[n]-E<0となりフィードバックが負となる。つまりいわゆる発振が起きる。これは井戸の中ではV[n]=0なのでV[n]-E<0により、発振してSin波の形となる理由だ。ただ見ての通り右にうまく着地させるのが難しそうだ。三角関数が減衰していく位相で左側と同じ高さにそろえて右の障壁に飛び込み、すっと着地させなければならない。

以上のことを念頭にエネルギーを振って定在波井戸の中での波動関数の形と、適合する電子の運動エネルギーを調べてみよう。左右5[nm]で50[meV]の障壁を設定し電子の運動エネルギーをEを振りながら右端が左端と同様に振幅０に収斂する数値を探り出す。小数点２位の数値の変化でも右端があばれる。探り出した結果は以下の図3.1-5a、-5b、-5cとなる。

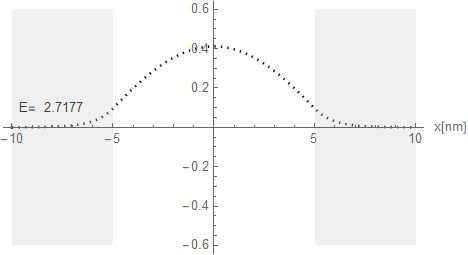
図3.1-5a

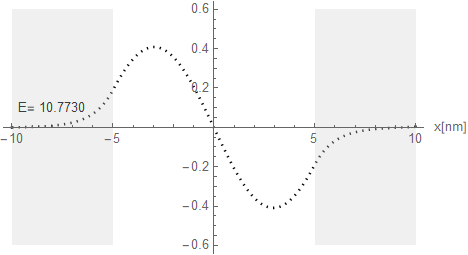
図3.1-5b

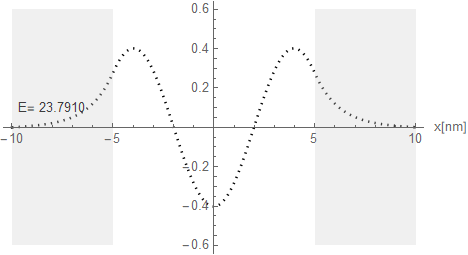
図3.1-5c

エネルギー準位ごとの障壁の中へのしみ込み具合が良くわかる。このしみ込みがトンネル効果と呼ばれるものだ。上記の波形を重ねて比較してみよう。

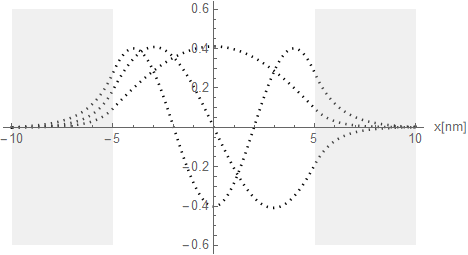
図3.1-5d

壁へのしみ込みが多い波形程、ほんの少しだが井戸の中での振幅が小さくなっていることが分かる。尚、運動エネルギーのあたりを付けるのに使った数値は参考文献１を参照させていただいた。

次に、これを解析的に解いてみよう。シューティング法で理解できた波動関数の形状の前提とし

１）障壁内では指数関数、井戸内では三角関数

２）両端は0となる。

３）障壁と井戸の境界で滑らかに繋がる

上記1）、２）より波動関数の左右（障壁内）は以下の様な指数関数となる。

図3.1-6a

図3.1-6b

そして中央部、つまり井戸の中は以下の様な三角関数波が想定される。以下は図3.1-5dに4番目の準位 E=40.645[meV] を加えたものだ。波形のパターンを確認するための追加したのだが明らかに指数関数部が変だ。障壁の幅が5[nm]では足りないようだ。解析的な解と比較ではっきりすることが出来るだろう。

それはさておき、図上で中央に意識して波形を眺めてみよう。エネルギー準位に応じて赤と緑のCos波(対称)の場合と、オレンジと青のSin波(反対称)の場合に分類できる。

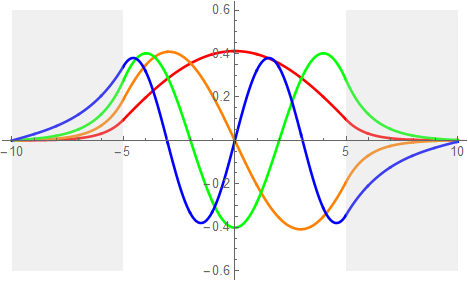
図3.1-6c

赤い波形は1/2波長の基底エネルギ―に対応し、エネルギー準位が上がると波数が増えながら、

\[\small +Cos(k_w x)\quad\rightarrow \quad-Sin(k_w x)\\\small \uparrow\quad\quad\quad\quad\quad\quad\downarrow\\\small -Cos(k_w x)\quad\leftarrow \quad+Sin(k_w x)\\\small \]

を繰り返していくことが想定される。尚、図3.1-3は左右の障壁の高さが無限大の場合の図で、両端で波高が０の”節”となっている。しかし今回考察する障壁が有限の高さ場合は図3.1-6cとの様に左右の壁に節に近づく前に途切れて、指数関数につながることになる。後ほど詳しく説明する。

以上３種類の関数からなる波動関数の形状を理解するために、以下の単純化された波動の差分関数を基に考察してみよう。

\[\small \{\phi[n+1]-\phi[n]\}=\{\phi[n]-\phi[n-1]\}+\alpha\phi[n] \]

尚、以下は前出の図3.1-4であり、もう一度その解説を見直してほしい。

参照：図3.1-4

おさらいとなるが、加速度の様に働くα=V[n]-Eは井戸の外では α>0 だ。従って左側（実際は左無限遠）は条件1)に従い０からはじまり指数的に増加する。井戸の中に到達するとα<0となり、シューティング法での繰り返し計算において、負のフィードバックが働く。これは発振を意味し、これにより三角関数波を描くことになる。

右側の井戸の外に到達すると再び α>0 となる。今度は0に収束させなければならないので、三角関数の振幅が減少する位相で井戸の端に到達させ、うまく a>0 を利用して指数関数的にブレーキをかけ、右端（実際は右無限遠）でピッタリと”0″に止める必要がある。逆に言うと、図3.1-4で波形が右端の手前でx軸と交差した点から対称な位置に右側の壁を置くと、波動関数は定在することができる。

条件３）はSin波と両端の指数関数部とのつながり方の話だ。以下様に井戸の壁でSin波と指数関数は同じ傾きになる必要がある。

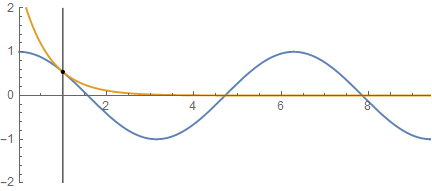
対称形の波形

加速度の様に働くα=(V[n]-E) は一階微分（差分）の方には影響しない。従って（V[n]-E)が井戸の壁の前後で『かくん』と立ち上がるステップ関数になったからと言っても、波動関数の方は折れ曲がらず滑らかにつながらなければならない。

反対称形の波形

上記二つの図に表されたの三角関数と指数関数は以下のよく見かける微分方程式の解となっている。

\[\small \frac{\partial^2}{\partial x^2}\phi(x)= \pm k^2\phi(x),\\\small \tt \tag{Eq3.2-1} \]

[-k² の場合]

\[\small \phi(x)=C_1 \space cos(k\space x)+C_2 \space sin(k\space x) \]

尚、C₁=1, C₂=0 と置くと対称形の波形、C₁=0, C₂=1 と置くと反対称形の波形を表すことができる。

[+k²の場合]

\[\small \phi(x)=C_1 \space e^{k\space x}+C_2 \space e^{-k\space x} \]

これも同様にC₁=1, C₂=0 と置くと井戸の左側の指数的に発散する波形、C₁=0, C₂=1 と置くと右端の指数的に減衰する波形を表すことができる。

シュレディンガー方程式もこのEq3.1-2の式は同じ形をしており、以下の様に少し変形してみよう。

\[\small \ \left(-\frac{\hbar^2}{2ｍ}\frac{\partial^2}{\partial x^2}+V\right)\phi=E\phi\\ \downarrow\\\small \frac{\partial^2}{\partial x^2}\phi(x)=\frac{2ｍ}{\hbar^2}(V-E)\phi(x) \tt \tag{Eq2.2-2′} \]

井戸の中ではE>Vであり、三角関数の解を期待するので、以下の様に負符号をつけた式を適用しよう。

\[\small \frac{\partial^2}{\partial x^2}\phi(x)= -k^2\phi(x),\\\small k^2=2m(E-V)/\hbar^2 \tt \tag{Eq3.2-2} \]

この等の解を使って表すと

\[\small \phi_w(x)=A \space cos(k_w\space x)+B \space sin(k_w\space x),\\\small k=\sqrt{2m(E-V)}/\hbar \tt \tag{Eq3.2-3} \]

Cosは対称な波形の解に、Sinは反対称な波形の解に現れる。

井戸の外ではV>Eであり、指数関数の解を期待するので係数の符号を正とした式を適用する。結果として井戸の左側（L)と右側（R)で以下の解を得る。

\[\small \begin{cases} L: \quad C\space e^{+k_e x}\\ \small R: \quad D\space e^{-k_e x} \end{cases},\\\small k_e=\sqrt{2m(V-E)}/\hbar \tt \tag{Eq3.2-4} \]

解を求める方法として波形の考察から入ってみよう。

赤い波形がEq3.2-3のCosで表された井戸の中の波動関数（右半分）の例だ。井戸の右端の位置:L=0.5を過ぎると青のEq3.2-4で表される指数関数の解となる。

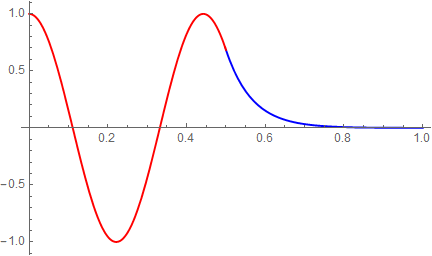
この二つの波形は、その形を見れば以下の形の式で表されていることが、方程式を解くまでも無く理解できると思う。

\[\small \begin{cases} x<L & \phi_t(x)\equiv cos(k_w x) \\ \small x\geq L & \phi_e(x)=\color{green}{\phi_t(L)} e^{\large \color{red}{\frac{\phi_t(L)’}{\phi_t(L) }} \small (x-L)} \end{cases} \tt \tag{Eq3.2-5} \]

指数関数の係数部、つまり先頭部がφ_t(L)となっており、x=L の位置でCos関数と同じ高さを与えている。さらに指数部の係数を φ_t(L)’/φ_t(L) とすることにより、Cos関数の傾きと一致させている。なぜφ_t(L)で割るか少し補足すると、これは指数関数の特質で、水色の 1Exp(-1 x) の始まる高さを単純に 1→0.4 に下げただけでは、オレンジのグラフの通り、傾きが緩やかになってしまう。従って、さらに指数部の係数を0.4で割ることによって、緑のグラフで示された様に同じ傾きを得ることができる。

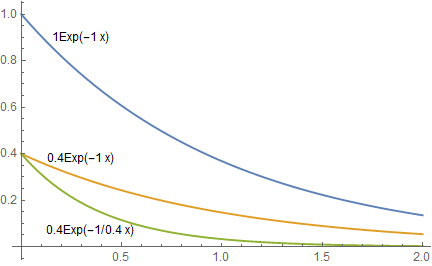
図3.1-7

この事は、波動関数の直観的理解を深める上で重要で、三角関数波が壁に到達した高さが節に近づき、低くなればなるほど、この例の通り指数部の係数が大きくなってくる。係数が大きくなると減衰速度が大きくなることを意味し、そのためにはさらに深い井戸を深くする必要があると言うことになる。そして完全な節で定在するためには無限の深さの井戸が必要になる。これが『3.1 無限のポテンシャル井戸の中のに束縛された電子』の背景だ。

以上の様にEq3.2-5により赤い三角関数と青い指数関数を滑らかにつなぐことができた。この赤いCosの k_w を振って波形を変化させると、壁に到達する高さが変わるので、青い指数関数の方もつられて変化する。その結果、EとVがどう変化するかを見てみよう。

Eq3.2-4と比較すると、係数のDとk_wが特定できる。

\[\small D\space e^{-k_e x}\equiv\phi_t(L) e^{\large \frac{\phi_t(L)’}{\phi_t(L) }(x-L)}\\\small \quad\quad\quad\quad\quad=[\phi_t(L) e^{-L\large \frac{\phi_t(L)’}{\phi_t(L) }}]\space e^{\large \frac{\phi_t(L)’}{\phi_t(L) }x} \]

よって

\[\small D=[\phi_t(L) e^{-L\large \frac{\phi_t(L)’}{\phi_t(L) }}],\quad -k_e= \frac{\phi_t(L)’}{\phi_t(L) } \]

ke は元々

\[\small k_e=\sqrt{2m(V-E)}/\hbar \]

であったので、以下の等式が成り立つ。

\[\small \frac{\phi_t(L)’}{\phi_t(L) }=-\sqrt{2m(V-En)}/\hbar \]

これをVについて解くと

\[\small V=\frac{\hbar^2}{2m} \left(\frac{\phi_t(L)’}{\phi_t(L) }\right)^2+En \tt \tag{Eq3.2-6} \]

ここで\(\small \phi(x)=D \space cos(k_w x)\) なのでEq3.2-6に当てはめると \[\small V=\frac{\hbar^2 k_w^2}{2m}tan^2(k_w L)+En \tt \tag{Eq3.2-6a} \]

以上の様に三角関数波と指数関数波を滑らかにつなぐという条件を満足させるための、EとV、およびk_wの関係式が得られた。

Eq3.2-3で井戸の中ではV=0とすれば電子のエネルギーは以下の様に簡単に求まる。

\[\small En=\frac{k_w^2\hbar^2}{2m} \tt \tag{Eq3.2-7} \]

つまりEは k_w をCos関数の振動速度（実際はk_w t ではなくk_w xなのでちょっと違うが…）とイメージすると、振動速度の2乗に比例している。

\(\small \phi(x)=D \space cos(k_w x)\) の例なのでEq3.2-6aにEq3.2-7を代入して \[\small V=\frac{\hbar^2 k_w^2}{2m}[tan^2(k_w L)+1]\\\small =\frac{\hbar^2 k_w^2}{2m}[sec^2(k_w L)]\space\space \tt \tag{Eq3.2-8} \]

を得、これをプロットする。

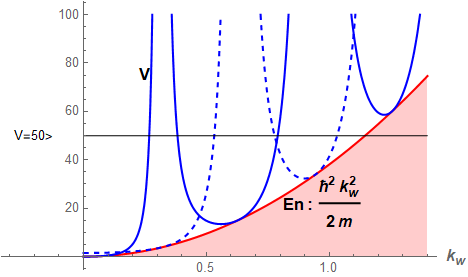
図3.1-8

赤い放物線がEn で青い実線が障壁のポテンシャルエネルギー：Vとなる。

加えて、\(\small \phi_t(x)\equiv C \space sin(k_w x)\) の場合、Eq3.2-8は \[\small V=\frac{\hbar^2 k_w^2}{2m}[cot^2(k_w L)+1]\\\small =\frac{\hbar^2 k_w^2}{2m}[csc^2(k_w L)]\space\space \tt \tag{Eq3.2-9} \]

となり、これにより算出されたVを青い点線で重ねてプロットした。

さてこの図ができたことにより障壁の高さVを指定して、k_wと電子のエネルギー：En が求められるようになった。例として図3.1-5と同じV=50[meV]で計算してみよう。つまり以下の等式を

\[\small 準位[1, \space 3]: \quad 50=\frac{\hbar^2 k_w^2}{2m}[sec^2(k_w L)] \]

\[\small 準位[2, \space 4]: \quad 50=\frac{\hbar^2 k_w^2}{2m}[csc^2(k_w L)] \]

をk_wに関して解けば良い。しかしこの場合、式は二つのk_wの関数の合成関数の形となっており、k_wをVの関数の形に変形できない。そこで図にV= 50 の線を引き、Vの立ち上がりの曲線との交点をおおざっぱに求め、その近傍でニュートン法などにより数値解析的に根を求めることになる。もちろんVが求まればEnはEq3.2-7により簡単に求められる。

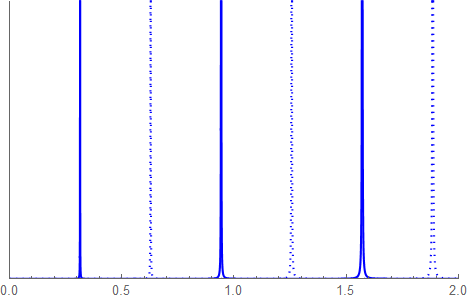
以下の表はMathematicaのFindRoot関数を使った。図3.1-6cの図で水色の第一準位は+Cos波に対応するので、図3.1-8上の青い実線との最初の交点、Kw≈2.5当たりにとを指定すれば良い。

準位（量子数）	k_w	En[meV]	中央部の関数形状
1	0.267099	2.71767	+Cos[k_w x]
2	0.53178	10.7725	-Sin[k_w x]
3	0.790244	23.789	-Cos[k_w x]
4	1.03223	40.5888	+Sin[k_w x]

表3.3-1

2番目はオレンジ色の -Sin波で K_w=0.5 、3番目は緑色の -Cos波で k_w=0.75、4番目はオレンジ色の +Sin波で k_w=1を指定して根を求めた。この結果はシューティング法による図3.1-5a、-5b、-5cと高い精度で一致している。

指数関数の方はEq3.2-4により VとEn から減衰に関する指数部の係数：k_eが求められる。振幅の係数：Dは中央部の三角関数に井戸の端：x=L を代入すれば求まる。

まずは三角関数の振幅係数：A=1と仮置きして以上を計算し三角関数波と指数関数波をつなげてプロットしてみよう。以下は順位１の規格化する前の波形となる。

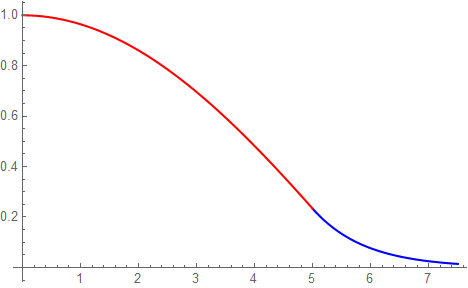
これを以下の様に規格化処理すれば波動関数が求まる。

規格化係数を1/Sとすると、以下の様に\(\small S=\sqrt{(S_t)^2+(S_e)^2}\)を求めれば良い

井戸の中の三角関数波部

\[\small (S_t)^2=2\int_{0}^{L}\phi_t(x)^*\phi_t(x)dx \]

は

\[\small =\begin{cases} \scriptsize \phi_t(x)=cos(k_w x): & \small L+\large\frac{sin(2 k_w L)}{2 k_w} \\ \scriptsize \phi_t(x)=sin(k_w x): & \small L-\large\frac{sin(2 k_w L)}{2 k_w} \end{cases} \]

が解である。

障壁の中の指数関数波部では

\[\small (S_e)^2=2\int_{L}^{\infty}\phi_e(x)^*\phi_e(x)dx =-\frac{\phi_t(L)^2}{2\phi_t'(L)/\phi_t(L)} \]

より、

\[\small =\begin{cases} \scriptsize \phi_t(x)=cos(k_w x): & + cos^2 ( k_w L)cot(k_w L) \\ \scriptsize \phi_t(x)=sin(k_w x): & – sin^2 ( k_w L)tan(k_w L) \end{cases} \]

で求められ、規格化前の関数全体に1/Sを掛ければ良い。

尚、積分の頭に２が掛かっている理由は、右半分だけしか積分していないので、計算結果を2倍して補正するためだ。

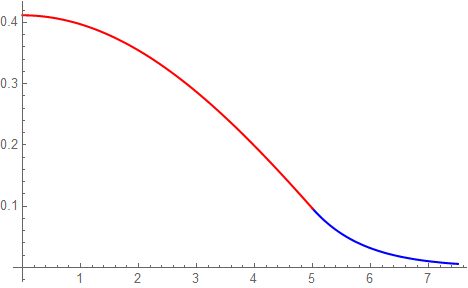
解析的に解いたこれ等のグラフを、シューティング法によるものと重ねて確認してみよう。表3.3-1でエネルギ―準位の1から3までは、Eが精度良く一致していることを確認しているので、以下の三つはきれいに重なっている。

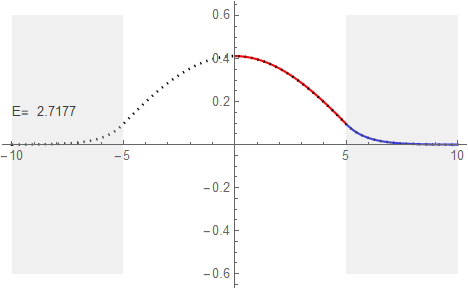
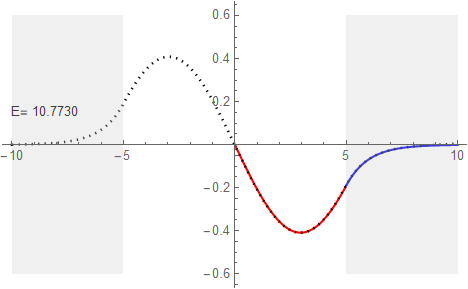
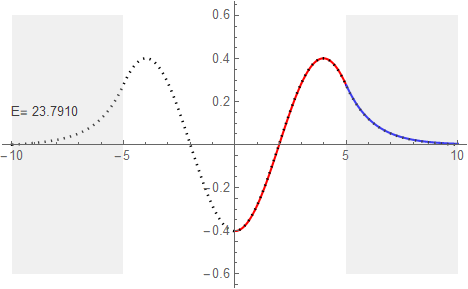
しかし準位４の場合、解析値ではE=40.5888となっておりシューティング法による40.6450に対して差が大きく、グラフも右端でのずれがはっきりと確認できる。

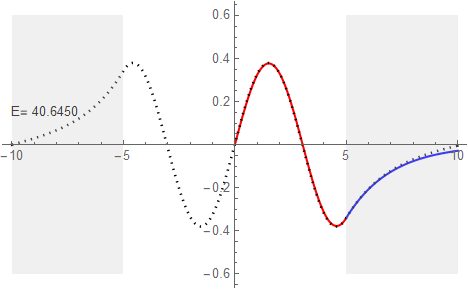
もちろん解析値の方が正確だ。指数関数部の形を見れば分かると思うが、他と比べ障壁へのしみ込みが大きい。従って青い指数関数が右端で0に収束しきれていない。ところがシューティング法での場合は右端で無理やり0に着地させている感じだ。つまり誤差の原因はシューティング法で準備した左右の壁の幅が足りていなかったためだと理解できる。

井戸をどんどん深くしていくと図3.1-8における運動エネルギーVは以下の図の様にの様に、とがっていき、\(\small n \pi\) に収束していく。これが『3.1 無限のポテンシャル井戸の中のに束縛された電子』に相当する。

以上で量子の波動関数による表現が何か、量子状態とは何かが実感できたのではと思う。水素原子は陽子の正の電荷によりり電子を束縛しているがポテンシャル井戸の電子と同様にエネルギーの準位が存在する仕組み（量子状態）は同じだ。水素原子の三次元に広がった波動関数を算出するのも興味深いものがあるが、別の機会としよう。

4. 場の量子論への準備

第3章での通り波動関数は以下の様に量子の存在確率を表す。

\[\small \int_{-\infty}^{+\infty}\psi(x)^*\psi(x)dx=1 \]

これにより、運動量ｐを求める場合は以下Eq2.2-1の

\[\small \frac{\hbar}{ i}\frac{\partial}{\partial x}\Psi=p\Psi \]

運動量演算子を左右から挟んで積分すると運動量ｐが求められる。

\[\small \int_{-\infty}^{+\infty}\psi^*\frac{\hbar}{ i}\frac{\partial}{\partial x}\psi dx=p\cdot 1 \]

量子電磁気学で有名なディラックがこれを以下の様に簡略化した。

\[\small \langle \psi \mid \frac{\hbar}{ i}\frac{\partial}{\partial x}\mid \psi\rangle =p \]

左をブラ、右をケット、併せてブラケットだそうだ。

エネルギーを求める場合はEq2.2-2のエネルギ―演算子（ハミルトニアン：H）

\[\small \left(-\frac{\hbar^2}{2ｍ}\frac{\partial^2}{\partial x^2}+V\right)\psi=E\psi \]

を同様にブラとケットで挟んで

\[\small \langle \psi \mid -\frac{\hbar^2}{2ｍ}\frac{\partial^2}{\partial x^2}+V\mid \psi\rangle =E \]

と書く。

続く　＞

参考文献

1 最も分かりやすいシュレディンガー方程式の入門書　竹内淳著　講談社

2 理論物理学入門　都築卓司　総合科学出版

3 物理数学のためのMathematica ロバート・ジンマーマン/フレデリック・オルネス著　ピアソン・エデュケーション

Post Views: 15