本稿は一般相対性理論2 [リーマン幾何学編]から続いての解説となる。曲率テンソルから、いかに重力方程式にたどり着いたかを理解する。引き続き可能なかぎり数式処理 (CAS) を使って視覚化を行い、直観的理解を補助する。
3.1 ビアンキの関係式
前章で説明した曲率テンソルを基に重力場の理論を構築することになる。引き続き関連する数学的な準備を進めておこう。
曲率テンソルの対称性
曲率テンソルにはいろいろな対称性がある。あらためて曲率テンソルの定義を以下の様に書き直しておく。
\[\small
A^h_{\space :j:k}-A^h_{\space :k:j}=R^h_{ijk}A^i\space ,\quad\quad\quad\quad \\\small
R^h_{ijk}=\Gamma^h_{ji,k}-\Gamma^h_{ki,j}
+\Gamma^h_{lk}\Gamma^l_{ji}-\Gamma^h_{lj}\Gamma^l_{ki}
\]
簡単に分かることに( j,k )の入れ替えだ。ベクトルの移動経路を入れ替えると符号が反転する。
\[\small
R^h_{ijk}=-R^h_{ikj}
\tt \tag{Eq3.1-1}
\]
Rを全て共変成分に変えてみよう。
\[\small
g_{hl}R^l_{ijk}=R_{hijk}
\]
以下の二つの対称性が分かる。
\[\small
R_{\underline{hi}jk}=-R_{\underline{ih}jk}\space,\\ \small R_{hi\underline{jk}}=-R_{ih\underline{kj}}
\tt \tag{Eq3.1-2}
\]
次に気が付くのは( h, j, k )の循環入れ替えだ。
クリストッフェルの下付きインデックスには対称性があるので、以下の様に入れ替えた三つを足し合わせるとゼロとなる。
\[\small
R^h_{ijk}=\Gamma^h_{ji,k}-\Gamma^h_{ki,j}
+\Gamma^h_{lk}\Gamma^l_{ji}-\Gamma^h_{lj}\Gamma^l_{ki}\\\small
R^h_{jki}=\Gamma^h_{kj,i}-\Gamma^h_{ij,k}
+\Gamma^h_{li}\Gamma^l_{kj}-\Gamma^h_{lk}\Gamma^l_{ij}\\\small
R^h_{kij}=\Gamma^h_{ik,j}-\Gamma^h_{jk,i}
+\Gamma^h_{lj}\Gamma^l_{ik}-\Gamma^h_{li}\Gamma^l_{jk}\\\small
\]
\[\small
R^h_{ijk}+R^h_{jki}+R^h_{kij}=0
\tt \tag{Eq3.1-3}
\]
その他いくつかの対称性
\[\small
R^{hijk}=R^{jkhi}=R^{kjih}
\tt \tag{Eq3.1-4}
\]
等により、曲率テンソルの独立な成分は20個まで少なくなる。
ビアンキの恒等式
ベクトルの積を微分する場合、次の様に『関数の積の微分』が成り立つ。
\[\small
(A_i B_j)_{,k,l}=(A_{i ,k}B_j+A_i B_{j,k})_{,l}
\]
同様にベクトルの共偏微分も『関数の積の微分』が成り立つ。
\[\small
(A_i B_j)_{:k:l}=(A_{i :k}B_j+A_i B_{j:k})_{:l}
\]
さらに展開する。
\[\small
=A_{i :k:l}B_j+A_{i :k}B_{j:l}+ A_{i :l}B_{j:k}+ A_i B_{j:k:l}
\]
kとlを入れ替えて引く
\[\small
(A_i B_j)_{:k:l}-(A_i B_j)_{:l:k}\\\small
=A_{i :k:l}B_j-A_{i :l:k}B_j+ A_i B_{j:k:l}- A_i B_{j:l:k}\\\small
=(A_{i :k:l}-A_{i :l:k})B_j+ A_i (B_{j:k:l}- B_{j:l:k})\space\space\space
\]
カッコ内を曲率テンソルとベクトルの積にまとめる。
\[\small
=A_h R^h_{ilk}B_j+ A_i B_hR^h_{jkl}\quad\quad\quad\quad\quad\space\space
\]
ABをテンソルTみなすと、上記の式は
\[\small
T_{ij:k:l}-T_{ij:l:k}=T_{h j}R^h_{ilk}+ T_{ih}R^h_{jkl}
\]
を表している。そこでTijの部分にベクトルの共変微分Vi:jを当てはめてみると
\[\small
V_{i:\underline{j:k:l}}-V_{i:\underline{j:l:k}}=V_{h :j}R^h_{ilk}+ V_{i:h}R^h_{jkl}
\tt \tag{Eq3.1-5}
\]
を得る。この式より、左辺でアンダーラインを引いたインデックス( j, k, l ) に関しては任意の入れ替えが可能だと分かる。
そこで左辺を( j, k, l )を巡回的に入れ替えてみよう。1回目は以下の様に( k, l, j ) と入れ替え、曲率とベクトルとの積に変形後、さらに共変微分を展開する。
\[\small
V_{i:\underline{k:l:j}}-V_{i:\underline{l:k:j}}=(V_h R^h_{ikl})_{:j}\\\small
=V_{h:j} R^h_{ikl}+V_h R^h_{ikl:j}
\]
右辺(Eq3.1-4)もインデックスを同様に入れ替え、あらためて等式を結ぶと以下の通り。
\[\small\underline{ \underline{V_{h:j} R^h_{ikl}}}+V_h R^h_{ikl:j}=\underline{ \underline{V_{h :k}R^h_{ijl}}}+ \underline{V_{i:h}R^h_{klj}}\]
ここで、2重にアンダーラインを引いた項は左右同じなので消去できる。さらに右辺でアンダーラインを引いた項は3巡回の足し合わせで Eq3.1-3より0となる。従って残りの項のみを足し合わせれば以下の等式を得る。
\[\small V_h (R^h_{ijk:l}+R^h_{ikl:j}+ R^h_{ilj:k})=0\]
この等式は、Vが任意のベクトルで成り立たなければいけないので
\[\small R^h_{ijk:l}+R^h_{ikl:j}+ R^h_{ilj:k}=0
\tt \tag{Eq3.1-6}
\]
となる。これはビアンキの恒等式と呼ばれ、この後重力方程式を構築する上で重要なものとなる。
3.2 アインシュタインテンソル
ビアンキの恒等式 Eq3.1-6 で以下の様に非対称性の添字を縮約する。
\[\small
R^h_{ijk:h}+R^h_{ikh:j}+ R^h_{ihj:k}=0
\]
さらに計量を掛ける。
\[\small
g^{ij}(R^h_{ijk:h}+R^h_{ikh:j}+ R^h_{ihj:k})=0
\]
計量gは共変微分に対し定数並みに扱えるので各項に分配する。
\[\small
(\underline{g^{ij}R^h_{ijk}})_{:h}+(g^{ij}R^h_{ikh})_{:j}+ (g^{ij}R^h_{ihj})_{:k}=0
\]
上記第1項のカッコ内の添字を一旦下げ、Eq3.1-2の対称性 \(\small R_{hijk}=-R_{ihjk}\) を使って以下の様に変形する。
\[\small
\underline{g^{ij}R^h_{ijk}}=g^{ij}g^{hl}R_{lijk}=-g^{ij}g^{hl}R_{iljk}\\\small
=g^{ij}g^{hl}R_{lijk}=g^{hl}R_{lk}=R^h_{\space k}
\]
これにより恒等式は以下の様になる。尚、第3項は\(\small R_{hijk}=-R_{ihkj}\)を適用してある。
\[\small
(R^h_k)_{:h}+(g^{ij}R^{\underline{h}}_{ik\underline{h}})_{:j}-(g^{ij}R^{\underline{h}}_{ij\underline{h}})_{:k}=0
\]
さらにgの添字も縮約する。
\[\small
(R^h_k)_{:h}+(R^j_{k})_{:j}-(R)_{:k}=0
\]
第1項、2項のダミーインデックスをhに統一し合算すると以下の等式を得る。
\[\small
2R^h_{k:h}-R_{:k}=0
\]
しかし共変微分が第1項、2項ばらばらだ。統一したい。そこで以下の
\[\small
\delta^h_l=\left(\small \begin{array}{c}1&0\\ \small 0&1\end{array}\right)
\]
δklを両項に掛ける。
\[\small
2\delta^k_l R^h_{k:h}-\delta^k_l R_{:k}=0
\\\small\small\small↓\\\small
2 R^h_{l:h}-\delta^k_l R_{:k}=0
\\\small\small\small↓\\\small
2 R^h_{l:h}-\delta^h_l R_{:h}=0
\]
と共変微分用のダミーインデックスが統一できる。共変微分の添字をカッコの外にくくりだし、両辺に1/2を乗ずると恒等式は最終的に
\[\small
\left(R^h_{\space l}-\frac{1}{2}\delta^h_{\space l }R\right)_{:h}=0
\tt \tag{Eq3.2-1}
\]
と書き表すことができる。
リッチテンソル、スカラー曲率
曲率テンソル Rhijk の k=h と置いて縮約する。
\[\small
R_{ij}\equiv R^h_{\space ijh}
\tt \tag{Eq3.2-2}
\]
これをリッチテンソルと呼ぶ。Eq3.1-4に gij を掛けると分かるように、対称成分を持つ。
さらに縮約して
\[\small
R\equiv g^{ij}R_{ij}
\tt \tag{Eq3.2-3}
\]
をスカラー曲率と呼ぶ。
3.3 重力方程式
ニュートンの重力理論
相対性理論によるの重力理論に進む前に、ニュートン力学における重力理論のおさらいをしておこう。
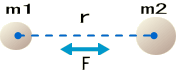
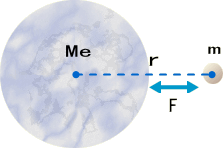
二つの質点m1、m2間に働く力は、万有引力と呼ばれ
\[\small
F=G\frac{m_1 m_2}{r^2},\quad\quad
\\\scriptsize G\space≒\space 6.7\times10^{-11}[kg^2]
\]
となる。 2つの質点間に働く力を定めた、あの有名なニュートンの万有引力の方程式だ。
片方を惑星程度の大きさとする(Me>>m)と、力は惑星の及ぼす重力となり、以下は重力方程式となる。
\[\small
F=G\frac{m \space M_e}{r^2},\quad\quad
\\\scriptsize G\space≒\space 6.7\times10^{-11}[kg^2]
\]
Me>>mであるので、質点に働く加速度αは以下の様に記述できる。
\[\small
\alpha=\frac{F}{m}=-G\frac{ M_e}{r^2}
\]
重力ポテンシャルを以下の様に定義すると、
\[\small
\phi=-\int G\frac{M_e}{r^2}dr= G\frac{M_e}{r}
\]
加速度はポテンシャルの微分となる。
\[\small
\alpha=\frac{d \phi}{dr}
\tt \tag{Eq3.3-1}
\]
ポアソンの方程式
以上の方程式は質点が一点に集中しているような単純な状況でしか成り立たない。そこで質量が広がって分布する場合に拡張する必要がある。
『重力場理解のための、イメージトレーニング』
質量からは仮想の重力線注)が湧き出している。
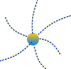 質量が大きいほど、線の数が多い。 質量は重力線を供給する源泉と考える。
質量が大きいほど、線の数が多い。 質量は重力線を供給する源泉と考える。
注)重力線という物理実態は存在しない。教科書には載っていないが重力場を考える上で、電磁気学における電気力線と同じように、思考を助けるための便宜的な力線をイメージしよう。
ある空間点で、単位面積δSあたりの重力線が多いほど、重力は強い。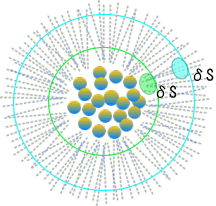
[重力=重力線密度]
質量を囲った緑の球面も青の球面も、突き抜ける重力線の総数は同じ。結果、緑の重力線密度が青より高くなる。
だから、質量源に近い方(緑)が重力は強くなる。半径Rの球の面積は4πr²。 重力線密度は1/(4πr²)に比例。
だから重力は逆二乗の力となる。
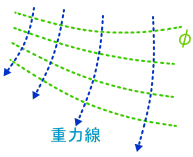 重力は重力ポテンシャルφを創る。重力(加速度)を積分すると重力ポテンシャルとなる。
重力は重力ポテンシャルφを創る。重力(加速度)を積分すると重力ポテンシャルとなる。
ポテンシャルはスカラー。複雑な質量分布でも、距離だけでポテンシャルを計算し、空間軸で微分すると重力加速度のベクトルを求められる。
等ポテンシャル面に垂直に、重力線が走る。等ポテンシャル面の間隔が詰んでいるほど、重力線の密度も高くなる。
以下の様にMの微小質点が空間に分布していたとしよう。
点Pでの重力ポテンシャルは
\[\small
\phi(p)=G\sum^n_{k=1}\frac{ M_k}{r_k}
\]
で与えられる。
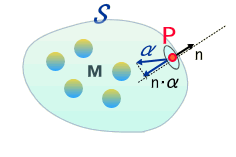
以下の様に任意の曲面Sで囲まれた領域中に、質点が複数存在し、その全質量がMである場合、
その曲面上での重力加速度の法線成分α(つまり面の外に垂直な単位ベクトルnとの内積)を、Sの全曲面にわたって積分すると
\[\small
\iint_S (n\cdot \alpha)dS=-4\pi G M,\quad \alpha=\phi_{,i}
\]
と表される。 これは重力場でも、電荷による電場(電界)でも同じであり、電磁気学ではガウスの定理と呼ばれる基本的な法則だ。
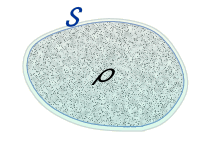
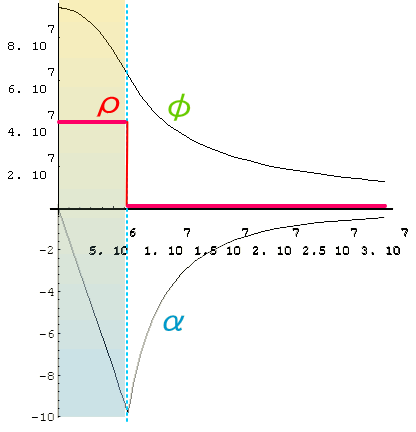
この考えをさらに推し進めて、質量密度ρである領域に適用すると、
\[\small
\phi(p)=G\sum^n_{k=1}\frac{ M_k}{r_k}
\\\space\space \downarrow \\\small
\phi(p)=G\iiint_V\frac{ \rho}{r}dV
\]
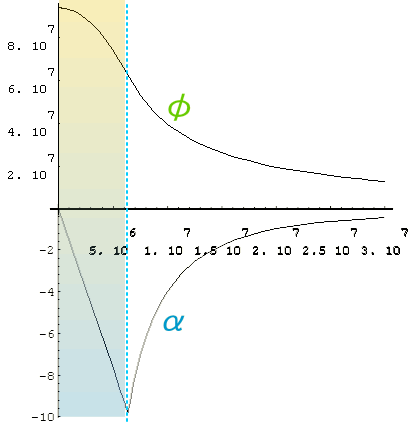
例として、地球のように球形の質量密度分布(一定と仮定)における、重力ポテンシャルφと重力加速度αの分布を見てみよう。
さらにガウスの定理は
\[\small
\iint_S (n\cdot \alpha)dS=-4\pi G \iiint_V\rho\cdot dV,\quad \alpha=\phi_{,i}
\]
と拡張できる。
これよりポテンシャルは
\[\small
\phi_{,,i}=4\pi G \rho
\tt \tag{Eq3.3-2}
\]
ベクトル解析的に言うと、重力ポテンシャルの傾斜:grad φ(=φ,i つまり重力)を取り、さらにその発散: div(div grad φ = φ,,i)を示していることになる。重力の発散とは『重力線の湧き出し口』が増えることを意味し、以下の図の様に質量の分布しない空間(ρ=0)からは重力線が増えない事を意味する。
この地球の例では質量密度が均一に分布していと仮定しているため、重力加速度の大きさ|α|は、地表まで直線的に増える。
地表を過ぎると質量密度はゼロになる。 重力線の湧き出し口が無くなるため、これ以上領域Sを広げてても、領域S上の重力線総数は増ない。 逆に閉領域V内の質量密度とS面上の重力線密度は同時に下がっていく。 その事が|α|の減少に現われていると見ることが出来る。
この式はポアッソンの方程式と呼ばれ、電磁気学等でもよく利用される。
このポアッソンの方程式により重力場を記述すると、万有引力Fが表に出こない。
相対性理論の基本は物理量を4元化し、テンソル方程式により物理法則を記述することにある。そういう意味では単純な引力Fは相対性理論における重力理論の出発点としては適切では無いといえよう。
今まで見てきたように、時空の曲がりと重力場との間には、密接な関係予想る。このポアッソンの方程式の左辺は、φ,,iという4元ベクトルに拡張可能な量を含んでいる。
以降、この方程式を相対性理論化する、つまりテンソル方程式に拡張することを考よう。
アインシュタインの重力理論
Eq3.3-2のポアッソンの方程式をもう一度書くと、以下の様に左辺はポテンシャルの2階微分方で右辺は重力の発生元だ。
\[\small
\phi_{,,i}=4\pi G \rho
\]
4πGは係数なので質量密度ρが重力場を決めていると言える。一方リッチテンソルは計量の2階微分となっている。アインシュタインは計量が重力場のポテンシャルであると考えた。この考えはごく自然だ。相対性理論1 のベクトルの平行移動の章で曲線座標上を直進しようとすると、見かけの加速度 Γ が加えられることを議論した。
このΓ は曲線座標の計量の一階微分となっており α=φ,i を連想させる。当初アインシュタインはΓ を微分した量であるリッチテンソル Rij を φ,,i に代わるポテンシャルの項となるのではとあたりを付け、一度以下の重力方程式を発表した。
\[\small
R^{ij}=kT^{ij}\]
右の T はエネルギー運動量テンソルと呼ばれる量だ。
しかしこの方程式には保存則に問題があり、(空っぽの空間では、つまりTij=0の場合 Rij=0 は成り立つが、)最終的にリッチテンソルを以下の様にアインシュタインテンソルに置き換えて重力方程式を完成させた。
\[\small
G^{ij}=kT^{ij}
\tt \tag{Eq3.3-3}
\]
エネルギー・運動量テンソル
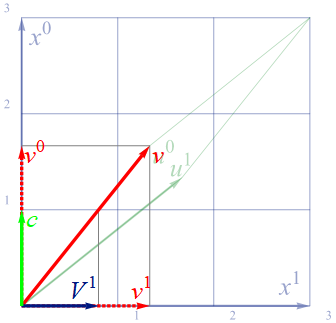
まず右辺の Tij は何かを確認しよう。特殊相対性理論3 [力学編]の議論を通して、我々のよく知るニュートン力学の質量 m0 やエネルギー m0v2/2 は、速度が遅い場合( v ≪ c ) に以下の図の四元運動量ベクトル pi の時間成分に現れてくる力学的量でしかないことが分かっている。
従って右辺はエネルギーおよび運動量を表す何らかの四元量とするのが妥当だと言える。
エネルギーは 特殊相対性理論3 [力学編] Eq3.3-11 の通り
\[\small
E=mc^2=\gamma m_0 c^2=\frac{1}{\sqrt{1-\left(\frac{v}{c}\right)^2}} m_0 c^2
\]
このエネルギー E が、ある系において、体積 W0 の中に分布していたとする。そうするとエネルギー密度は
\[\small
\frac{E}{W_0}
\]
これを別の慣性系から観測すると進行方向に 1/γ だけローレンツ収縮するためニュートン力学における質量密度 ρ とすると、系に依存しない一般的なエネルギー密度は
\[\small
\rho_E=\gamma\frac{E}{W_0}=\gamma\frac{\gamma m_0 c^2}{W_0}\\\small
=\frac{ m_0 }{W_0}\gamma c \gamma c=\rho \gamma c \gamma c
\]
と表すことができる。
図より分かる通り、γcは4元速度 v の時間成分 v0 のことである。従ってエネルギー密度は
\[\small
\rho_E=\rho v^0 v^0
\]
と表すことができる。一方運動量密度の方は
\[\small
\rho_p=\frac{m_0 v^1}{W_0}=\gamma \rho v^1=\frac{1}{c} \rho v^0v^1
\]
となる。
ここで、(ρvivj) を重力元の本質とみなし、エネルギー密度と運動量密度をまとめて、以下の エネルギー・運動量テンソル: T と表す。
\[\small
T^{ij}=\rho v^i v^j \quad\quad\quad\quad\quad\quad\quad\quad\quad\\\small
=\left(\begin{array}{c}
\rho_E & c\rho_p^1 & c\rho_p^2 & c\rho_p^3\\
c\rho_p^1 & \rho_pv^1 v^1 & \rho_pv^1 v^2 & \rho_pv^1 v^3\\
c\rho_p^2 & \rho_pv^2 v^1 & \rho_pv^2 v^2 & \rho_pv^2 v^3\\
c\rho_p^3 & \rho_pv^3 v^1 & \rho_pv^3 v^2 & \rho_pv^3 v^3\\
\end{array}\right)
\]
\(\small
\tt \tag{Eq3.3-4}
\)
この成分中で特にエネルギー密度は T00 、運動量密度は T0j/c であるとする。
慣性系間でのエネルギー運動量の保存則は以下の式で表される。
\[\small
T^{ij}_{\space\space\space,\space j}=0
\]
これを一般座標変換まで拡張すると
\[\small
T^{ij}_{\space\space\space :j}=0
\tt \tag{Eq3.3-5}
\]
となる。
アインシュタインテンソル
次にアインシュタインの重力方程式:\(\small G^{ij}=kT^{ij}\) の左側を掘り下げてみよう。
アインシュタインテンソルは以下の様に定義される。
\[\small
\begin{cases}
G_{ij}\equiv R_{ij}-\frac{\large 1}{\large 2}g_{ij}R\\ \\ \small
G^{ij}\equiv R^{ij}-\frac{\large 1}{\large 2}g^{ij}R
\end{cases}
\]
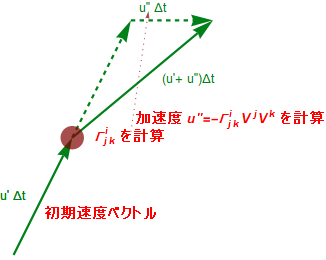
地球の様な弱い重力下のな質点の運動方程式を考える。つまり測地線がどのような形をしているかを探る。いま地表にいて、歪んだ座標系から局所ローレンツ系における慣性運動を眺めているとする。この状況ではすでに述べた通り、曲線座標への変換による以下の見かけの加速度が生じる。
\[\small
\alpha^i=\Gamma^i_{jk}v^jv^k
\tt \tag{Eq3.3-6}
\]
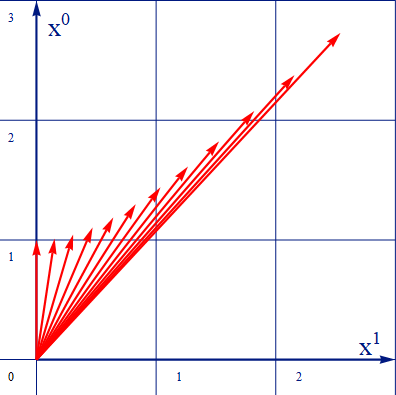
四元速度vはどの様なものだったかおさらいしておく。空間成分はx1のみとすると、ニュートン速度Vをどんどん大きくしていくと以下の図の通り光の速度を表す45度方向に伸びて行く。この図の中で x0=1 の直線と4元速度ベクトルの交点が、ニュートン速度Vに相当する。
質点のニュートン速度Vが十分低速(V≪c)である場合(2番目の速度ベクトルでも5万km/s程度にはなる!)、右から左にベクトルの頭がたどる軌跡(双曲線)を追いかけると分かるように、最後は時間軸X0=c に漸近して上下の変動が無くなる。したがって時間軸方向の変位は無視でき、空間方向X1の成分みを考慮すればよい。これにより四元速度viは
\[\small
v^i\approx[c,V^1]
\]
と表すことができる。ここで空間成分の V1 を重力の方向とし、他は0としして検討を進めよう。
このviをEq3.3-6に適用してみる。二次の微小量を以下の様に無視しすると、
\[\small
\left(\frac{V}{c}\right)^2\approx 0
\]
クリストッフェルの係数で以下の様に、下付き jk 成分に[k:速度ベクトル c]を、[j:時間方向に c だけ移動する]と設定すればよく、その結果 i 成分には加速度が計算される。
\[\small
\alpha^i=\Gamma^i_{00}\space c\space c
\]
地表系 (t,x)から観測する測地線の線素を仮置きで
\[\small
ds^2=(1+2\frac{\phi}{c^2})c^2dt^2-dx^2
\]
とすると
\[\small
\alpha^i=\Gamma^i_{00}\space c\space c=\frac{1}{1-\large \frac{2\phi}{c^2}}\phi_{,i}\approx\phi_{,i}
\]
となり、この線素の定義使うと Γ はうまくニュートンの重力加速度を再現出来ている。
ところで、右辺のエネルギー運動量は保存則
\[\small
T^{ij}_{\space\space\space :j}=0
\]
が成り立つ必要があった。左辺となるアインシュタインテンソルの共変微分はビアンキの恒等式 Eq3.1-6 により
\[\small
\begin{cases}
G_{ij:k} =g_{ik}(R^k_{ j}-\frac{\large 1}{\large 2}\delta^k_{ j} R)_{:k}=0\\ \\ \small
G^{ij}_{\space\space\space:k} =g^{kj}(R^i_{k}-\frac{\large 1}{\large 2}\delta^i_{ k} R)_{:k}=0
\end{cases}
\]
が成り立つ。リッチテンソル、δは対称な成分を持つので上が成り立てば、下も成り立つ。これはリッチテンソル単独では成り立たない。
ここで k を以下の様にとると、ポアッソンの方程式と一致させることができる。
\[\small
G^{ij}=kT^{ij}, \quad k=\frac{8\pi G}{c^4}
\tt \tag{Eq3.3-7}
\]
この様にしてアインシュタインはエネルギー・運動量テンソル:T と整合の取れた重力方程式にたどり着いた。これをもって一般相対性理論の完成となり、近代物理学の到達した最高点といえる。
Post Views: 4
 質量が大きいほど、線の数が多い。 質量は重力線を供給する源泉と考える。
質量が大きいほど、線の数が多い。 質量は重力線を供給する源泉と考える。
 重力は重力ポテンシャルφを創る。重力(加速度)を積分すると重力ポテンシャルとなる。
重力は重力ポテンシャルφを創る。重力(加速度)を積分すると重力ポテンシャルとなる。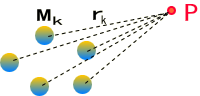





コメント