本編は一般相対性理論1 [一般座標変換編] から続いての、一般相対性理論の解説となる。
一般相対性理論では曲がった時空を扱うためにテンソルやリーマン幾何等の数学知識が必要になる。ここではベクトルの平行移動よる曲率の定義と重力理論に必要となるリーマン幾何学のいくつかを解説する。引き続き可能なかぎり数式処理 (CAS) を使って視覚化を行い、直観的な理解を助けられるようにしようと思う。本稿で使用したMathematicaのコードの解説 の方もご参考願いたい。
2.1 共変微分
前章で極座標上の2点P1-P2間を速度ベクトルを平行移動させたが、P1上にある任意をベクトルでも同じことができる。速度ベクトルと始点を合わせて括り付け、いっしょに移動させれば良い。当然クリストッフェルの係数をそのまま使える。
反変ベクトルの平行移動
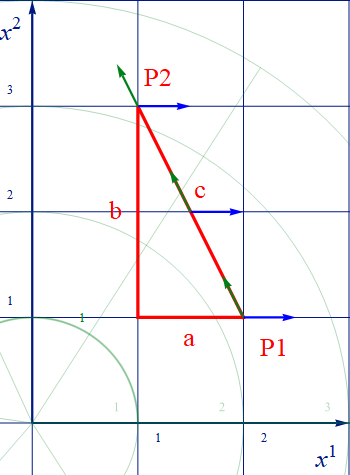
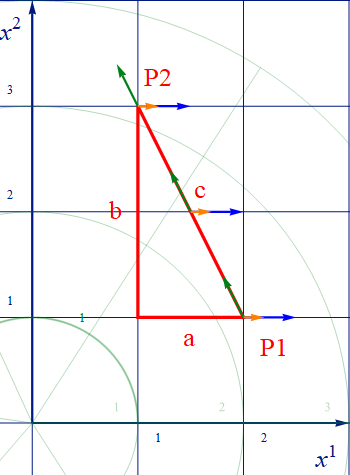
例えば以下の様にP1-P2間上に、速度ベクトルとは別の何かの、例えば座標の微小変位量を表す反変ベクトル(青)が有ったとしよう。さらに前章での仮想実験で使用した速度ベクトル(緑)はP1からP2に真っすぐ向かっているので、始点を重ねて描く以下の様になる。これはまだ移動させていない。『それぞれ3箇所に青と緑のベクトルが在る』という状況設定をしただけだ。
図2.1-1
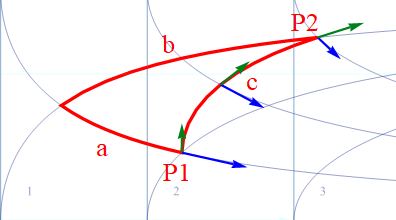
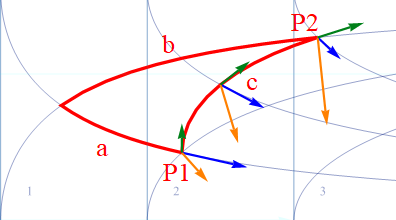
この3組のベクトルを u系から見ると、以下の様に見える。
図2.1-2
繰り返しになるが、これはまだベクトルの移動させているわけでは無く、単に u系からx系を眺めただけだ。尚、緑の速度ベクトルは前章【ベクトルの平行移動 】で解説した以下の運動方程式を満たしている。
\[\small
\begin{cases}
[x系]\space\large\frac{d^2 x^i}{d t^2}\small =0\\\\
[u系]\space\large\frac{d^2 u^i}{d t^2}+\left(\frac{\partial u^i}{\partial x^n}\frac{\partial ^2x^n}{\partial u^j\partial u^k}\right)\frac{du^j}{dt}\frac{du^k}{dt}\small =0
\end{cases}
\tt \tag{Eq2.1-1}
\]
さて、いよいよ出発点P1上にある青ベクトルを u系上で速度ベクトルと同時に移動させてみよう。以下はベクトルの前章での平行移動の方程式(Eq1.3-6 )だ。上記Eq2.1-1の下段の式と同じものだ。速度ベクトルの平行移動として解釈した記述となっており、カッコで囲った部分が係数部 Γ に対応する。尚、Eq2.1-1での対称性によりj、kはどちらでも良い。
\[\small
V^i-V^i\scriptsize //\space\small=\Gamma^i_{\space jk}\Delta u^j V^k
\]
緑の速度ベクトルを移動させるためには Δu=Vとして(Δu=V.Δt であるが、Δt=1 としてある)微小距離 Δu の移動を繰り返しP2に到達させた。したがって
\[\small
(\Gamma^i_{\space jk}\Delta u^j )
\]
を反変ベクトルである青ベクトルAの平行移動でもそのまま利用でき、方程式は
\[\small
A^i-A^i\scriptsize //\space\small=(\Gamma^i_{\space jk}\Delta u^j) A^k
\tt \tag{Eq2.1-2}
\]
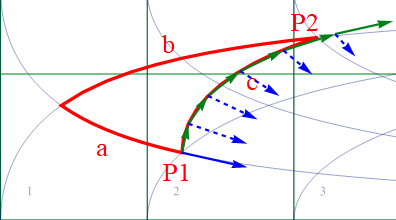
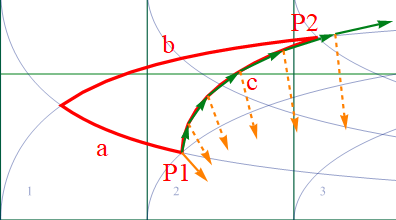
となる。つまり、速度ベクトルと青ベクトルで始点を括り付け、(Γi jk Δuj )を共通に使うと両者の各区間での微小変位が同時に計算できる。 図1.3-4 は速度ベクトルを泳がせる仮想実験であったが、上記の式を加えて同じ条件で実施してみよう。おおざっぱに言うと Δu にP1-P2間を5分割した大きさを設定してある。
図2.1-3
移動させた青ベクトルを点線で表示しよう。上記の通り、青ベクトルが速度ベクトルと一緒になって移動していくことが確認できる。経路を5分割して繰り返し数を抑えたので精度が低く、最後のベクトルの始点がP2から少しずれている。
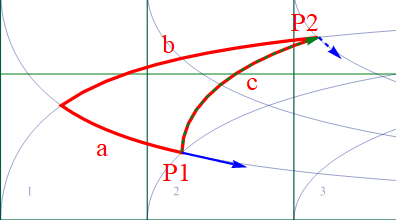
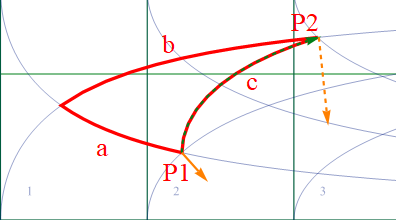
経路分割を100に増やして(つまりΔuは1/100)精度を上げると、以下の様にP2に正しく到達する。この点線青ベクトルは図2.1-1の実線青ベクトルと等しい。尚、緑の速度ベクトルは100分割されると小さすぎるので、個別の表示を省いている。
図2.1-4
ここであらためて強調しておくが、図2.1-4のP2の青ベクトルは元々P1に有った青ベクトルをEq2.1-2の式を使って平行移動させたものだ。それがP2既存の青ベクトルと一致することを、この仮想実験で確認している。
共変ベクトルの平行移動
任意の反変ベクトルは、同じ反変ベクトルである速度ベクトルと同様にEq2.1-2を使って平行移動させることができた。共変ベクトルの場合は以下の様に修正する必要がある。(係数において、ベクトルと縮約する添字の位置と符号がが+になっていることに注意)
\[\small
B_k-B_k\scriptsize //\space\small=-(\Gamma^i_{\space jk}\Delta u^j) B_i
\tt \tag{Eq2.1-4}
\]
共変ベクトルの一例としてスカラー場の傾斜を考えよう。
\[\small
E(x)=a x^1
\]
何らかのスカラー量 E が x1 方向に上り斜面状に傾斜分布している。ベクトルBを以下に様に定義すると、x系におけるE場の量の傾きを示す共変ベクトルとなる。
\[\small
B_k=\frac{\partial E(x)}{\partial x^k}
\]
ここで傾き a を適当にとると以下のオレンジのベクトルとして表すことができる。x1 方向に等しく上っているので、すべての点で同じ大きさの右方向の矢印となり、青の反変ベクトルと重なっている。
図2.1-4
これを座標変換しu系で眺めてみよう。x系での分布の定義 E(x)=ax におけるxをu 系に座標変換しE’(u)を得、それを u で微分し傾斜ベクトルを得れば良い。
\[\small
B’_k=\frac{\partial E'(u)}{\partial u^k}
\]
結果をプロットすると以下の図の通り。反変ベクトルと重ならなくなった。変換により新しい座標での各ベクトルの成分比 u1 :u2 が定まるが、共変ベクトルBの成分は場の微分であるので座標変位の逆数に比例する。従って反変ベクトルとの成分比が変わってしまい、矢印の向きがずれてしまう。尚、方向がずれても3点でそれぞれ内積 Ai Bi は同じに保とうとしていること(雰囲気?)が分かるだろうか?それぞれの点で両ベクトルが絶妙にバランスを取って内積の値を一定に保っている様子が何となく分かるる。x系では3点での内積は同じ様に設定してあった。座標変換で内積は不変量であるので、それが理解しやすい事例と言えるかもしれない。
図2.1-5
以下はP1の共変ベクトルを線分cを5分割し、係数を計算しながら平行移動させた結果だ。やはりP2では少しずれている。
図2.1-6
100分割して移動させると、正しくP2に到達しベクトルは図2.1-5と一致する。
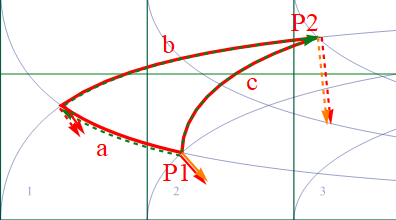
今までの移動は全て最短経路c経由であった。遠回り経路 a-b の場合も本方程式が機能することを確認しておこう。直通経路cに対し、a-b 経路は赤いベクトルとしよう。経路 a の終点で移動対象の共変ベクトルを複製し経路bの始点にセットし直せばよい。
図2.1-7
図2.1-8
上記の通り、結果どちらの経路でもP2に到達すると等しくなっている。
任意の経路でのベクトルの平行移動
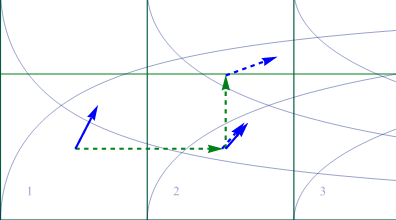
以上は測地線に沿っての移動であった。もちろん任意のu系上の任意の経路を使っても問題ない。以下の様に反変ベクトルを下経路で移動させたものと、
図2.1-9
以下の様に、上コース(赤いベクトル)で移動させたものは一致する。
図2.1-10
速度ベクトルと異なり、この様な任意のベクトルの移動自体に物理的な意味は無い。ただし、ベクトルを平行移動を定義することにより少し離れた位置にある別のベクトルと比較が可能になったという事だ。
曲がった空間では、空間に分布する量の微分が単純に定義できない。図2.1-2の様に直交直線系では同じ大きさのベクトルが曲線座標系では少し離れると大きさが違って見えるからだ。
しかし2点間のベクトルにおいてどちらかを平行移動させ、もう一方のベクトルと重ねて差分を取れば、微分が定義できることになる。
以上のことをEq2.1-2(u座標の記述を厳密に書いた)を使って整理すると、
\[\small
\begin{cases}A^i\scriptsize //(u+\Delta u)\space\small=A^i(u)-(\Gamma^i_{\space jk}\Delta u^j) A(u)^k\\\small
\quad \Updownarrow\\\small
A^i(u+\Delta u)
\end{cases}
\]
上記の式で、微小変位Δuを無限小変位uに置き換えるて差分を取り、無限小変位duで割ると
\[\small
\frac{A^i(u+d u)-A^i(u)+\Gamma^i_{\space jk}d u^j A(u)^k}{du}\\\small
=\frac{A^i(u+d u)-A^i(u)}{du}+\Gamma^i_{\space jk} A(u)^k
\]
となる。この第1項は通常の微分の定義そのものであり、第2項は歪みの補正項と言える。これを基にして、以下のように曲線座標系におけるベクトルの微分をコロンを使って定義する。
\[\small
A^i:_j\equiv\frac{\partial A^i}{\partial u^j}+\Gamma^i_{\space jk} A(u)^k
\]
共変ベクトルの場合は Eq2.1-4 より、
\[\small
B_k:_j\equiv\frac{\partial B_k}{\partial u^j}-\Gamma^i_{\space jk} B(u)_i
\]
リーマン幾何学では、これを共変微分と呼ぶ。以降、微分表記の簡素化のため通常微分をカンマを使って 以下の様に書こう。
\[\small
A^i,_j\equiv\frac{\partial A^i}{\partial u^j}
\]
2.2 曲率
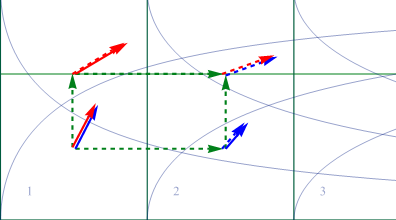
前節で使ったx系は2次元直交直線座標であり、平らな空間で歪んでいない。u系の方は曲線座となる極座表であり、確かに測地線は曲がっていたが、空間自身は平らな空間であった。その場合のベクトルの平行移動経路による差分は図2.1-10の通り無かった。
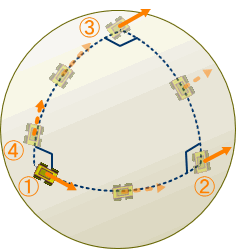
しかし我々は球面ではそれが一致しないことを知っている。例えば何処かの小さな惑星(地球は海が多い)で車を赤道上の地点①から赤道沿いに東に走らせよう。その時、車の進行方向に矢印を取り付けておこう。やがて車は東に経度で90度走らせ地点②に到着する。ハンドルを90度左に切るとると北極点を向く。先ほどまで進行方向を指していた矢印を、90度右に回して取り付け直しておこう。そのまま真っすぐ北上すると、やがて北極点の③に到着する。
図2.2-1
北極点に到着すると、90度左にハンドルを切る。その時、元の方向を保つためにには矢印を右に90度回して取り付け直さな変えればならない。そしてその時点で図の通り矢印は車の後ろを向いていることになる。
さて、そのまま南下すると最初の地点①に戻ってくることになるが、出発時と比べて矢印は90度左にずれてしまっている。これは球面が歪んだ空間であることに起因する。
そこでこの後、我々が手に入れたベクトルの平行移動の方程式を使って、球面の歪みを定式化することが次の目標となる。
空間に分布するベクトルAを2回続けて j, k により共変微分することを考る。この時 j, kの順番を変えて差分を取ると空間の歪みに応じて結果は0とは限らなくなる。
\[\small
A^i_{\space :jk}-A^i_{\space :kj}\equiv R^i_{ljk}A^l
\]
この係数Rをリーマン・クリストッフェルの曲率テンソル(以降、曲率と略す)と呼び、共変微分における微分順序の違いによりベクトルやテンソルの成分に生じる差を表す。つまり共変微分は可換では無いという事だ。
具体的にこのリーマン曲率Rを求めてみよう。
正順 j->k とするとしよう。そうすると、まず(Ai :j ) に対して k の共変微分を適用する。(Ai :j ) は反変成分i 、共変成分j を持つ混合テンソルとみなせるので、接続係数の項には以下の様にそれぞれ+Γ -Γ が対応する。
\[\small
(A^i_{\space:j})_{:k}=(A^i_{\space:j }),_{\space k}+\Gamma^i_{hk}(A^h_{\space:j })-\Gamma^h_{jk}(A^i_{\space:h })
\]
(Ai :j ) を共変微分で展開すると
\[\small
=(A^i_{\space,\space j }+\Gamma^i_{jl}A^l
),_{\space k}+\Gamma^i_{hk}(A^h_{\space,\space j }+\Gamma^h_{jl}A^l)-\Gamma^h_{jk}(A^i_{\space:h })
\]
積の微分に注意しさらに展開すると、以下の通り正順の結果を得る。
\[\small
(A^i_{\space:j})_{:k}=A^i_{\space,\space j k}+\Gamma^i_{jl,k}A^l +\Gamma^i_{jl} A^l,_k
+\Gamma^i_{hk}A^h_{\space,\space j }+\Gamma^i_{hk}\Gamma^h_{jl}A^l-\Gamma^h_{jk}(A^i_{\space:h })
\]
逆順 k->jに関しては以下の通り、kとjを入れ替えれば良い。正順と等値の項にアンダーラインを引いた。
\[\small
(A^i_{\space:k})_{:j}=\underline{A^i_{\space,\space kj}}+\Gamma^i_{kl,j}A^l +\underline{\Gamma^i_{kl} A^l,_j}
+\underline{\Gamma^i_{hj}A^h_{\space,\space k }}+\Gamma^i_{hj}\Gamma^h_{kl}A^l-\underline{\Gamma^h_{kj}(A^i_{\space:h })}
\]
Ai ,ji と Γh kj (Ai :h ) は k, j に関する対称性により等値となる。
正順から逆順を引き残った項を整理する。
\[\small
A^i_{\space :j:k}-A^i_{\space :k:j}\\\small
=\Gamma^i_{jl,k}A^l -\Gamma^i_{kl,j}A^l
+\Gamma^i_{hk}\Gamma^h_{jl}A^l-\Gamma^i_{hj}\Gamma^h_{kl}A^l\\\small
=(\Gamma^i_{jl,k}-\Gamma^i_{kl,j}
+\Gamma^i_{hk}\Gamma^h_{jl}-\Gamma^i_{hj}\Gamma^h_{kl})A^l \quad\space
\]
結果、以下の曲率を得る。
\[\small
A^i_{\space :j:k}-A^i_{\space :k:j}=R^i_{ljk}A^l\space ,\quad\quad\quad\quad \\\small
R^i_{ljk}=\Gamma^i_{jl,k}-\Gamma^i_{kl,j}
+\Gamma^i_{hk}\Gamma^h_{jl}-\Gamma^i_{hj}\Gamma^h_{kl}
\tt \tag{Eq2.2-1}
\]
赤道付近でのベクトルの移動経路差実験
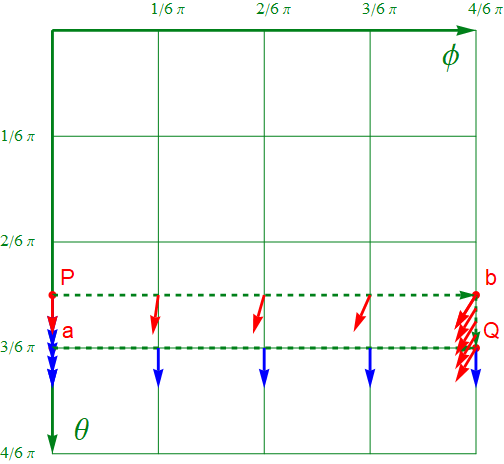
2次元極座標と同様にベクトルの平行移動を試してみよう。下側を通る青コース[P-a-Q]と、上側を通る赤コース[P-b-Q]で比較してみる。
以下の図2.2-2はu系:θ-φ平面に左下のPから右上Q点への反変ベクトルを平行移動させた結果のプロットである。適当な大きさの微小変位ベクトルをP点に用意した。
図2.2-2
図2.1-10と異なり青ベクトルと赤ベクトルは重ならなくなってしまった。
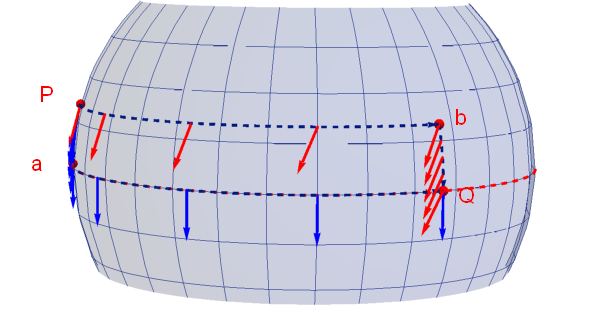
3次元空間よりこれを眺めてみよう。こちらは、x系に相当する。u系の住人から認識することのできない神様視点となる。
図2.2-3
今回の図2.2-3で分かる通り赤道付近を移動させていた。P-a-Q-bが囲む面積に注目しておいてほしい。そこそこの多さがある。そして赤、青ベクトルの差は大きい。
北極付近でのベクトルの移動経路差実験
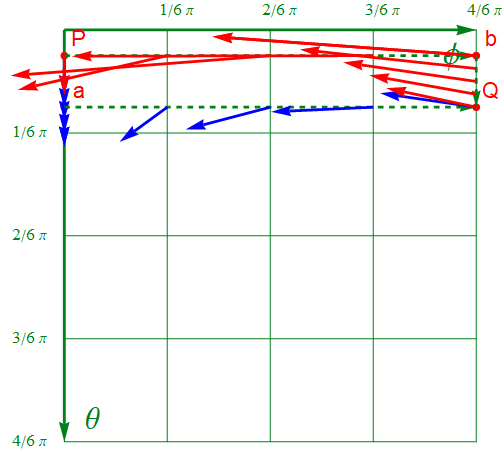
次に北極点付近を同じ様に移動させてみよう。図2.2-4がその結果となる。
u系でP-a-Q-bが囲む見かけの面積は図2.2-2の物と同じだ。極地近辺ではφ方向の目盛りが詰んでいるのでベクトルの大きさの変化が激しい。
図2.2-4
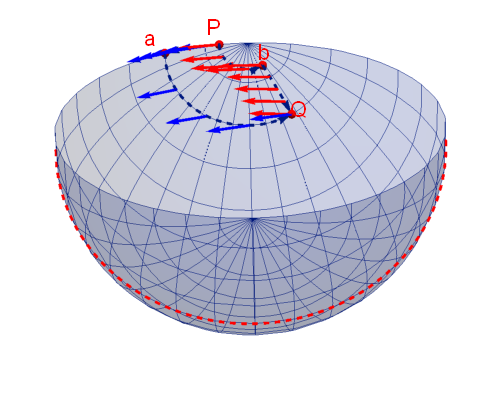
これをx系3次元上の視点で確認してみる。当然u系と異なりベクトルの大きさの変化は見られない。平行移動の条件としてベクトルの大きさを不変であるとしていた事を思い出してほしい。u系での移動範囲は赤道の場合と同じだが、御覧の通りx系におけるP-a-Q-bが囲む面積はかなり小さくなった。同様にQ点に到達した青ベクトルと赤ベクトル差も小さくなっている。
図2.2-5
このことよりベクトルの経路差はu系ではなく、x系における移動経路の大きさと関係していることが理解できる。移動範囲をどんどん小さくして、局所的な範囲で解析してみよう。クリストッフェルの係数を座標位置 u の関数とし\(\small \Gamma^i_{jk}(u)\)となり、その近傍では1次のテーラー展開で適用可能となる。尚、以下の議論は2次元平面の住人の視点であることに注意。
[下側 aルート]:以下の通り、P点から\(\small u^1\) (つまりθ軸)のみを微小変位させてa点に平行移動させる。固定のダミーインデックスは単純なスカラーどうしの積を指定しており、他の指標が表すベクトルやテンソル全体に掛かるスカラーの係数となる。
\[\small
A^i(P)_{//a}=A^i(P)-\Gamma^i_{\color{red}{1}k}(P)\Delta u^\color{red}{1}A^k(P)
\]
\(\small \Delta u^1\) はスカラーとなり\(\small \Delta_1\)と記述する。
\[\small
A^i(P)_{//a}=A^i(P)-\Gamma^i_{\color{red}{1}k}(P)\Delta_\color{red}{1}A^k(P)
\]
次に、a からQは以下の通り\(\small \Delta u^2\) (φ軸)のみを変位させての移動となる。この式の\(\small
A^i(P)_{//a} \)に上記を代入する。
\[\small
A^i(a)_{//Q}=A^i(P)_{//a}-\Gamma^i_{\color{blue}{2}k}(a)\Delta_\color{blue}{2} A^i(P)_{//a}\\\small
=\left[A^i(P)-\Gamma^i_{\color{red}{1}k}(P)\Delta_\color{red}{1}A^k(P)\right] \quad\quad\quad\quad\\\small
\quad-\Gamma^i_{\color{blue}{2}k}(a)\Delta_\color{blue}{2}\left[A^k(P)-\Gamma^k_{\color{red}{1}h}(P)\Delta_\color{red}{1}A^h(P)\right]
\]
さらに\(\small\Gamma^i_{\color{blue}{2}k}(a)\)を微小区間P-aにおいて1次のテーラー展開で近似する。
\[\small
=\left[A^i(P)-\Gamma^i_{\color{red}{1}k}(P)\Delta_\color{red}{1}A^k(P)\right] \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\\small
-\left[\Gamma^i_{\color{blue}{2}k}(P)+\Gamma^i_{\color{blue}{2}k}(P)_{,\color{red}{1}}\Delta_\color{red}{1}\right]\Delta_\color{blue}{2}\left[A^k(P)-\Gamma^k_{\color{red}{1}h}(P)\Delta_\color{red}{1}A^h(P)\right]
\]
カッコを展開。 全ての係数ΓはPの関数となったので(P)を省略し、Aを括り出す準備のためAのダミーインデックスをhに統一。
\[\small
=A^i-\Gamma^i_{\color{red}{1}h}A^h \Delta_\color{red}{1}
-\Gamma^i_{\color{blue}{2}h}A^h\Delta_\color{blue}{2}\quad\quad\quad\quad\\\small
-\Gamma^i_{\color{blue}{2}h,\color{red}{1}}A^h\Delta_\color{red}{1}\Delta _\color{blue}{2}+\Gamma^i_{\color{blue}{2}k}\Gamma^k_{\color{red}{1}h}A^h\Delta_\color{red}{1}\Delta_\color{blue}{2}\\\small
+\Gamma^i_{\color{blue}{2}k,\color{red}{1}}\Gamma^k_{\color{red}{1}h}A^h\Delta_\color{red}{1}\Delta_\color{red}{1}\Delta_\color{blue}{2}
\quad\quad\quad\quad\space\space
\]
最後の項は2次の微小変位Δ1 Δ1 を含むので無視できるので式より除き、以下の様に括り出し整理する。
\[\small
A^i_{//a//Q}
=\left\{A^i-\Gamma^i_{\color{red}{1}h}A^h \Delta_\color{red}{1}
-\Gamma^i_{\color{blue}{2}h}A^h\Delta_\color{blue}{2}\right\}\\\small
\quad\quad\quad+\left[\Gamma^i_{\color{blue}{2}k}\Gamma^k_{\color{red}{1}h}-\Gamma^i_{\color{blue}{2}h,\color{red}{1}}\right]A^h\Delta_\color{red}{1}\Delta _\color{blue}{2}
\]
上記{}内は移動コース対称の項であるので、この後下側のbルートの結果を引くと消去される。
[上側 bルート]:上記の固定添字1と2を入れ替えればよい。
\[\small
A^i_{//b//Q}
=\left\{A^i-\Gamma^i_{\color{blue}{2}h}A^h\Delta_\color{blue}{2}-\Gamma^i_{\color{red}{1}h}A^h \Delta_\color{red}{1}\right\}\\\small
\quad\quad\quad+\left[\Gamma^i_{\color{red}{1}k}\Gamma^k_{\color{blue}{2}h}-\Gamma^i_{\color{red}{1}h,\color{blue}{2}}\right]A^h\Delta_\color{red}{1}\Delta _\color{blue}{2}
\]
aルートからbルートを引き、係数部を曲率Eq2.2-1と同じ順番に整理する。
\[\small
A^i_{//a//Q}-A^i_{//b//Q}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\space\space
\\\small
=\left[\Gamma^i_{\color{red}{1}h,\color{blue}{2}}-\Gamma^i_{\color{blue}{2}h,\color{red}{1}}
+\Gamma^i_{\color{blue}{2}l}\Gamma^l_{\color{red}{1}h}-\Gamma^i_{\color{red}{1}l}\Gamma^l_{\color{blue}{2}h}
\right]A^h\Delta_\color{red}{1}\Delta_\color{blue}{2}\\\small
=R^i_{h12}A^h\Delta_1\Delta_2=R^i_{hjk}A^h\Delta_1 x^j\Delta_2 x^k
\\\small
\]
Δu1 、Δu2 はu系で直交するように選んだので経路が囲む微小面積を表している。対応するx系における微小面積一般の平行四辺形の面積求め方と同様に、Δ1 xj 、Δ2 xk の外積(クロス積) (Δ1 xj )×(Δ2 xk )のノルムとして求めることができる。つまり、図2.2-5の移動範囲を微小にすると、3次元上の点Pにおける微小平行四辺形の形をした接平面と見なしせ、(Δ1 x1 )×(Δ2 x2 )は接平面から直立したベクトルとなり、その大きさが微小面積ΔSを表していると考えられる。(尚今回の球面の例では、平行四辺形は長方形となる)
尚、参考書によっては青コースと赤コースの順番が逆になって、Rの符号が逆に定義されているものがある。見分け方として、Rの添字kがクリストッフェル係数の微分で+の項側に出てくるかーの項側に出てくるかの差となる。
曲率テンソルRに関する実験
r=1の球面
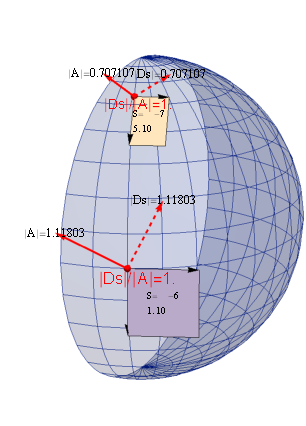
曲率に関するいくつか実例を示そう。r=1の球面で赤道(θ=π/2)と北極点寄り(θ=π/6)でu系で同じ大きさのベクトルAを置き、両者を比較する。
u系でそれぞれ微小変位Δ1=Δ2=0.001を与えて球面における曲率テンソルRを基に、以下の様にベクトルの変化量 \(\small \widetilde{D}=R.A.Δ_1Δ_2 \)を計算する。尚、この後ベクトルの成分に関して、\(\small \widetilde{D}\)はu系側、\(\small \overline{D}\)はx系側というように区別しよう。
\[\small
\widetilde{D}^i=
R^i_{h12}\widetilde{A}^h\Delta u^1
\Delta u^2=
\Delta_1\Delta_2\left[\begin{array}{c} 0&-sin^2(u^2)\\1&0 \end{array}\right]\widetilde{A}^h
\]
\(\small \Delta_1 \Delta_2\)はスカラー係数であり括り出され、曲率の残りの成分 \(R^i_h\) はベクトル\(\small \widetilde{A}\)に掛かる2階のテンソルとなる。
x系3次元上のベクトルAの変化量を表すベクトルを\(\small \overline{D}\)とすると\(\small
\overline{D}^i=\frac{\large \partial x^j}{\large \partial u^j}\widetilde{D}^j\)となる。
上記を計算しこの変化量をプロットしてみよう。経路の囲む微小面積に相当するΔ1 Δ2 は10-6 となるので、Dは非常に小さい値だ。描画時にはΔ1 Δ2 で割ってスケールを戻したい。しかし変化量はu系側の見かけの面積ではなくx系における経路面積に比例することが予想されていた。
そこでu系での微小面積量 Δ1Δ2ではなくx系での微小面積に相当するS=|(Δ1×1)×(Δ2×2)|で割ってスケールを戻してみよう。推測が正しければ補正後の経路差の変化量 \(\small |\overline{Ds}|=|\overline{D}|/S \)は球面の位置に依存しなくなるはずだ。
尚、当然x系3次元上のベクトル\(\small \overline{A}\)は任意の大きさと向きを与えて良いがu系より\(\small
\overline{A}^i=\frac{\large \partial x^j}{\large \partial u^j}\widetilde{A}^j\)と変換してプロットする必要がある。結果は以下の通り。
まず、下側の赤道(θ=π/6 )に位置するベクトルの表示で|A|=1.118となっているが、点線の矢印で示された変化量ベクトル|Ds |も同じ値となっている。つまり経路差比率 |Ds |/|A|=1 である。この点における微小面積S=1. 10-6 となっており、極座標での赤道における計量は局所的にデカルト座標と同じだ。
次に上側はθ=π/6 での計算結果だ。面積S=5. 10-7 となっていおり、赤道の1/2となって理論値と合っている。ベクトルAはu系において赤道点のものと同じ大きさと方向を与えたのだが計量の変化により、|A|=0.707と小さくなっている。これに対しSで割って補正した経路差変化量ベクトル|Ds |も同じ量を示しており、比率 |Ds |/|A|は 1 である。つまりベクトルの移送経路における経路差は経路の囲む面積に比例することが確認できた。
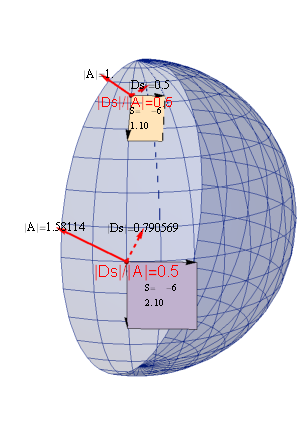
r=√2の球面
続いて球の大きさrを√2倍にして同様の計算を行ってみよう。以下の通り、u系でのベクトルの大きさを変えていないので、x系におけるベクトルAは計量の変化により√2倍になっている。
しかし経路差比率|Ds |/|A|はどちらも0.5となっている。つまり半径が大きくなり、それにより球面の曲率が小さくなったことで経路差の変化量が半分になったと解釈できる。
以下は本稿で使用したMathematicaのコードの解説です。
[CAS-Lab] ブラックホールをあなたの手の上に 一般相対性理論2
リーマン幾何学で記述された、曲がった空間でのベクトルの動きなどの数式は難解で、その意味するところを直観的に理解することが難しいと思う。本稿に沿って、自分で処理を確認しながら実行することにより、その数式の意味を実感できるようになると思う。
Post Views: 6






コメント