本編は特殊相対性理論3から続いての、一般相対性理論の最初のノートとなる。
宇宙論やブラックホールなどを理解しようとすると一般相対性理論を理解しなければならない。しかし一般相対性理論では曲がった時空を扱うためにテンソルやリーマン幾何等の数学知識が必要になる。数式を追いかけるだけでは実感がわかないだろう。そこで本稿では可能なかぎり数式処理 (CAS) を使って視覚化を行い、直観的な理解の助けにしようと思う。
1 等価の原理
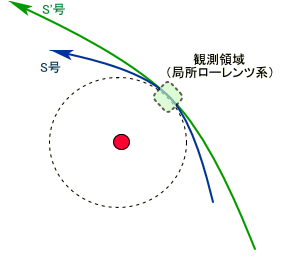
アインシュタインの有名な思考実験にロープの切れたエレベーターの話がある。自由落下しているエレベーターの中では光は直線に進むことを観察することになるだろう。なぜならエレベーターの中は力学的にも物理全般的にも無重力の宇宙空間における慣性系と区別をつける方法が見当たらない。しかし地上からエレベーターの中を観察している人にはエレベーターの中の光は他の全ての物体とともに加速されながら落ちてゆくのを見るとこになる。そしてその軌跡は放物線を描くことになりローレンツ変換で扱えない。
もう少しこの思考実験を続けてみよう。いまあなたは宇宙船の実験室にいる。ロケットエンジンが止まっているので加速度を感じない。この状態では特殊相対性理論で行ったローレンツ収縮や時間の遅れなどのローレンツ変換にまつわる実験をもう一つの慣性運動中の実験室ロケットとの間で行うことができる。
さらに慣性系の定義を拡大して、地球の重力圏で自由落下していたとしてもすれ違う近傍で、局所的にローレンツ変換の実験ができるだろう。
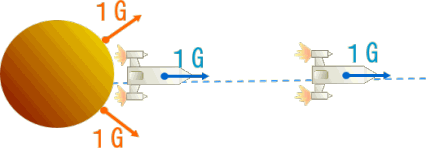
次に、自由落下している実験室ロケットが(地球に衝突するのが嫌だから)逆噴射をして落下速度を減らし始めたとする。
逆噴射加速度を重力加速度=9.8m/s2と同じにしよう。あなたは地表と同じ重力を宇宙船内で感じることになる。
あなたの宇宙船が地表すれすれに達して、落下速度がちょうど0になったとする。着地まで1mほど残して地表の重力とロケットのが逆噴射加速度が均衡し、その状態で動かなくなったとしよう。あなたは宇宙船の窓から外の景色を眺めて宇宙船が着地したのかと勘違いするかもしれない。
あなたもさることながら、物理学的にもロケットが着地した状態と、このように1mほど浮いている状態と区別はつけられないだろう。だからあなたは地表に立っている観測者と同じに立場になる。
もしロケットの速度が速すぎて、遠く地球の重力圏外から逆噴射しなければならなくても同じことになる。つまりあなたは遠く地球が見えないうちから逆噴射で重力が発生していたとして、その間ずっと地表に着いたかどうかは、ロケットが地面に接触したことを直接目視するまで区別がつかないという事だ。
上記の思考実験が等価の原理の背景だ。重力系と加速系は実験室内の様に局所かぎると物理原理的に区別がつかないだろうという発想だ。アインシュタインは特殊相対性理論で(光の軌跡が時空上45度で真っすぐ進む)慣性系間での変換を明らかにしたが、次のステップとして(光の軌跡が時空上真っすぐ進まない)加速系が扱える変換を発見し、重力が働いている系(つまり地上の人)どのように記述できるかを明らかにすることになる。以上が一般相対性理論のあらすじとなる。
2 曲がった座標系
特殊相対性理論2 [不変量編]では直線座標間の変換を扱った。球面など曲がった空間を扱うためにはリーマン幾何学が必要となるが、その場合曲線座標を理解する必要がある。まずは2次元から初めて見よう。尚、上記 [不変量編] ではいろいろな座標変換と不変量に関する解説がなされている。ぜひ事前に一読されたい。
座標変換の一般化
これまでは線形変換による座標変換を例にとって解説してきた。以下の様に座標変換用の行列Cを座標位置ベクトルxに作用させて、新しい座標位置ベクトル u を得るという式のスタイルだ。
\[\small
\begin{cases}\bf u=C\cdot x\\
\bf x=C^{-1}\cdot u
\end{cases}
\]
アインシュタインの縮約規則で書くと
\[\small
\begin{cases}
u^{i}=C^{i}_{j}x^{j}\\
x^{i}=(C^{-1})^i_jx^{j}
\end{cases}
\]
曲線座標への変換では、もはやこのスタイルが取れない。二次元を例とすると、以下の様に変換、逆変かを関数化することになる。
\[\small
\begin{cases}u^{i}\equiv u^{i}(x^1,x^2)\\
x^{i}\equiv x^{i}(u^1,u^2) \end{cases},\quad i=1, \space 2
\tt \tag{Eq1.2-1}
\]
以下の特殊相対性理論2(Eq2.3-14)の計量の求め方と同様だ。
まず、\(\small (\mathbf{ C }^{-1}\cdot\Delta \mathbf{ u })^2 \) の自乗部をベクトルの内積として表現したが、行列演算の作法に基づき、もう少し丁寧に記述しておこう。\(\small \boldsymbol{d x}=\left(\begin{array}{c}dx^1\\dx^2 \end{array} \right) ,\space \boldsymbol{d u}=\left(\begin{array}{c}du^1\\du^2 \end{array} \right)\) とすると、距離の自乗は、
\[\small
ds^2=\bf du^t(C^{-1})^t \space (C^{-1}) d u\\ \small
=\left(\begin{array}{c}du^1&du^2 \end{array} \right)
\left(\begin{array}{c}\frac{\partial x^1}{\partial u^1}&\frac{\partial x^2}{\partial u^1}\\ \frac{\partial x^1}{\partial u^2}&\frac{\partial x^2}{\partial u^2}\end{array}\right)
\left(\begin{array}{c}\frac{\partial x^1}{\partial u^1}&\frac{\partial x^1}{\partial u^2}\\ \frac{\partial x^2}{\partial u^1}&\frac{\partial x^2}{\partial u^2}\end{array}\right)
\small \left(\begin{array}{c}du^1\\ \\du^2 \end{array} \right)
\]
\(\small (\mathbf{ C }^{-1}\cdot\Delta \mathbf{ u })^2 \) の自乗部をベクトルの内積として表現したが、行列演算の作法に基づき、もう少し丁寧に記述してみよう。\(\small u=\left(\begin{array}{c}u^1\\u^2 \end{array} \right) \) とすると、距離の自乗は、
\[\small
d s^2=\boldsymbol{d u^t \space g \space d u }
\]
計量行列を抜き出して書くと、
\[\small
\boldsymbol{g}=
\left(\begin{array}{c}\frac{\partial x^1}{\partial u^1}&\frac{\partial x^2}{\partial u^1}\\ \frac{\partial x^1}{\partial u^2}&\frac{\partial x^2}{\partial u^2}\end{array}\right)
\left(\begin{array}{c}\frac{\partial x^1}{\partial u^1}&\frac{\partial x^1}{\partial u^2}\\ \frac{\partial x^2}{\partial u^1}&\frac{\partial x^2}{\partial u^2}\end{array}\right)
\]
成分で書くと
\[\small
d s^2= g_{ij}d u^i d u^j ,\\
\small g_{ij}=\sum_{n=1}^{2}\frac{\partial x^n}{\partial u^i}\frac{\partial x^n}{\partial u^j}
\tt \tag{Eq1.2-2}
\]
この式の示すように、計量は位置により変化するので、指定した座標の近傍でしか使えない。それでは実際に、これを曲線座標変換に使ってみよう。
極座標変換
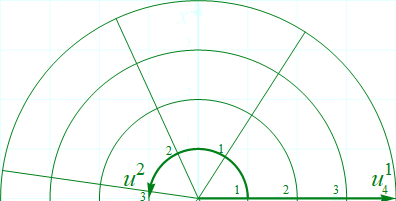
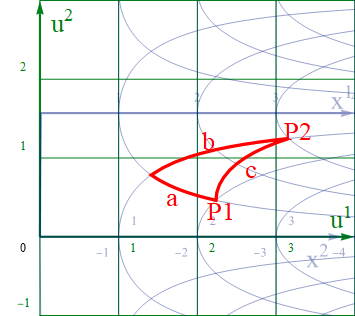
直交直線座標をX系とし、極座標をU系とし、双方からの変換がどうなっているかを調べてみる。以下の図1.2-1は極座標の半円分を表示してある。これをU系とし、は動径を u1 、偏角を u2 する。
図1.2-1
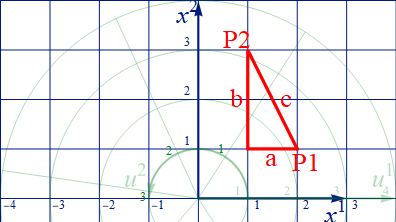
この極座標を直交直線座標のX系に重ねてみよう。 X系には以下の様な線分 P1-P2 を斜辺とする直角三角形が描かれている。
図1.2-2
U系への変換式は以下通りだ。
\[\small
\begin{cases}u^1=\sqrt{(x^1)^2+(x^2)^2} \\
u^2=sign(x^0)\cdot\arccos{\large \frac{x^1}{\sqrt{(x^1)^2+(x^2)^2}}} \end{cases}
\tt \tag{Eq1.2-3}\]
逆変換の式は以下の通り。
\[\small
\begin{cases}x^1=u^1\space \sin{(u^2)}\\
\small
x^2=u^1\space\cos{(u^2)}\end{cases}
\tt \tag{Eq1.2-4}
\]
U系に移って、上記逆変換の式を使ってX系を眺めてみよう。
図1.2-3
この様に、X系の座標は奇妙な曲線を描き、三角形はゆがんでしまう。U系の世界からX系に描かれた線分の長さを知る方法を考えてみよう。
まずは逆変換の式 Eq1.2-4 に対し Eq1.2-1 を使って計量を求める。
参考までに
\[\small
\delta_{kl}\frac{\partial x^k}{\partial u^i}\frac{\partial x^l}{\partial u^j}
\tt \tag{Eq1.2-5}
\]
を以下の様に偏微分の係数1組分の行列に分けて積の形にすると、計算全体の見通しがよいかもしれない。右に偏微分の係数1組分を書き、左にその転置を置く。
\[\small
\left(\begin{array}{c}\frac{\partial x^1}{\partial u^1}&\frac{\partial x^1}{\partial u^2}\\ \frac{\partial x^2}{\partial u^1}&\frac{\partial x^2}{\partial u^2}
\end{array}\right)^{\large t}
\small
\left(\begin{array}{c}\small1&\quad \small0\\ \\\small 0\space &\quad\small1 \end{array}\right)
\left(\begin{array}{c}\frac{\partial x^1}{\partial u^1}&\frac{\partial x^1}{\partial u^2}\\ \frac{\partial x^2}{\partial u^1}&\frac{\partial x^2}{\partial u^2}
\end{array}\right)
\tt \tag{Eq1.2-6}
\]
真ん中はδでX系がピタゴラスの定理が成り立つユークリッド空間であることを意味している。単位行列なので無視でき、以下の行列の積を計算すればよい。
\[\small
\left(\begin{array}{c}\frac{\partial x^1}{\partial u^1}&\frac{\partial x^2}{\partial u^1}\\ \frac{\partial x^1}{\partial u^2}&\frac{\partial x^2}{\partial u^2}
\end{array}\right)
\left(\begin{array}{c}\frac{\partial x^1}{\partial u^1}&\frac{\partial x^1}{\partial u^2}\\ \frac{\partial x^2}{\partial u^1}&\frac{\partial x^2}{\partial u^2}
\end{array}\right)
\tt \tag{Eq1.2-7}
\]
行列の積を取ると以下の通り。
\[\small
\left(\begin{array}{c}
\frac{\partial x^1}{\partial u^1}\frac{\partial x^1}{\partial u^1}
+\frac{\partial x^2}{\partial u^1}\frac{\partial x^2}{\partial u^1}&
\frac{\partial x^1}{\partial u^1}\frac{\partial x^1}{\partial u^2}
+\frac{\partial x^2}{\partial u^1}\frac{\partial x^2}{\partial u^2}
\\
\frac{\partial x^1}{\partial u^2}\frac{\partial x^1}{\partial u^1}
+\frac{\partial x^2}{\partial u^2}\frac{\partial x^2}{\partial u^1}&
\frac{\partial x^1}{\partial u^2}\frac{\partial x^1}{\partial u^2}
+\frac{\partial x^2}{\partial u^2}\frac{\partial x^2}{\partial u^2}
\end{array}\right)
\tt \tag{Eq1.2-8}
\]
それでは実際に極座標の逆変換式より1組の偏微分行列をを求めてみよう。
\[\small\left(\begin{array}{c}
\frac{\partial }{\partial u^1}u^1\space \sin{(u^2)}&
\frac{\partial }{\partial u^2}u^1\space \sin{(u^2)}\\
\small
\frac{\partial }{\partial u^1}u^1\space \cos{(u^2)}&
\frac{\partial }{\partial u^2}u^1\space \cos{(u^2)}
\end{array}\right)
\\
\small
=\small\left(\begin{array}{c}
\sin{(u^2)}&\cos{(u^2)} \\
\small
u^1\space \cos{(u^2)}& -u^1\sin{(u^2)}
\end{array}\right)
\]
これを転置行列と積を取ると極座標の計量が以下の様に求まる。
\[\small
\small
\boldsymbol{g}=\small\left(\begin{array}{c}
\sin{(u^2)}&\cos{(u^2)} \\
\small
u^1\space \cos{(u^2)}& -u^1\sin{(u^2)}
\end{array}\right)
\left(\begin{array}{c}
\sin{(u^2)}&u^1\space \cos{(u^2)}\\
\small
\cos{(u^2)}& -u^1\sin{(u^2)}
\end{array}\right)
\\
=\small\left(\begin{array}{c}
1& 0\\0&(u^1)^2
\end{array}\right)
\tt \tag{Eq1.2-9}
\]
動径が大きな位置では、偏角の値が小さく読めるので、それを補償していることが分かる。
この計量を使って、U系にいたまま、斜辺cの本来の長さ(X系における長さ)を求めてみよう。
計量が場所によって変わってくるので、指定した座標の近傍でしか使えないという事を実感できるように、あえて数値処理で求めてみる。
以下の計算式のようにP1-P2間を n 分割し、各点で計量 gi を計算し、その点から次の点までの線分に適用し、長さの合計を取る。
\[\small
s^{2}=\sum_{i=1}^{n}\boldsymbol{g}_i\cdot \Delta \boldsymbol{u}_i\cdot \Delta \boldsymbol{u}_i
\]
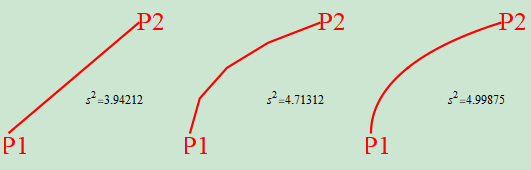
計算結果は以下の図1.2-4の通りだ。
図1.2-4
まず、1番目は分割なしでP1での計量をP2までの線分に適用したものだ。約3.9であり誤差が大きい。2番目は4分割したものだ。約、4.7と多少誤差が小さくなっている。最後は1000分割したものだ。ほぼX系における長さ s2=5 を再現できたと言って良いだろう。
この様に、曲線座標系では計量は座標の関数となっている。
3 ベクトルの平行移動
さてエレベーターの思考実験に戻ろう。われわれは重力場の中で光はどう進むのかを解明する必要がある。ここに『エレベーターの中では光は直線だった。しかし地表からみたら曲がって見えた』という状況はこの極座標と直交直線座標間の変換関係:『X系ではP1-P2間は直線であった。しかしU系からみたら曲がって見えた』と同じだ。
そこで曲がった空間U系で光の進行をベクトルの平行移動としてとらえてみよう。X系で直線上を平行移動(直進)しているベクトルをU系で見ると曲線をなぞってベクトルが移動して見えるという様にだ。
X系で質点が外力が加わらず、したがって慣性で直線運動していたとする。そうすると運動方程式は以下の通り。
\[\small
\frac{d^2 x^i}{d t^2}=0
\tt \tag{Eq1.3-1}
\]
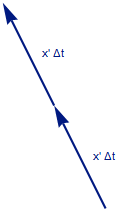
これは図1.2-2のP1からP2への線分上を、以下の様に速度ベクトル x’ が真っすぐに微小距離 x’Δt を平行移動しているとみることができる。
図1.3-1
一方、定義よりxは以下の通りu(t)の合成関数である。
\[\small
x^{i}\equiv x^{i}(u^1,u^2)
\tt \tag{Eq1.3-2}
\]
したがって一般の数学公式集に有るように以下の合成関数の微分の公式がそのまま使える。
[一階微分]
\[\small
\frac{dx^n}{d t}=\frac{\partial x^i}{\partial u^n}\frac{du^n}{d t}
\]
[二階微分]
\[\small
\frac{d^2 x^n}{d t^2}=\frac{\partial x^i}{\partial u^n}\frac{d^2 u^n}{d t^2}+\frac{\partial ^2x^i}{\partial u^j\partial u^k}\frac{du^j}{dt}\frac{du^k}{dt}
\]
上記二階微分微分の公式を使ってEq1.3-1は以下の通りとできる。
\[\small
\frac{\partial x^i}{\partial u^n}\frac{d^2 u^n}{d t^2}+\frac{\partial ^2x^i}{\partial u^j\partial u^k}\frac{du^j}{dt}\frac{du^k}{dt}=0
\]
さらに第一項の偏微分部 \(\small \partial x^i/\partial u^n\) の逆関数( \(\small \partial u^i/\partial x^n\)と逆行列になっている)をとって第二項に移せる。
\[\small
\frac{d^2 u^i}{d t^2}+\frac{\partial u^i}{\partial x^n}\frac{\partial ^2x^n}{\partial u^j\partial u^k}\frac{du^j}{dt}\frac{du^k}{dt}=0
\tt \tag{Eq1.3-3}
\]
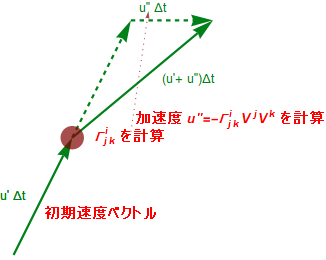
これがU系における質点の慣性運動を表す方程式だ。実感しやすいように時間微分に関する項を加速度αと速度Vに書き換えてみた。尚、V(t)の前の du/dt はこの後 Δt をかけて微小変位と解釈するために残しておく。
\[\small
\alpha(t)^i=-\frac{\partial u^i}{\partial x^n}\frac{\partial ^2x^n}{\partial u^j\partial u^k}\frac{du^j}{dt} V(t)^k
\tt \tag{Eq1.3-4}
\]
上記の式は『座標点が指定されると以下の座標相互の変換関数でのみ決まる係数部 Γ が速度ベクトルに掛かる』と解釈できる。
\[\small
\frac{\partial u^i}{\partial x^n}\frac{\partial ^2x^n}{\partial u^j\partial u^k}\equiv\Gamma^i_{\space jk}
\tt \tag{Eq1.3-5}
\]
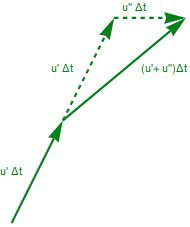
これは『U系では座標の歪みにより、速度ベクトルの大きさに、座標位置により決まった上記の係数 を乗じた加速度 u’’ が生じる。その結果、以下の u”Δt の様に(見かけの)力が働き速度ベクトルの方向が図1.2-3の P1-P2 の線分に沿って移動して行く』とも解釈することができる。
図1.3-2
2番目のベクトルを1番目のベクトルが Δu だけ平行移動したものだとして V//と表そう。そうすると上記の運動方程式視点の解釈をベクトルの平行移動という視点で解釈し直すことができEq1.3-4は
\[\small
V^i-V^i\scriptsize //\space\small=\Gamma^i_{\space jk}\Delta u^j V^k
\tt \tag{Eq1.3-6}
\]
と表現できる。
さてこの後、重力理論を構築するためにはEq1.3-4を計量gを使って書き表す必要がある。
まず Eq1.2-2 の計量を以下の様に見通しを良くするため簡略化しよう。δの非対角要素は0なのでn=mの要素のみでよく、mを省略した。さらにユークリッド計量であるのでδも省略した。ミンコフスキー計量の場合は残しておく必要があるが、いずれにせよこの後の変形に影響は無い。
\[\small
g_{ij}=\delta_{mn}\frac{\partial x^m}{\partial u^i}\frac{\partial x^n}{\partial u^j}\\\small
=\sum_{n=1}^{2}\delta_{nn}\frac{\partial x^n}{\partial u^i}\frac{\partial x^n}{\partial u^j}\\\small
=\sum_{n=1}^{2}\frac{\partial x^n}{\partial u^i}\frac{\partial x^n}{\partial u^j}
\tt \tag{Eq1.3-7}
\]
これをさらに u で微分をする。積の微分(*1)で以下の様に二つの項になる。指標[ i, j, k ]を以下の様に入れ替えて三つの式を書き出した。左辺は微分表記の簡素化のため微分に使う指標をカンマの後ろに表記してある。
\[\small
g_{ij},_{\space k}=\sum_{n=1}^2\left(\frac{\partial^2 x^n}{\partial u^i \partial u^k}
\frac{\partial x^n}{\partial u^j}
+\frac{\partial^2 x^n}{\partial u^j \partial u^k}\frac{\partial x^n}{\partial u^i}\right)
\\ \small
g_{kj},_{\space i}=\sum_{n=1}^2\left(\frac{\partial^2 x^n}{\partial u^k \partial u^i}
\frac{\partial x^n}{\partial u^j}
+\frac{\partial^2 x^n}{\partial u^j \partial u^i}\frac{\partial x^n}{\partial u^k}\right)
\\ \small
g_{ik},_{\space j}=\sum_{n=1}^2\left(\frac{\partial^2 x^n}{\partial u^i \partial u^j}
\frac{\partial x^n}{\partial u^k}
+\frac{\partial^2 x^n}{\partial u^k \partial u^j}\frac{\partial x^n}{\partial u^i}\right)
\]
以下の式の通り、1番目と3番目を足して2番目の式を引き、2で割ると以下の様に Eq1.3-5 に似た感じの係数を得る。
\[\small
\frac{1}{2}(g_{ij},_{\space k}+g_{ik},_{\space j}-g_{kj},_{\space i} ) \\ \small
=\sum_{n=1}^2\frac{\partial^2 x^n}{\partial u^j \partial u^k}\frac{\partial x^n}{\partial u^i}\\\scriptsize あるいは、\quad\quad\quad\quad \\\small
=\delta_{mn}\frac{\partial^2 x^m}{\partial u^j \partial u^k}\frac{\partial x^n}{\partial u^i}
\tt \tag{Eq1.3-8}
\]
この係数部は以下の式の通り第1種クリストッフェルの三指標記号として定義されている。
\[\small
\Gamma_{ijk}
\equiv\frac{1}{2}(g_{ij},_{\space k}+g_{ik},_{\space j}-g_{kj},_{\space i} )
\tt \tag{Eq1.3-9}
\]
運動方程式様のEq1.3-4はこの第1種クリストッフェル係数を使うと、以下の様に変える必要がある。
\[\small
g_{ij}\alpha(u)^j=-\frac{\partial x^i}{\partial u^n}\frac{\partial ^2x^n}{\partial u^j\partial u^k}v(u)^j v(u)^k\\\small
=\Gamma_{ijk}\space v(u)^j v(u)^k
\tt \tag{Eq1.3-10}
\]
この様に(見かけの力による)加速度に計量を掛けて使う必要がある。そこであらたに、以下の計量を定義する。
\[\small
g^{ij}=\delta^{mn}\frac{\partial u^i}{\partial x^m}\frac{\partial u^j}{\partial x^n}\\\small
=\sum_{n=1}^{2}\frac{\partial u^i}{\partial x^n}\frac{\partial u^j}{\partial x^n}
\tt \tag{Eq1.3-11}
\]
これは gij の逆行列になっている。これを使って Eq1.3-10 の一階微分部を反転させをると以下の様になる。
\[\small
g^{i\space l}\Gamma_{ljk}=\sum_{n=1}^2\frac{\partial u^i}{\partial x^n}\frac{\partial u^l}{\partial x^n}
\frac{\partial^2 x^n}{\partial u^l \partial u^k}\frac{\partial x^n}{\partial u^i}
\\ \small
=\frac{\partial^2 x^n}{\partial u^j \partial u^k}\frac{\partial u^i}{\partial x^n}
=\Gamma^i_{jk}
\tt \tag{Eq1.3-12}
\]
これで 曲線座標系における質点の慣性運動を表す方程式 Eq1.3-5 と同じ式を得ることができた。つまり以下がEq1.3-5の計量を使った定義となる。
\[\small
\Gamma^i_{jk}
\equiv \frac{1}{2}g^{in}(g_{nj},_{\space k}+g_{nk},_{\space j}-g_{kj},_{\space n} )
\tt \tag{Eq1.3-13}
\]
Eq1.3-12から理解できることだが、jとkは入れ替え可能であり対称性がある。この式は第2種クリストッフェルの三指標記号と呼ばれて、Eq1.3-4前後の議論より、曲線座標におけるベクトルの平行移動を定めている。
従ってこの式を使えば、計量さえ定まっていればx座標における運動方程式等を使わずに、曲線座標上を速度ベクトルを移動させることができる。尚、今回直観的理解のしやすさを優先してユークリッド空間での説明となったので計量の定義には δ を使ったが、ミンコフスキー時空(擬ユークリッド空間)の場合は η となる。
実感いただけるよう、図1.3.2のベクトル加算を Eq1.3-4 を数値処理することによりプロットしてみよう。
以下の図の様にP1 でのベクトルの初期の方向と速度だけ与える。以降、『移動先の計量を使ってクリストッフェルの係数を計算し、その係数を現在の速度ベクトルに適用して加速度を得て、次の速度ベクトルを計算する』を繰り返す。
図1.3-3
以上の算法を数式を使って表す。
微小変位 Δu=V Δt だが簡単のため微小時間 Δt=1と単位時間とする。
P1-P2 区間の距離は\(\small \sqrt{5}\)であり、これを m分割する場合は、x系における初期速度\(\small \overline{V}(0)=x'(0)=\sqrt{5}/m\)と置けばよい。
極座標変換式 Eq1.2-3 を\(\small u^i=U^i(x^j) \)、逆変換を\(\small x^i=X^i(u^j) \)、x系における初期速度を\(\small \overline{V}\)とすると、初期値は以下の通りとなる。
\[\small
u(0)=U[x(0)], \space\space \Delta u(0)=V(0)=\frac{\partial u}{\partial x}\overline{V}(0)
\]
u系の V(0) は上記の通り、変換して求める。
これを、以下をの算法での初期値(n=0)に与えて、以降nを m回カウントアップしながら、計算を繰り返す
\[\small
\begin{cases} \alpha^i(n)=\Gamma^i_{\space jk}[u(n)]\Delta u^j (n)V^k(n)\\ \\\small
V^i(n+1)=V^i(n)+\alpha^i(n)\\ \small
\Delta u^i(n+1)=V^i(n) \space \Delta t, \quad \Delta t=1\\ \\ \small
u^i(n+1)=u^i(n)+\Delta u^i(n)
\end{cases}
\]
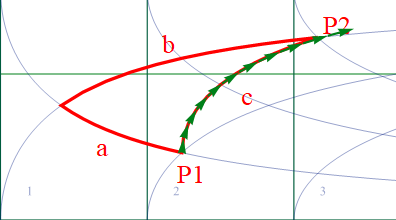
以下の図のように勝手に曲線座標を泳いでいってくれる。これはm=10の例であり、加速度計算までを10回分繰り返している。
図1.3-4
最後のベクトルの始点がP2に一致することが目標だが、やはり10分割では粗い様で少しずれてしまっている。あらためて言うが、曲線座標系では計量やクリストッフェルの係数は場所の関数となっているので局所的にしか適用できない。少し離れると距離に応じた誤差が生じる。この様に局所的であるという事がどのようなことかが実感できたと思う。
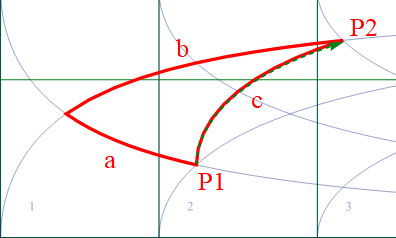
分割を細かくするにはΔu(=V.Δt) を小さくする必要がある。速度を小さくするか、Δtを小さくするかだ。ここではΔt は単位時間としておき、Vの方を小さくて繰り返しを増やそう。100回にした場合以下の図のようにほぼ線分は重なり、P2と一致している。(Vは小さくなったので個別の矢印表示を省略した)
図1.3-5
注目しておいてほしいことは、この図を描く上で図1.3.1の様なX系の質点の運動方程式を必要としていないと言うことだ。これは、この後重要な道具立てとなる。
尚、以上のu系における挙動をx系で観察するためには\(\small \overline{V}(n)=\frac{\large \partial
x}{\large\partial u} V(n) \)追加するだけでよいのだが、結果はつまらないものになりそうだと、容易に想像できるので省略した。
球面上のベクトル移動
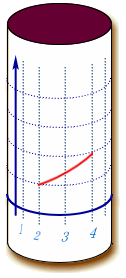
曲がった平面に進んでみよう。今までの議論は2次元空間に極座標を張った場合に関してである。座標は確かに曲がっていて、計量が場所によって変化していたが、二次元空間(平面)自体は平らであった。いつでも直交直線座標を張り直すことができる。座標は曲がっているが、歪んでいない。
一見歪んでいそうな円筒の表面だが、グラフ用紙をはりつけることができ、歪んでいる2次元空間とは言えない。
しかし球の表面はそうはいかない。無理やり表面にグラフ用紙を貼り付けようとしても、しわが寄ってうまくいかない。
貼り付けるためにはゴムシートの様なもので、無理やりひきのばして貼り付けるしかない。
理由として球面では円周率が2πより小さくなっている。従って紙を接地させた点からの半径方向の長さに対して直交する円周方向の長さが縮んでいるので余分な部分が出てくるからだ。この様に円筒と異なり、球面は歪んだ2次元空間だ。
一見関係ないように思えるが、空間の歪みとベクトルの平行移動はにおける挙動は密接な関係にある。歪んだ空間(リーマン空間)の入り口として、球面上でのベクトルの平行移動を試してみよう。
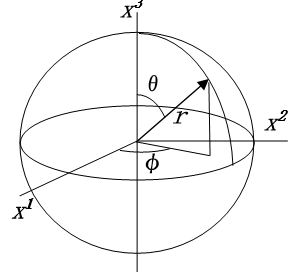
球面上の位置は3次元極座標使うとうまく表すことができる。3次元直交直線座標と関係は以下の図の通となる。動径のr軸を固定すると球面が決まる。そして緯度に相当するθと経度に相当するφで球面上の1点が指定できる。
図1.3-6
r:u1, θ:u2, φ:u3 とすると、直交直線座標X系への変換は以下の式となる。
\[\small
\begin{cases}x^1=u^1\space \sin{(u^2)}\cos{(u^3)}\\
\small
x^2=u^1\space\sin{(u^2)}\sin{(u^3)}\\
\small
x^3=u^1\space\cos{(u^2)}\end{cases}
\tt \tag{Eq1.3-14}
\]
球面を[ θ:u2, φ:u3] の二次元空間として計量を求めてみよう。rは次元ではなくパラメータとなるため、偏微分の行列 [∂x/∂u] は以下の通り3行2列となる。
\[\small
\frac{\partial x^{1:3}}{\partial u^{2:3}}=
\left(
\begin{array}{cc}
{u^1} \cos ({u^2}) \cos ({u^3}) & -{u^1} \sin ({u^2}) \sin ({u^3}) \\
{u^1} \cos ({u^2}) \sin ({u^3}) & {u^1} \sin ({u^2}) \cos ({u^3}) \\
-{u^1} \sin ({u^2}) & 0 \\
\end{array}
\right)
\]
偏微分の行列 [∂x/∂u] t・[∂x/∂u] をEq1.2-5~Eq1.2-7を参考に計算すると、以下の2行2列の計量を得る。
\[\small
\boldsymbol{g}=
\left(
\begin{array}{cc}
(u^1)^2 & 0 \\
0& (u^1)^2\sin^2(u^2) \\
\end{array}
\right)
\tt \tag{Eq1.3-15}
\]
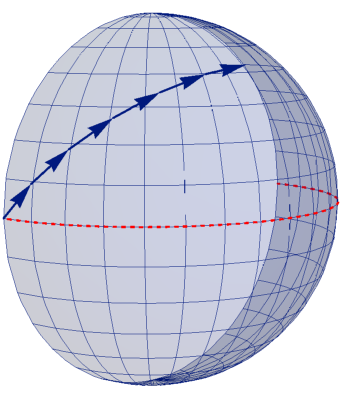
この計量を使って r=1 とした球面をなす3次元空間にベクトルを泳がせてみよう。計算方法は図1.3-3と同様だ。
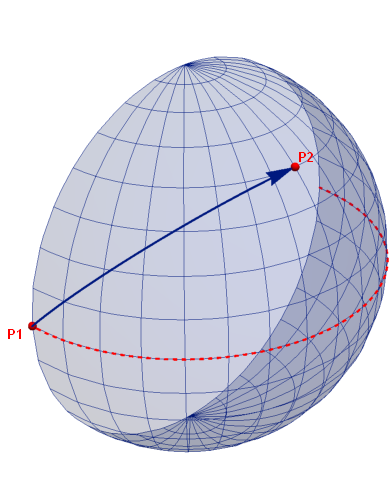
φ-θ成分で[π/√2,π/√2]となる初期速度ベクトルを設定し、Δtを1/6として、r=1 固定で3次元ベクトルをクリストッフェルの係数を使って計算を6回繰り返している。この様に3次元空間に埋め込まれた球面(半分に切ってある)を速度ベクトル(正確には微小距離Δs=v Δt)が平行移動してして行くことが確認できる。
図1.3-7
ベクトルの起点の接平面上に矢印を引き、終点から垂線を落とした地点を新たな起点とすべきところだろうが、本図では手抜きして3次元空間で始点、終点間をを直接矢印でつないでいる。(つまり少しだけ地面を潜っているが絵ずらは同じ)
さて、この球面上のベクトル移動を我々は3次元空間から眺めている。しかし地球表面と同じで、球面に張り付いた人にとって次元rは存在しない。したがって、認識できる次元である緯度に相当するθと、経度に相当するφを使って地表の位置を表すことにしよう。
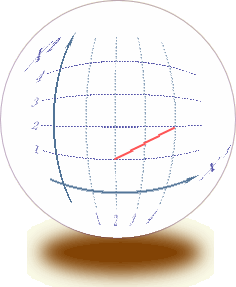
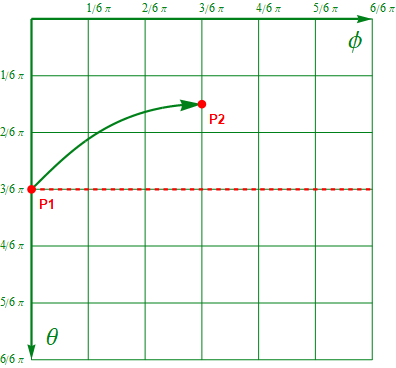
この2次元座標であるφ-θ平面上に先ほどのベクトルの移動経路をプロットしたものが以下の図となる。赤道にあたる位置に赤い点線を引いてある。
図1.3-8
ご承知の通り、この作図方法は地図で言うメルカトル図法と同じものだ。メルカトル図法の欠点は赤道付近と極付近とで地形の大きさが全然違ってくる。
例えば極付近にあるグリーンランドは大陸に近い大きさに見えるが実際はそんなに大きくはない。これは計量(Eq1.2-5)を見てみると、2行目の通り、θ (=u2) が小さい領域ではφ (=u3) 方向の目盛りが詰んでいるので、読み取った値を小さくする補正がなされていることで理解できる。
4 測地線
さて、前述の2次元極座標で慣性運動する速度ベクトルを泳がせると、軌跡 P1-P2 は曲線となるが、直交直線座標では直線であった。今回も軌跡 P1-P2 はφ-θ平面上で曲線となるが、3次元直交直線座標上の軌跡は曲がっている。もちろん3次元の球面上であるから、これは仕方がない。
図1.4-1
じつはこの速度ベクトルの軌跡は測地線と呼ばれ、歪んだ空間におけるP1-P2間の最短経路を示している。東京-サンフランシスコ間の航路がメルカトル図では大円を描き遠回りしている様に見えても、実際は最短経路であり、その距離を示していることと同じだ。
球面の場合は割と測地線をイメージしやすいが、図形が複雑になると難しくなる。参考までに同じことをトーラス(ドーナッツ形)で試してみた。ドーナッツの穴の方と外側では歪みが異なり、球面より複雑だ。
このように測地線はドーナッツに巻き付いていく。
測地線方程式の導出
測地線の求め方は解析力学で確立されているので、そちらからの求め方もなぞっておこう。
既に議論の様に、我々は既にP1-P2間の距離が2次元空間における2次元極座標の場合でも、3次元空間における球面の2次元極座標の場合でも、最短になる経路の求め方を知っている。
『P1より一定の大きさの速度ベクトルにクリストッフェルの係数かけて微小時間づつ平行移動させて行き、P2にたどり着いたらそれが最短経路であり測地線だ』このイメージを頭にとどめながら測地線方程式の導出を確認してみよう。
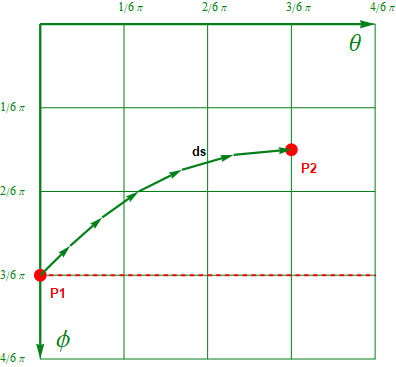
vdtは微小移動距離を表している。距離なのでそれをdsとしよう。これは線分の構成要素なので線素と呼ぶ。以下の図の様にP1-P2間の経路は無限小の線素:dsが集まってできていると考える。(図1.2-4も参照)
図1.4-2
P1-P2間の経路長をlとすると、
\[\small
l=\int_{p1}^{p2}ds, \quad \quad \\
\small
ds=\sqrt{g_{jk}(u)du^j du^k}
\]
と書くことができる。このP1-P2間の経路(線分)の形状を定める関数を\(\small f(u) \)としよう。そうすると線分長 \(\small l\) は\(\small f(u) \) をパラメータとした関数 \(\small l(f(u)) \) と考えられる。
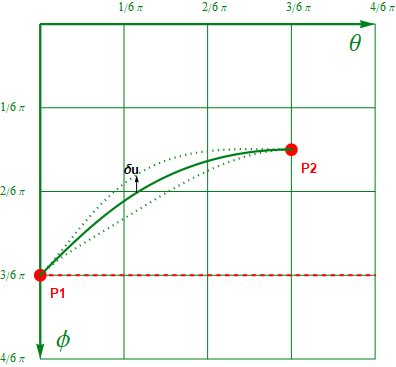
仮に 以下の図で緑の実線の\(\small f(u) \) が目的の測地線(最短距離)であったとする。
図1.4-3
それに対し、上記の図の様に微小変形 \(\small \delta \) を与え、点線の形状になったとしよう。その場合、経路上の各線素
\[\small
g_{jk}(u)du^jdu^k=ds^2\\
\]
は、
\[\small
g_{jk}(u+\delta u)d(u^j +\delta u^j)d(u^k+\delta u^k)=d(s+\delta s)^2\\
\]
となる。
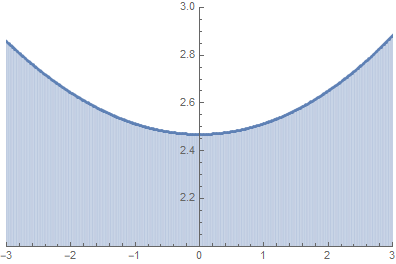
ここで図1.4-3と同じ形状の適当なベジェ曲線を使い、実際に測地線に微小変形与えてみよう。P1-P2間の自乗距離 l と変形の大きさの関係をプロットすると以下の様になる。
図1.4-4
横軸が δuで縦軸が自乗距離だ。変形 0 で極小点を持ち、理論値 \(\small \pi^2/4\)となっている。これから数式を変形してゆくが、上記の極小点\(\small dl/du=0\) となる条件が線分長lの最小距離となる経路だ。
まず、両辺全てを展開しよう。極値条件を求めるため極値近傍(極値である測地線にδの微小変形を試みている)での展開となるのでδの二乗以降は無視できる。計量部は以下の様に2次までテイラー展開しておく。
\[\small
g_{jk}(u+\delta u)=g_{jk}(u)+\frac{\partial g_{jk}(u)}{\partial u^h}\delta u^h +\space \cdot\cdot\cdot
\]
結果として、以下を得る。
\[\small
\underline{g_{jk}(u)du^j du^k}+\frac{\partial g_{jk}(u)}{\partial u^h}\delta u^h du^j du^k+2g_{jk}(u)du^j d\delta u^k\\\small
=\underline{ds^2}+2d s\space \delta ds
\]
変形前の項にアンダーラインを引いた。残りの項が変形で生じた項であり、以下に書き出す。
\[\small
\frac{\partial g_{jk}}{\partial u^h}\delta u^h du^j du^k+2g_{jk}du^j d\delta u^k=2d s\space \delta ds
\]
2右辺を微小変化にのみ関する項にし以下の様にdsを整理する。
\[\small
\left( \frac{1}{2}\frac{\partial g_{jk}}{\partial u^h}\delta u^h \frac{du^j}{ds}\frac{du^k}{ds}+g_{jk}\frac{du^j}{ds} \frac{d\delta u^k}{ds} \right) ds=\delta ds
\]
両辺をP1-P2間にわたり積分すると右辺は距離の微小変化のみを示す項となる。
\[\small
\int_{p1}^{p2}\left( \frac{1}{2}\frac{\partial g_{jk}}{\partial u^h}\delta u^h \frac{du^j}{ds}\frac{du^k}{ds}+g_{jk}\frac{du^j}{ds} \frac{d\delta u^k}{ds} \right)ds=\int_{p1}^{p2}\space \delta ds
\]
極小点であるのでdl/du=0の条件より
\[\small
\int_{p1}^{p2}\space \delta ds=0
\]
であるので以下の等式を得る。
\[\small
\int_{p1}^{p2}\left( \frac{1}{2}\frac{\partial g_{jk}}{\partial u^h}\delta u^h \frac{du^j}{ds}\frac{du^k}{ds}+g_{jk}\frac{du^j}{ds} \frac{d\delta u^k}{ds} \right)ds=0\\ \small
\downarrow
\\ \small
\int_{p1}^{p2} \frac{1}{2}\frac{\partial g_{jk}}{\partial u^h}\delta u^h \frac{du^j}{ds}\frac{du^k}{ds}ds+\int_{p1}^{p2}g_{jk}\frac{du^j}{ds} \frac{d\delta u^k}{ds}ds=0
\]
第2項を\(\small \frac{\large du^j}{\large ds} \)と\(\small \frac{\large d\delta u^k}{\large ds}\)に分けて部分積分\(\scriptsize{(*2)}\)する。
\(\\\)
*1 関数の積の微分
(f・g)’=f’・g+f・g’
*2 部分積分法
積の微分を変形する。
f’・g=(f・g)’-f・g’
積分する。
∫(f’・g)dx=f・g-∫(f・g’)dx
\[\small
\int_{p1}^{p2} \frac{1}{2}\frac{\partial g_{jk}}{\partial u^h}\delta u^h \frac{du^j}{ds}\frac{du^k}{ds}ds+
\begin{bmatrix} g_{jk}\large\frac{d u^j}{ds} \small\delta u^k \end{bmatrix}^{p2}_{p1}-
\int_{p1}^{p2} \frac{d}{ds}\left(g_{jk}\frac{d u^j}{ds} \right)\delta u^kds=0
\]
\(\scriptsize
\begin{bmatrix} g_{jk}\frac{ du^j}{ ds} \delta u^k \end{bmatrix}^{p2}_{p1}
\)の部分は両端P1、P2の近傍で滑らかな変形を前提とすると\(\small \delta u(p1)=0, \space \delta u(p2)=0\)より消去される。
\[\small
\int_{p1}^{p2} \frac{1}{2}\frac{\partial g_{jk}}{\partial u^h}\delta u^h \frac{du^j}{ds}\frac{du^k}{ds}ds-
\int_{p1}^{p2} \frac{d}{ds}\left(g_{jk}\frac{d u^j}{ds} \right)\delta u^k ds=0\]
第2項の積の微分を展開する。さらに第2積分項におけるダミー添字 “k” を “h” に振り直し、δu をかっこ外に括り出す。(計量 g が対称行列なので gjhvjwh のような場合、gjhの j-h を入れ替えてもよい)
\[\small
\int_{p1}^{p2} \frac{1}{2}\frac{\partial g_{jk}}{\partial u^h}\delta u^h \frac{du^j}{ds}\frac{du^k}{ds}-
\int_{p1}^{p2} \left(\frac{dg_{jk}}{ds}\frac{du^j}{ds}+g_{jk}\frac{d^2 u^j}{ds^2} \right)\delta u^k ds=0\\ \small
\downarrow\\ \small
\int_{p1}^{p2} \left(\frac{1}{2}\frac{\partial g_{jk}}{\partial u^h}\frac{du^j}{ds}\frac{du^k}{ds}-
\frac{dg_{jh}}{ds}\frac{du^j}{ds}-g_{hj}\frac{d^2 u^j}{ds^2}\right) \delta u^h ds=0
\]
δu は任意の変形であるから、等式が恒等的に成り立つためには、以下の様に被積分項は 0 でなければならない。
\[\small
\frac{1}{2}\frac{\partial g_{jk}}{\partial u^h}\frac{du^j}{ds}\frac{du^k}{ds}-
\frac{dg_{jh}}{ds}\frac{du^j}{ds}-g_{hj}\frac{d^2 u^j}{ds^2}=0\\\small
\]
さらにdg/dsを偏微分に変形し、du/dsを括りだし整理を進めると
\[\small
\frac{1}{2}\frac{\partial g_{jk}}{\partial u^h}\frac{du^j}{ds}\frac{du^k}{ds}-
\frac{\partial g_{jh}}{\partial u^k}\frac{du^j}{ds}\frac{du^k}{ds}-g_{hj}\frac{d^2 u^j}{ds^2}=0\\\small
\downarrow
\]
\[\small
\left(\frac{1}{2}\frac{\partial g_{jk}}{\partial u^h}-
\frac{\partial g_{jh}}{\partial u^k}\right)\frac{du^j}{ds}\frac{du^k}{ds}-g_{hj}\frac{d^2 u^j}{ds^2}=0\\\small
\]
かっこ内第1項は j-k に対称であるので、第2項をhを固定して j-k を入れ替えた2つの項に分解する。
\[\small
\frac{1}{2}\left(\frac{\partial g_{jk}}{\partial u^h}-
\frac{\partial g_{jh}}{\partial u^k}-\frac{\partial g_{hk}}{\partial u^j}\right)\frac{du^j}{ds}\frac{du^k}{ds}-g_{jh}\frac{d^2 u^j}{ds^2}=0\\\small
\]
Eq1.3-9と同じ係数部を得る。
\[\small
g_{hj}\frac{d^2 u^j}{ds^2}+\frac{1}{2}\left(
\frac{\partial g_{hk}}{\partial u^j}+\frac{\partial g_{hj}}{\partial u^k}-\frac{\partial g_{jk}}{\partial u^h}\right)\frac{du^j}{ds}\frac{du^k}{ds}=0\\\small
\downarrow\\\small
g_{hj}\frac{d^2 u^j}{ds^2}+\Gamma_{hjk}\frac{du^j}{ds}\frac{du^k}{ds}
=0
\tt \tag{Eq1.4-1}
\]
左辺第1項に計量が掛かっているのでこのままでは使い勝手が悪い。両方の項に計量の逆行列を掛け
\[\small
(\underline{g^{ih}g_{hj}})\frac{d^2 u^j}{ds^2}+\frac{1}{2}g^{ih}\left(
\frac{\partial g_{hk}}{\partial u^j}+\frac{\partial g_{hj}}{\partial u^k}-\frac{\partial g_{jk}}{\partial u^h}\right)\frac{du^j}{ds}\frac{du^k}{ds}=0\\\small
\]
以下の式を得る。
\[\small
\frac{d^2 u^i}{ds^2}-\frac{1}{2}g^{ih}\left(
\frac{\partial g_{hk}}{\partial u^j}+\frac{\partial g_{hj}}{\partial u^k}-\frac{\partial g_{jk}}{\partial u^h}\right)\frac{du^j}{ds}\frac{du^k}{ds}=0\\\small
\downarrow\\\small
\frac{d^2 u^i}{ds^2}+\Gamma^i_{\space jk}\frac{du^j}{ds}\frac{du^k}{ds}=0
\tt \tag{Eq1.4-1}
\]
この式の係数部が第2種のクリストッフェル記号である。
以上の様にベクトルの平行移動で等速運動を曲線座標から眺めた式(合成関数の微分より求めた)と測地線方程式(最短距離からのずれをテイラー展開して求めた)は同じもので有った。
一般相対性理論はやたらと数式だらけでその記述に実感がわかないのではないかと思う。ここではベクトルの平行移動という概念を『等速運動を曲線座標から眺めてみよう!ルート』と『測地線の求め方ルート』で解説した。これは一般相対性理論という山を制覇する上で登り口に位置するものだと思うのだが、どちらがより実感がわくかと言うと、私の場合は『等速運動を曲線座標から眺めてみよう!ルート』であった。貴方は如何だっただろうか?
次の目標は曲がった空間を記述するリーマン幾何学の理解となる。
Post Views: 6