シュレディンガー方程式は相対性理論を考慮していない。したがって光速より十分小さな速度の粒子の振る舞いを記述するにとどまる。シュレディンガー方程式を特殊相対論的に整合するように改良したものがディラック方程式いう位置づけとなるが、その導出過程においてパウリ行列が重要な役目を果たすことになる。パウリ行列は時空のあらたな数学的表現であるスピノルを理解すると自然にパウリ行列の必然性が理解できる。量子論を相対性理論に適合化させたことにより、量子の持つ内部空間をの様な存在を垣間見ることが出来、なかなか興味深いものがある。
*尚、当サイトの趣旨の通り、難解な物理学でもその概念は意外とシンプルで感動を覚えるものも多く、自分なりに理解した概念の解釈を参考にしてもらえればと思い執筆している。しかし相対性理論、量子論と進み、ここに至るとその解釈にあまり自信が無い。用語の使い方も少々いい加減だと思うでそのつもりで読み進めていただきたい。
1. 四元数
四元数をイメージで言うと、複素数が2次元ベクトルを内包しているように、四元数は4次元ベクトルを内部に取り込ん四元数をイメージで言うと、複素数が2次元ベクトルを内包しているように、四元数は4次元ベクトルを内部に取り込んだ拡張複素数ようなもの言ったところだろうか?
シュレディンガー方程式は『物質を形づくる波動ψは、複素数でしか表せない量子空間に在り、その実数化した部分(ψ’.ψ) のみ我々が実体として認識できる』と言う、よくよく考えると実にとんでもない宇宙観をもたらしてくれた。この先量子論から統一理論への拡張過程で目の当たりにするだろう宇宙観の飛躍を鑑賞し堪能しようとすると、このあたりで四元数とパウリ行列を理解しておくのも良いことだろう。量子論と相対せ理論のつながりや群論との関係に対する知見が広げられる。
1.1 四元数による三次元回転演算
四元数 q の定義は複素数 z =a0 +a1 i の定義に対して、以下のように、虚数部が3個に拡張されている。( a0 , a1 , a2 , a3 )は実数、( i1 , i2 , i3 )は四元数の虚数単位。
\[\small
\begin{eqnarray}
q&=&a_0+a_1 i_1+ a_2 i_2 + a_3 i_3
\end{eqnarray}\\\
\tt \tag{Eq1.1-1}
\]
相対性理論やパウリ行列との関係を議論したいので、上記は以下のように添え字で表すことにする。
i と同じく虚数単位だ。その共役数は以下のように定められている。
\[\small
\begin{eqnarray}
q^*&=&a_0-a_1 i_1- a_2 i_2 – a_3 i_3
\end{eqnarray}
\tt \tag{Eq1.1-2}
\]
尚、a0 の後ろには “1” 隠れていて、[1 i] は複素平面の(2次元)基底、[1 i1 i2 i3 ] が4元数の(4次元)基底とみなすことができる。
本稿での四元数の表記は一般的な表記と異なるので対応以下の表にまとめた。
一般的な表記 本稿での表記 複素数の虚数単位 i h i 四元数の虚数単位 i, j, k i1 , i2 , i3
この拡張された虚数単位の演算規則は以下の通り規定されている。
\[\small
\begin{eqnarray}
i_1^2= i_2^2= i_3^2=-1
\end{eqnarray}
\tt \tag{Eq1.1-3}
\]
これは複素数の規則 i 2 =-1 と同じだ。
こちらの方は3次元の立体構造を感じられる定義といえるかも?
\[\small
\begin{eqnarray}
i_1 i_2=-i_2 i_1=i_3\\\small
i_2 i_3=-i_3 i_2=i_1\\\small
i_3 i_1=-i_1 i_3=i_2\\\small
\end{eqnarray}
\tt \tag{Eq1.1-4}
\]
これにより、
\[\small
\begin{eqnarray}
i_1 i_2 i_3=-1
\end{eqnarray}
\tt \tag{Eq1.1-5}
\]
なお、虚数単位との掛け算は
\[\small
\begin{eqnarray}
i i_1=i i_2 =i i_3=-1
\end{eqnarray}
\tt \tag{Eq1.1-6}
\]
となる。掛ける順番関しては可換。
四元数どおしの演算規則は上記の虚数単位の演算規則から分かるように非可換であったりして、複素数のそれと少し異なる。
主な演算規則:4元数 qa , qb , qc に対して
\[\small
\begin{eqnarray}
1&.&\space |q_a|^2= q_a q_a^* =\scriptsize\sum_{\mu=0}^{3}\small a_\mu^2 \\\small
2&.&\space q_a^{-1} q_a=q_a q_a^{-1}=1,\space q_a^{-1} = q_a^*/|q_a|^2\\\small
3&.&\space q_a(q_b q_c)=(q_a q_b) q_c\\\small
4&.&\space (q_a q_b)^*=q_a^* q_b^*
\end{eqnarray}
\]
複素数が複素平面(2次元)内の回転の取り扱いに優れている様に、四元数は3次元空間での回転を取り扱に優れている。
例えば、3次元空間(x,y,z)の任意の点を示す V=[v1 v2 v3 ]を回転対象とし、回転軸 R=[ r1 r2 r3 ] に対して、左に θ だけ回転させてみよう。ただしRは R2 =1 と正規化されたベクトル。Vより4元数を v=0+v1 i1 +v2 i2 +v3 i3 とし、回転軸 R からは以下の 四元数 r を作る 。
\[\small
\begin{eqnarray}
r&=&Exp[ (r_1 i_1+r_2 i_2+r_3i_3)\frac{ \theta}{2}]\\\small
\end{eqnarray}
\tt \tag{Eq1.1-7}
\]
複素指数関数のテーラー展開により奇数項と偶数項に分かれて三角関数に分解できる。分かりやすくするためにθ/2→θ, r1 =1, r2 =r3 =0 と置いと分解される様子をみてみよう。
\[\small
\begin{eqnarray}
e^{ \large i_1\theta}&=& 1+ i_1 \theta-\frac{\theta^2}{2!}-i_1 \frac{\theta^3}{3!}+\frac{\theta^4}{4!}+i_1 \frac{\theta^5}{5!}\cdots\\\small
&=& (1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}\cdots)+
i_1(\theta- \frac{\theta^3}{3!}+\frac{\theta^5}{5!}\cdots)\\\small
&=&cos(\theta)+i_1 sin(\theta)
\end{eqnarray}
\]
R2 =r1 2 +r2 2 +r3 2 =1 の条件設定と in 2 =-1の規則により([r1 r2 r3 ].[i1 i2 i3 ])2 =1 となり、偶数項は 係数1のcos展開項となる。また、奇数項はsin展開項として4元数の虚数部が集まる。
ここでr1 、r2 、r3 の制限を外し、θを戻すと以下の三角関数展開形が得られる。
\[\small
\begin{eqnarray}
r&=&\cos{\frac{\theta}{2}}+(r_1 i_1+r_2 i_2+r_3i_3)\sin{{\frac{\theta}{2}}}
\end{eqnarray}
\tt \tag{Eq1.1-8}
\]
このrを使って以下の式により、任意の点 v を左に θ だけ回転させた v~ を得ることが出来る。
\[\small
\tilde{v}=r v r^*
\tt \tag{Eq1.1-9}
\]
r はこの様に回転演算子として働く。
具体例として 以下のようにvをy軸上の座標点 [0 1 0] を指しているものとし、回転軸をx軸方向[1 0 0]に取り、 θ=π/4 だけ回転させてみる。つまり、
\[\small
\begin{eqnarray}
v&=&0 i_1+1 i_2+0 i_3=i_2,\\\small
r&=&\cos{\frac{\pi}{8}}+(1 i_1+0 i_2+0 i_3)\sin{{\frac{\pi}{8}}}\\\small
&=&\cos{\frac{\pi}{8}}+i\sin{{\frac{\pi}{8}}}
\end{eqnarray}
\]
この v と r を使って回転演算を行うと
\[\small
\begin{eqnarray}
rvr^*&=&(\cos{\frac{\pi}{8}}+i_1\sin{{\frac{\pi}{8}}})\space i_2
(\cos{\frac{\pi}{8}}-i_1\sin{{\frac{\pi}{8}}})
\\\small
&=&(i_2\cos{\frac{\pi}{8}}+i_1 i_2\sin{{\frac{\pi}{8}}})
\space(\cos{\frac{\pi}{8}}-i_1\sin{{\frac{\pi}{8}}})
\\\small
&=&i_2(\cos^2{\frac{\pi}{8}}-\sin^2{\frac{\pi}{8}})+2i_3\sin{{\frac{\pi}{8}}}\cos{\frac{\pi}{8}}\\\small
&=&\frac{1}{\sqrt{2}}i_2+\frac{1}{\sqrt{2}}i_3
\end{eqnarray}
\]
y-z 平面上で45度左回転したv~ =[1/√2 1/√2 0] を得ることができた。
この4元数は量子力学や解析力学でおなじみのハミルトニアンを見出した19世紀の数学者・物理学者ハミルトンにより発見された。その後ベクトルや行列の陰にかくれてあまり利用されることが無かったようだ。時を経て現代に回転演算の利便性から有用性が認識され3D ゲームや姿勢制御等に広く応用されているとのこと。
1.2 パウリ行列
4元数の虚数単位と同じ働きをするものに以下のパウリ行列がある。4元数の基底{1, i, j, k} を、{I, σ1 ,σ2 , σ3 }に置き換えたようなものだ。
\[\small
\begin{eqnarray}
\\\small
&& a_0 I+a_1\sigma_1 +a_2\sigma_2 +a_3\sigma_3 ,
\\
\\ \scriptsize
&I&=\begin{bmatrix}1&0\\0&1 \end{bmatrix},\space
\sigma_1=\begin{bmatrix}0&1\\1&0 \end{bmatrix},\\\scriptsize
&\sigma_2&=\begin{bmatrix}0&-i\\i&0 \end{bmatrix},\space
\sigma_3=\begin{bmatrix}1&0\\0&-1 \end{bmatrix}
\end{eqnarray}
\tt \tag{Eq1.2-1}
\]
特に{σ1 ,σ2 , σ3 }はパウリのスピン行列と呼ばれ、これ等の行列の掛算を試してみると以下のように4元数の基底と似通った演算ルールが存在する。
\[\small
\sigma_1. \sigma_1=\sigma_2.\sigma_2=\sigma_3.\sigma_3 =I
\tt \tag{Eq1.2-2}
\]
\[\small
\begin{eqnarray}
&&\sigma_1. \sigma_2=-\sigma_2.\sigma_1=i\sigma_3\\\small
&&\sigma_2. \sigma_3=-\sigma_3.\sigma_2=i\sigma_1\\\small
&&\sigma_3. \sigma_1=-\sigma_1.\sigma_3=i\sigma_2
\end{eqnarray}
\tt \tag{Eq1.2-3}
\]
\[\small
\sigma_1.\sigma_2.\sigma_3 =i I
\tt \tag{Eq1.2-4}
\]
つまり、両者は置き換え可能でありその対応関係は
\[\small
i_k\Leftrightarrow -i\sigma_k,\space 1\Leftrightarrow I
\]
となる。この対応関係を使って以下のように4元数と同じ形式で回転の演算が行う事が出来る。†はrのエルミート転置を意味する。
\[\small
\tilde{v}=r v r^\dagger,\\\small
\begin{eqnarray}
r&=&Exp[-i(a_1\sigma_1+a_2\sigma_2+a_3\sigma_3)\frac{\theta}{2}]\\\small
&=&\cos{\frac{\theta}{2}}I-i(a_1 \sigma_1+a_2\sigma_2+a_3\sigma_3)\sin{{\frac{\theta}{2}}}
\end{eqnarray}
\tt \tag{Eq1.2-5}
\]
上記のように4元数とパウリ行列の対応関係では符号が反転している。rのエルミート転置を取ってvを挟む r と r† の位置を入れ替えて、虚数部の符号を反転させた
\[\small
\tilde{v}=r^\dagger v r,\\\small
\begin{eqnarray}
r&=&Exp[i(a_1\sigma_1+a_2\sigma_2+a_3\sigma_3)\frac{\theta}{2}]\\\small
&=&\cos{\frac{\theta}{2}}I+i(a_1 \sigma_1+a_2\sigma_2+a_3\sigma_3)\sin{{\frac{\theta}{2}}}
\end{eqnarray}
\]
\[\small
\tt \tag{Eq1.2-6}
\]
が座りが良い。演算結果の4元数は以下のように各基底の成分が割り振られている。
\[
\begin{eqnarray}
\\\small
\tilde{v}&=&a_0\sigma_0+a_1\sigma_1+a_2\sigma_2+a_3\sigma_3 \\
&=&\begin{bmatrix}\scriptsize a_0+ a_3&\scriptsize a_1- a_2i\\\scriptsize
a_1+ a_2i&\scriptsize a_0 -a_3 \end{bmatrix}
\end{eqnarray}
\]
\[\small
\tt \tag{Eq1.2-7}
\]
各基底の成分抽出はベクトル空間のそれと同様で、対象基底との内積 v~ n, n=1,2,3 をそれぞれ計算する。
演算規則の σ1 .σ1 =σ2 .σ2 =σ3 .σ3 =I より推察できることだが、基底σn,n=0~3 の成分は v~ n により対角部に集まってくる。したがって、対角成分の総和 Tr(Rv~ n /N)) を計算すれば良い。Nはパウリ行列の成分数で、N=2。
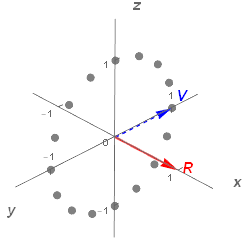
4元数の場合と同じ V=[0 1 0] と R=[1 0 0] を使って回転演算を試してみよう。
下記のグレーの各点は θ を π/8 刻みで回転させた結果のプロットとなる。
Fig1.2-1
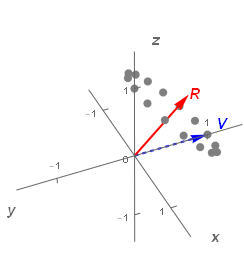
尚、分かりやすくするため直交関係にある V=[0 1 0]、R=[1 0 0] としたが、当然任意の組み合わせでも成り立つ。以下は回転軸を45度傾けたR=[0 1/√2 1/√2]の例となる。
Fig1.2-2
2. スピノル
2.1 回転演算の仕組み
この後示されるディラック方程式では前出の パウリ行列が使われ、シュレディンガー方程式を相対論に適合させるうえで重要な役目をはたした。四元数の行列版と言えるパウリ行列とは何者なのか、回転演算の仕組みの理解を通してもう少し掘り下げてみよう。そのためにはスピノルに関する知識が重要となる。
以下、本節ではhttp://phys.co-suite.jp/note.html に掲載されていた”物理学者のためのスピノル入門”および内部参照下記ペンローズ・リンデラー著を参考文献とした。
Spinors and Space-time R.PENROSE & W.RINDLER
[注意事項]パウリ行列の用途別の整理 本文献においてσ2 の符号が本稿第1章と逆になっている。本稿では第1章と同様パウリ行列は以下のを使用し、
\[\small
\begin{eqnarray}
\sigma&\equiv&[\sigma_0 \space\sigma_1 \space\sigma_2 \space\sigma_3],
\\\scriptsize
\sigma_0&=&\scriptsize\begin{bmatrix}1&0\\0&1 \end{bmatrix},\space
\sigma_1=\begin{bmatrix}0&1\\1&0 \end{bmatrix},\space\sigma_2=\begin{bmatrix}0&-i\\i&0 \end{bmatrix},\space
\sigma_3=\begin{bmatrix}1&0\\0&-1 \end{bmatrix}
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-1a}
\]
σ2 が逆符号の系列に対しては以下の様に 共役を取って表す。
\[\small
\begin{eqnarray}
\sigma^*&\equiv&[\sigma_0^* \space\sigma_1^* \space\sigma_2^* \space\sigma_3^*],
\\\scriptsize
\sigma_0^*&=&\scriptsize\begin{bmatrix}1&0\\0&1 \end{bmatrix},\space
\sigma_1^*=\begin{bmatrix}0&1\\1&0 \end{bmatrix},\space\sigma_2^*=\begin{bmatrix}0&i\\-i&0 \end{bmatrix},\space
\sigma_3^*=\begin{bmatrix}1&0\\0&-1 \end{bmatrix}
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-1b}
\]
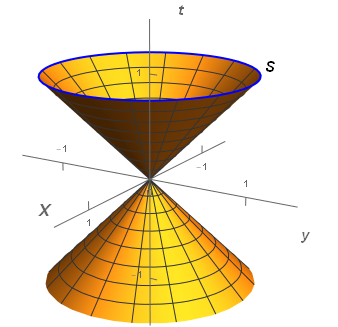
特殊相対性理論の幾何学基盤はミンコフスキー時空だ。時空の特質として、しばしば解説される光円錐を振り返ってみよう。t=0で原点から発せられた光は3次元空間(x, y, z)を時間とともに球面が膨張する様に広がってゆく。図に描けないのでz軸を省いて(t, x, y)で3Dプロットすると以下の様な図となる。図では上面時刻t=1で半径1の円周Sに到達しているが、zを含めた3次元の実際はでは、半径1の球面Sとなる。
Fig2.1-1
この(4次元時空に浮かんだ)球面S上に点Pをとり、デカルト座標P(x,y,z)で表す。次に、このPの属する平面Sを以下のように赤道位置にあるx-y平面に複素平面を重ね、次に球面の北極点から点Pを通る直線を引き、x-y平面との交点を写像点P’とする。
Fig2.1-2
これにより写像点P’を以下の様に複素数 ζ で定義できる。
\[\small
\begin{eqnarray}
\zeta&=&\frac{x}{t-z}+i\frac{y}{t-z}\\\small
\end{eqnarray}
\tt \tag{Eq2.1-2}
\]
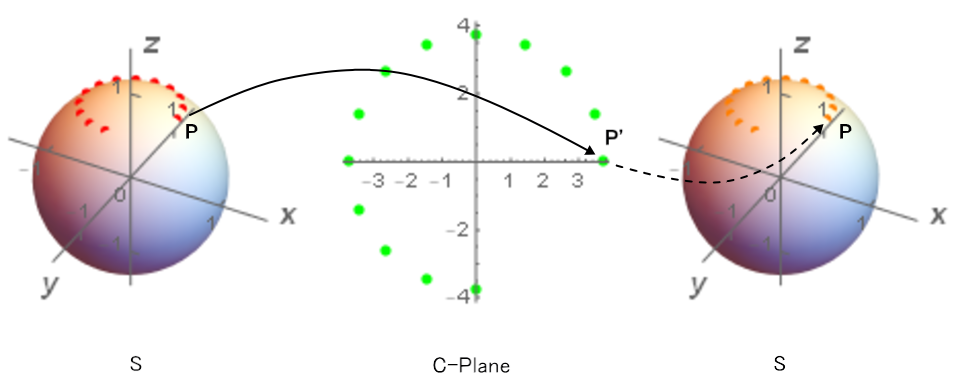
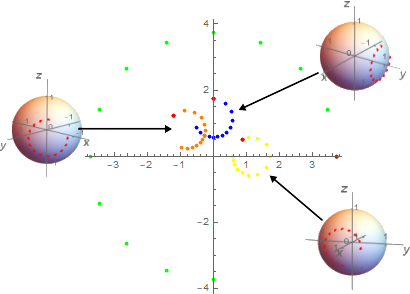
具体的な例を示そう。左の図がSでz 軸周りに赤い点を12個打ってある。真ん中の図が S → ζ への写像であり緑の写像点が12個写像点が原点を中心に円形に並んでいる。
Fig2.1-2
右端のオレンジの点が ζ → S空間への逆写像点となる。逆写像点への変換は
\[\small
\begin{eqnarray}
x&=&\frac{\zeta+\zeta^*}{\zeta \zeta^*+1},\\\small
y&=&\frac{\zeta-\zeta^*}{i(\zeta \zeta^*+1)},\\\small
z&=&\frac{\zeta \zeta^*-1}{\zeta \zeta^*+1}.
\end{eqnarray}
\tt \tag{Eq2.1-3}
\]
となる。実際に以下のζの写像の式 を、上記Eq2.1-3 に入れて確認してみてほしい。尚、本章では回転を扱うのでt=1とする。
\[\small
\begin{eqnarray}
\zeta&=&\frac{x}{t-z}+i\frac{y}{t-z}\\\small
&=&\frac{x+iy}{1-z}.
\end{eqnarray}
\]
北極点は特異点となっているので扱えないが、それ以外は3次元の座標を要する球面上の点を1個の複素数(2次元)で表すことが出来た。Fig2.1-2における緑のz軸回転写像に他の軸回転の様子を重ねてみよう。x軸回転の場合は以下黄色の表示点、y軸回転の場合は青色の表示点、さらにx-y中間の軸による回転の場合はオレンジ色表示点の様に写像される。以下Fig2.1-3を参照。
Fig2.1-3
回転方向や間隔がずれるが、緑のz軸回転と似通った円状の写像が描かれた。複素平面なので何か回転に関するご利益がありそう?
特異点対策として以下の様に ζ=ξ0 /ξ1 の様に新たな複素数の比率で表してみる。ただし|ξ0 |2 +|ξ1 |2 =√2となるように規格化されているものとする。
\[\small
\zeta=\frac{\xi_0}{\xi_1},\\\small
\xi_0 \xi_0^*+\xi_1 \xi_1^*=\sqrt{2}
\tt \tag{Eq2.1-4}
\]
ここでペアとなった(ξ0 , ξ1 )を座標と見なすと、ζ=ξ0 /ξ1 の表現では扱えなかったN点を(√2, 0)の様に表すことが出来る。この様に写像ζを表す規格化されペアで定義された複素数ξ0 , ξ1 がスピノルと呼ばれている様だ。このスピノルのペアを2次元複素ベクトルと見なすと、長さが一定のベクトルなので、4次元空間に浮かぶ3次元超球面を指し示すことになる。
*なぜ√2で規格化するか? このうち “2” という数字はベクトルの成分数が2個あることから来る。この後写像、逆写像の式を確認するが『1に規格化して、どちらかの係数を1にして反対側を2にするか、それとも√2で規格化しておいて両方とも1/√2の係数を使うようにしておくかな?』ぐらいのところだろう。
Eqxx-1に上記を代入すると規格化の条件により、
\[\small
\begin{eqnarray}
x&=&\frac{1}{\sqrt{2}}(\xi_0 \xi_1^*+\xi_0^* \xi_1)
,\\\small
y&=&\frac{1}{\sqrt{2}}(-i \xi_0 \xi_1^*+i \xi_0^* \xi_1),\\\small
z&=&\frac{1}{\sqrt{2}}(\xi_0 \xi_0^*-\xi_1^* \xi_1).
\end{eqnarray}
\tt \tag{Eq2.1-5}
\]
加えて、規格化条件の式自体は
\[\small
\begin{eqnarray}
1&=&\frac{1}{\sqrt{2}}(\xi_0 \xi_0^*+\xi_1^* \xi_1)
\end{eqnarray}
\tt \tag{Eq2.1-6}
\]
以上はさらに以下の通り記述できる。
\[\small
\begin{eqnarray}\small
x&=&\frac{1}{\sqrt{2}}\begin{bmatrix}\xi_0 & \xi_1 \end{bmatrix}\begin{bmatrix}0 & 1 \\1 & 0 \end{bmatrix}\begin{bmatrix}\xi_0^*\\ \xi_1^* \end{bmatrix}\\\small
&=&\frac{1}{\sqrt{2}}\xi \sigma_1 \xi^*
\end{eqnarray}
\]
\[\small
\begin{eqnarray}\small
y&=&\frac{1}{\sqrt{2}}\begin{bmatrix}\xi_0& \xi_1 \end{bmatrix}\begin{bmatrix}0 & -i \\i & 0 \end{bmatrix}\begin{bmatrix}\xi_0^* \\ \xi_1^* \end{bmatrix}\\\small
&=& \frac{1}{\sqrt{2}}\xi \sigma_2\xi^*
\end{eqnarray}
\]
\[\small
\begin{eqnarray}\small
z&=&\frac{1}{\sqrt{2}}\begin{bmatrix}\xi_0 & \xi_1 \end{bmatrix}\begin{bmatrix}1 & 0 \\0 &- 1 \end{bmatrix}\begin{bmatrix}\xi_0^*\\ \xi_1^* \end{bmatrix}\\\small
&=& \frac{1}{\sqrt{2}}\xi \sigma_3 \xi^*
\end{eqnarray}
\]
\[\small
\begin{eqnarray}\small
1&=&\frac{1}{\sqrt{2}}\begin{bmatrix}\xi_0 & \xi_1 \end{bmatrix}\begin{bmatrix}1 & 0 \\0 &1 \end{bmatrix}\begin{bmatrix}\xi_0^*\\ \xi_1^* \end{bmatrix}\\\small
&=& \frac{1}{\sqrt{2}}\xi \sigma_0 \xi^*
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-7}
\]
これはξからSへの逆写像となる。写像空間でこのベクトル Pξ0ξ1 =[ξ0 ξ1 ] に対し、あるいはこれを使って、さまざまな演算を行うがξ0 /ξ1 を直接計算しないようにすればよく、演算が終わったら上記の式でS空間にもどせばよい。
次に本来最初に行うべきSからξへの写像の式を導出しよう。
見通しを良くするために、上記逆写像の4っつの式から規格化係数√2をはずして並べ変えててみる。
\[\small
\begin{eqnarray}
1&=&\xi_0 \xi_0^*+\xi_1 \xi_1^*\\\small
z&=&\xi_0 \xi_0^*-\xi_1 \xi_1^*\\\\\small
x&=&\xi_0 \xi_1^*+ \xi_1\xi_0^*\\\small
y&=&-i \xi_0 \xi_1^*+i \xi_1\xi_0^*
\end{eqnarray}
\tt \tag{Eq2.1-8}
\]
上記の組み合わせを表現するために、
\[\small
\begin{eqnarray}
\xi&\equiv&\begin{bmatrix}\xi_0 \\amp; \xi_1 \end{bmatrix}
\end{eqnarray}
\tt \tag{Eq2.1-9}
\]
とし、自身の共役転置ξ† =[ξ0 * ξ1 *]とのクロネッカー積で展開してみると、以下の様に逆写像の式に必要な全ての係数が得られる。
\[\small
\begin{eqnarray}
\xi\otimes\xi^*=\begin{bmatrix} \xi_0 \xi_0^* & \xi_0 \xi_1^* \\\xi_1 \xi_0^* & \xi_1\xi_1^*\end{bmatrix}
\end{eqnarray}
\tt \tag{Eq2.1-10}
\]
これを分かりやすくするために、対角成分と逆対角成分の二つの基底に分解してみる。
\[\small
\begin{eqnarray}
=\begin{bmatrix}
\xi_0 \xi_0 ^*& 0 \\
0 & \xi_1 \xi_1^*\end{bmatrix}
+\begin{bmatrix}
0 & \xi_0 \xi_1^* \\
\xi_1 \xi_0^* & 0\end{bmatrix}
\end{eqnarray}
\]
対角成分にはt(=1)の写像とzの写像を、逆対角成分にはxとyの写像を重畳できることが分かる。
係数を戻してまとめると以下の写像関係の式を得る。
\[\small
\begin{eqnarray}
&=&\frac{1}{\sqrt{2}}
\left(\begin{bmatrix}
t+z & 0 \\
0 & t-z \end{bmatrix}
+\begin{bmatrix}
0 & x+i y \\
x-i y & 0\end{bmatrix}
\right)
\\&=&\frac{1}{\sqrt{2}}\begin{bmatrix}
t+z & x+i y \\
x-i y & t-z \end{bmatrix}
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-11}
\]
球面 [x y z]からスピノル [ξ0 ξ2 ]への写像
\[\small
P_{xyz} \rightarrow P_{\xi_0 \xi_1}
\]
は以下のスピノルの組み合わせた行列(星取り表?)に対する等式が得られる。
\[\small
\begin{eqnarray}
\xi\otimes\xi^*
&=&\begin{bmatrix} \xi_0 \xi_0^* & \xi_0 \xi_1^* \\\xi_1 \xi_0^* & \xi_1\xi_1^*\end{bmatrix}\\\
&=&\frac{1}{\sqrt{2}}\begin{bmatrix}
t+z & x+i y \\
x-i y & t-z \end{bmatrix}\\\
&=&\frac{1}{\sqrt{2}}\left(
\small t\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}
+x\begin{bmatrix}0 & 1 \\ 1 & 0 \end{bmatrix}
+y\begin{bmatrix}0 & i \\ -i & 0 \end{bmatrix}
+z\begin{bmatrix}1 & 0 \\ 0 & -1 \end{bmatrix}
\right)
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-12}
\]
これから分かる様にスピノルは以下の様にスピン行列(の補数行列)を基底したベクトル空間の住人と言えるのかもしれない。
\[\small
\begin{eqnarray}
\xi\otimes\xi^*=&\frac{1}{\sqrt{2}}(t \sigma_0^*+x\sigma_1^*
+y\sigma_2^*+z\sigma_3^*)
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-13}
\]
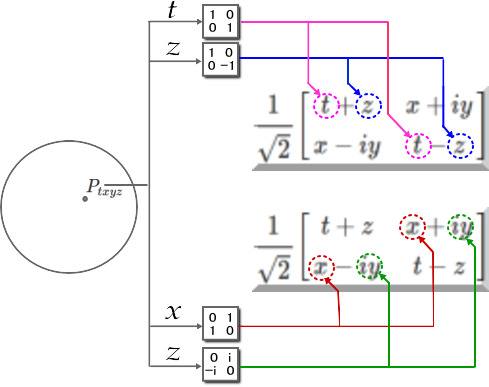
以上の数式を図にすると以下の様になる。
Fig2.1-4
この様に パウリ行列はスピノル行列の要素にどのように配置するかを示す『マッパー』と言える。
逆にスピノル[ξ0 ξ2 ]から球面 [x y z] への変換は以下、前出の通り、パウリ行列をスピノルで挟む演算となる。
\[\small
P’_{\xi_0 \xi_1} \rightarrow P_{xyz}
\]
\[\small
\begin{eqnarray}
x&=&\frac{1}{\sqrt{2}}( \xi_0 \xi_1^*+\xi_1\xi_0^*)=\xi\sigma_1 \xi^*\\\small
y&=&\frac{1}{\sqrt{2}}( -i \xi_0 \xi_1^*+i\xi_0^* \xi_1)=\xi\sigma_2 \xi^*\\\small
z&=&\frac{1}{\sqrt{2}}( \xi_0\xi_0^* – \xi_1 \xi_1^*)=\xi\sigma_3 \xi^*\\\small
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-14}
\]
次に球面上の点Pをz軸回りに回転させてみよう。以下の操作でx-y平面を点Pは回転する。
\[\small
\begin{eqnarray}
\begin{bmatrix}x’\\y’\end{bmatrix}=\begin{bmatrix}\cos{\theta}&-\sin{\theta}\\\sin{\theta}&\cos{\theta}\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}
\end{eqnarray}
\tt \tag{Eq2.1-15}
\]
ところで。この回転操作をスピノル上で行うためにはどうすればよいだろうか?x、yはスピノル基底上では以下の様に逆対角成分にマッピングされている。
\[\small
\begin{eqnarray}
\begin{bmatrix}&x\\x& \end{bmatrix}=x\begin{bmatrix}&1\\1& \end{bmatrix}
\end{eqnarray}
\]
\[\small
\begin{eqnarray}
\begin{bmatrix}&iy\\-iy& \end{bmatrix}=y\begin{bmatrix}&i\\-i& \end{bmatrix}
\end{eqnarray}
\]
つまりx、yはスピノル座標上、以下の様に1点を示すことになる。
\[\small
\begin{eqnarray}
\begin{bmatrix}&x+iy\\x-iy& \end{bmatrix}=x\begin{bmatrix}&1\\1& \end{bmatrix}+y\begin{bmatrix}&
i\\-i& \end{bmatrix}
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-16}
\]
尚、0の成分は空白とした。
この状態でスピノル成分を操作してx、yをθだけ回転した成分に変更したい。分かりやすくxとyを分離して書いたが、要は 以下の様に成分をいじりたい。
\[\small
\begin{eqnarray}
\begin{bmatrix}&x’\\x’& \end{bmatrix}&=&
\begin{bmatrix}&x \cos{\theta}-y\sin{\theta}\\x \cos{\theta}+y\sin{\theta}& \end{bmatrix}\\\\
&+& \\\\\small
\begin{bmatrix}&iy’\\-iy’& \end{bmatrix}&=&
\begin{bmatrix}&i(y\sin{\theta}+x \cos{\theta})\\-i(y\sin{\theta}+x \cos{\theta})& \end{bmatrix}
\end{eqnarray}
\]
写像ζの場合、z軸回転による変換は図xxxより以下の変換となることは簡単に理解できる。
\[\small
\zeta’=e^{i\theta}\zeta
\tt \tag{Eq2.1-17}
\]
スピノル [ξ0 ξ1 ]の場合は ζ =ξ0 (1/ξ1 )の関係により以下の変換が推察できる。
\[\small
\begin{eqnarray}
\begin{bmatrix}\xi’_0\\\xi’_1 \end{bmatrix}=
\begin{bmatrix}e^{i\frac{\theta}{2}}&\\& e^{-i\frac{\theta}{2}}\end{bmatrix}
\begin{bmatrix}\xi_0\\\xi_1 \end{bmatrix}
\end{eqnarray}
\tt \tag{Eq2.1-18}
\]
つまり変換行列をUθ とすると、ξ’=Uθ .ξなのでスピノルξ⊗ξ* の成分を変換しようとする場合、[ξ⊗ ξ* ]↦[ξ’⊗ ξ’* ] =[ (Uθ .ξ)⊗(ξ* .Uθ * )] となり、以下の様に両脇から回転行列で挟むことになる。
\[\small
\begin{eqnarray}&&
\begin{bmatrix}e^{i\frac{\theta}{2}}&\\& e^{-i\frac{\theta}{2}}\end{bmatrix}
\begin{bmatrix}1+z&\color{red}x+i\color{green}y\\\color{red}x-i\color{green}y&1-z \end{bmatrix}
\begin{bmatrix}e^{-i\frac{\theta}{2}}&\\& e^{{i\frac{\theta}{2}}}\end{bmatrix}\\\small
&=&\begin{bmatrix}1+z&e^{i \theta}(\color{red}x+i\color{green}y)\\e^{-i \theta}(\color{red}x-i\color{green}y)&1-z\end{bmatrix}
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-19}
\]
2行目の結果の通り、x-y平面での回転に対応するようにスピノルの成分を変換していることが理解できる。
このz軸回転の例では、変換対象のx-y成分は以下の通り、スピノル行列の逆対角成分に {x,x}+{iy,-iy}={x+iy, x-iy} の形で多重されていたため 単純に eiθ を逆対角成分に掛けるだけですんだ。
\[\small
\begin{eqnarray}&&
\begin{bmatrix}&x-iy\\x+iy&\end{bmatrix}
\end{eqnarray}
\tt \tag{Eq2.1-20}
\]
しかしx軸によるy-z平面や、y軸によるz-x平面の回転の場合は、別々の対角成分にマッピングされている。従ってそれぞれの成分に対して回転の操作を分配する必要がある。
そこでeiθ による回転操作を三角関数による表現に書き換えるてみる。
\[\small
\begin{eqnarray}
\begin{bmatrix}\xi’_0\\\xi’_1 \end{bmatrix}=
\begin{bmatrix}\cos{\frac{\theta}{2}}+i \sin{\frac{\theta}{2}}&\\& \cos{\frac{\theta}{2}}-i \sin{\frac{\theta}{2}}\end{bmatrix}
\begin{bmatrix}\xi_0\\\xi_1 \end{bmatrix}
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-21}
\]
この内、 cos(θ/2) は単位行列(σ0 )に対応し、i sin(θ/2) は回転軸zに対応していることが推察できる。z成分の符号は[+ - ]であることに注目。そこでi sin(θ/2)を切り離し、x軸やy軸に対応する成分位置に移せば良いことが分かる。
尚、回転行列は以下の様に、パウリ行列で記述できる。
\[\small
\begin{eqnarray}
\begin{bmatrix}\cos{\frac{\theta}{2}}+i \sin{\frac{\theta}{2}}&\\& \cos{\frac{\theta}{2}}-i \sin{\frac{\theta}{2}}\end{bmatrix}
=\cos{\frac{\theta}{2}}\sigma_0^*+i \sin{\frac{\theta}{2}}\sigma_3^*
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-22}
\]
x軸に沿ってy-z平面上の点を回転させる場合は、以下成分が操作対象となる。
\[\small
\begin{eqnarray}&&
\begin{bmatrix}\color{blue}z&i\color{green}y\\-i\color{\green}y&-\color{blue}z\end{bmatrix}
\end{eqnarray}
\tt \tag{Eq2.1-23}
\]
z軸の場合に倣ってx軸の符号を考慮(x成分の符号は[+ + ])しながらi sin(θ/2)位置を以下の様に移せば良い。
\[\small
\begin{eqnarray}
\begin{bmatrix}\xi’_0\\\xi’_1 \end{bmatrix}=
\begin{bmatrix}\cos{\frac{\theta}{2}}&i \sin{\frac{\theta}{2}}\\ i \sin{\frac{\theta}{2}}&\cos{\frac{\theta}{2}}\end{bmatrix}
\begin{bmatrix}\xi_0\\\xi_1 \end{bmatrix}
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-24}
\]
z軸の場合と同様に、回転行列は以下の様に、パウリ行列で記述できる。
\[\small
\begin{eqnarray}
\begin{bmatrix}\cos{\frac{\theta}{2}}&i \sin{\frac{\theta}{2}}\\ i \sin{\frac{\theta}{2}}&\cos{\frac{\theta}{2}}\end{bmatrix}
=\cos{\frac{\theta}{2}}\sigma_0^*+i \sin{\frac{\theta}{2}}\sigma_1^*
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-25}
\]
この回転行列でスピノル行列を両方から挟み計算すると、
\[\small
\begin{eqnarray}&&
\begin{bmatrix}\cos{\frac{\theta}{2}}&i \sin{\frac{\theta}{2}}\\ i \sin{\frac{\theta}{2}}&\cos{\frac{\theta}{2}}\end{bmatrix}
\begin{bmatrix}1+\color{blue}z&x+i\color{green}y\\x-i\color{green}y&1-\color{blue}z\end{bmatrix}
\begin{bmatrix}\cos{\frac{\theta}{2}}&-i \sin{\frac{\theta}{2}}\\ -i \sin{\frac{\theta}{2}}&\cos{\frac{\theta}{2}}\end{bmatrix}\\\small
&=&\begin{bmatrix}1+\color{blue}{(z \cos{\theta}+y\sin{\theta})}&x+i\color{green}{(y \cos{\theta}-z\sin{\theta})}\\ x-i\color{green}{(y \cos{\theta}-z\sin{\theta})}&1-\color{blue}{(z \cos{\theta}+y\sin{\theta})}\end{bmatrix}
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-26}
\]
となり、y-z平面の回転となっている。
y軸に沿ってz-x平面上の点を回転させる場合は、以下の成分が操作対象となる。
\[\small
\begin{eqnarray}&&
\begin{bmatrix}\color{blue}z&\color{\red}x\\\color{\red}x&-\color{blue}z\end{bmatrix}
\end{eqnarray}
\tt \tag{Eq2.1-27}
\]
同様に符号を考慮(y成分の符号は[-i +i ])しながら、以下の通り目的の位置に移せば良い。
\[\small
\begin{eqnarray}
\begin{bmatrix}\xi’_0\\\xi’_1 \end{bmatrix}=
\begin{bmatrix}\cos{\frac{\theta}{2}}&-\sin{\frac{\theta}{2}}\\ \sin{\frac{\theta}{2}}&\cos{\frac{\theta}{2}}\end{bmatrix}
\begin{bmatrix}\xi_0\\\xi_1 \end{bmatrix}
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-28}
\]
ここで、回転行列は以下の様に、パウリ行列で記述できる。
\[\small
\begin{eqnarray}
\begin{bmatrix}\cos{\frac{\theta}{2}}&-\sin{\frac{\theta}{2}}\\\sin{\frac{\theta}{2}}&\cos{\frac{\theta}{2}}\end{bmatrix}
=\cos{\frac{\theta}{2}}\sigma_0^*+i \sin{\frac{\theta}{2}}\sigma_2^*
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-29}
\]
結果は、
\[\small
\begin{eqnarray}&&
\begin{bmatrix}\cos{\frac{\theta}{2}}&-\sin{\frac{\theta}{2}}\\ \sin{\frac{\theta}{2}}&\cos{\frac{\theta}{2}}\end{bmatrix}
\begin{bmatrix}1+\color{blue}z&\color{red}x+iy\\\color{red}x-iy&1-\color{blue}z\end{bmatrix}
\begin{bmatrix}\cos{\frac{\theta}{2}}&\sin{\frac{\theta}{2}}\\ – \sin{\frac{\theta}{2}}&\cos{\frac{\theta}{2}}\end{bmatrix}\\\small
&=&\begin{bmatrix}1+\color{blue}{(z \cos{\theta}-x\sin{\theta})}&\color{red}{(x \cos{\theta}+z\sin{\theta})}+iy\\ \color{red}{(x\cos{\theta}+z\sin{\theta})}-iy&1-\color{blue}{(z \cos{\theta}-x\sin{\theta})}\end{bmatrix}
\end{eqnarray}
\]
\[\small
\tt \tag{Eq2.1-30}
\]
となり、z-x平面での回転となっている。
任意の回転軸 rxyz =[rx ry rz ]に対して上記のx軸、y軸、z軸の個別回転を線形加算したRξ0ξ1 (θ)がスピノルへの回転演算子となり、
\[\small
R_{\xi_0\xi_1}(\theta)=\cos{\frac{\theta}{2}}\sigma_0^*+i\sin{\frac{\theta}{2}} (r_x\sigma_1^*+r_y\sigma_2^*+r_z\sigma_3^*),\\\small
r_x^2+r_y^2+r_z^2=1.
\]
\[\small
\tt \tag{Eq2.1-31}
\]
以下の線形変換でスピノルを回転させることができる。
\[\small
\tilde{P}_{\xi_0\xi_1}=R_{\xi_0\xi_1}(\theta)\cdot P_{\xi_0\xi_1}\cdot R_{\xi_0\xi_1}^*(\theta)
\tt \tag{Eq2.1-32}
\]
尚、S平面上の点Ptxyz =[1 x y z]からスピノル空間上の点Pξ0ξ1 への写像は以下の式で得られる。
\[\small
P_{\xi_0\xi_1}=\frac{1}{\sqrt{2}}\sigma^*\cdot P_{txyz},\\\small
\sigma^*=[\sigma^*_0 \space \sigma^*_1\space \sigma^*_2\space\sigma^*_3 ].
\tt \tag{Eq2.1-33}
\]
逆にスピノル空間からS平面への逆写像は
\[\small
P_{txyz}=\frac{1}{\sqrt{2}}Tr(\sigma^*\cdot P_{\xi_0\xi_1})
\tt \tag{Eq2.1-34}
\]
あるいは
\[\small
P_{txyz}=\frac{1}{\sqrt{2}} \xi .\sigma.\xi^*
\tt \tag{Eq2.1-35}
\]
2.2 スピノルによるローレンツ変換
ローレンツ変換の式をあらためて書く。以下はローレンツ逆変換の式でz軸に沿ったブーストとなる。
\[\small
\begin{bmatrix}
t’\\\\ \small
z’
\end{bmatrix}=
\begin{bmatrix}
\frac{1}{\sqrt{1-\beta^2}} & \frac{ \space \beta}{\sqrt{1-\beta ^2}} \\
\frac{\space \beta}{\sqrt{1-\beta^2}} & \frac{1}{\sqrt{1-\beta^2}}
\end{bmatrix}
\begin{bmatrix}
\space\space t\\ \\ \small
\space z
\end{bmatrix}
\tt \tag{Eq2.2-1}
\]
\[\small
\tt \tag{Eq2.2-1}
\]
対角成分を共有するtとzの組み合わせに注目し、以下の様に変形してみる。
\[\small
\begin{bmatrix}
t’+z’\\ \small
t’-z’
\end{bmatrix}=
\begin{bmatrix}
w &0 \\
0& w^{-1}
\end{bmatrix}
\begin{bmatrix}
\space\space t+z\\ \small
\space t-z
\end{bmatrix},\\\small
w=\sqrt{ \frac{1+\beta}{1-\beta}}
\tt \tag{Eq2.2-2}
\]
この式を使って回転と同様にスピノル空間[ξ0 ,ξ1 ]でローレンツ変換を行いミンコフスキー時空に戻せることを確認したい。そこで変換後のスピノルは以下であるので、
\[\small
\begin{eqnarray}\tilde{P}_{\xi_0\xi_1}&=&
\tilde{\xi }\otimes\tilde{\xi^* }\\\small&=&\begin{bmatrix}\tilde{\xi }_0\\ \small\tilde{\xi }_1\end{bmatrix}
\begin{bmatrix}\tilde{\xi }^*_0 &\tilde{\xi }^*_1\end{bmatrix}\\\small
&=&\begin{bmatrix}
\tilde{\xi }_0 \tilde{\xi }^*_0 &\tilde{\xi }_0 \tilde{\xi }^*_1 \\\small
\tilde{\xi }_1 \tilde{\xi }^*_0 &\tilde{\xi }_1 \tilde{\xi }^*_1
\end{bmatrix}
\end{eqnarray}
\tt \tag{Eq2.2-3}
\]
これを得るためには下記の様にwを分配すればよいことが分かる。
\[\small
=
\begin{bmatrix}
w^{\frac{1}{2}} &0 \\
0& w^{-\frac{1}{2}}
\end{bmatrix}
\begin{bmatrix}\xi_0\\ \small\xi_1\end{bmatrix}
\begin{bmatrix}\xi^*_0 & \small\xi^*_1\end{bmatrix}
\begin{bmatrix}
w^{\frac{1}{2}} &0 \\
0& w^{-\frac{1}{2}}
\end{bmatrix}
\]
\[\small
\tt \tag{Eq2.2-4}
\]
従ってスピノル座標におけるローレンツ変換は以下の式で表すことが出来る。尚スピノル行列は以下の様に “1”→”t” と変更されている。スピノル自身は2次元複素ベクトルであるから、4次元実数空間と写像関係となりうる。(実数空間での回転を扱う場合は t=1 として次元を隠していたと思えばばよい)
\[\small
\tilde{P}_{\xi_0\xi_1}=
\frac{1}{\sqrt{2}}
\begin{bmatrix}
w^{\frac{1}{2}} &0 \\
0& w^{-\frac{1}{2}}
\end{bmatrix}
\begin{bmatrix}
t+z & x+i y \\
x-i y & t-z \end{bmatrix}
\begin{bmatrix}
w^{\frac{1}{2}} &0 \\
0& w^{-\frac{1}{2}}
\end{bmatrix}
\]
\[\small
\tt \tag{Eq2.2-5}
\]
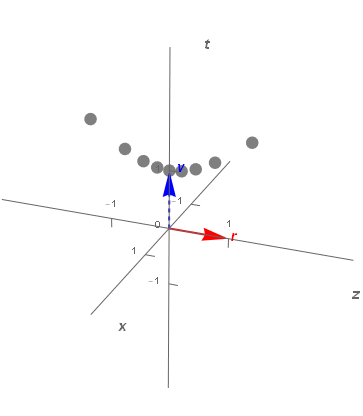
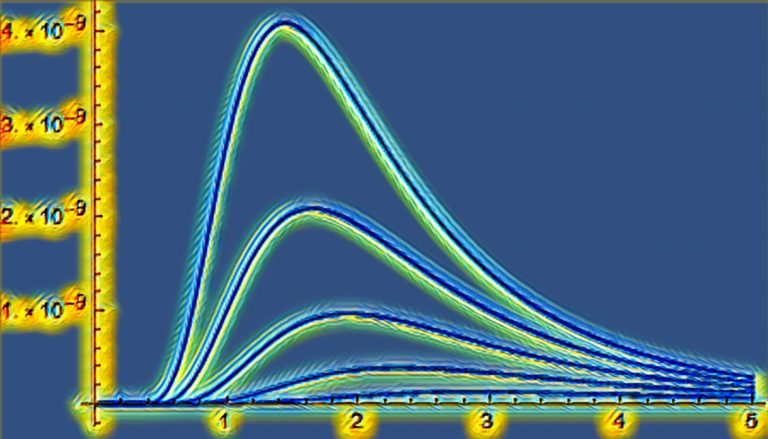
以下、P=(1,0,0,0)、つまりz=0、t=1の時空点をz軸方向に光速度比βを-0.8から0.8まで0.2ずつ振った場合のP’(ローレンツ変換後の移動先)をプロットしたものとなる。
t-z平面に双曲線が描かれ、3番目のβ=+0.6の点で理論通りのt=1.25, z=0.75が確認できる。
回転変換とローレンツ変換の類似性を実感できる別の導出方法も確認しておこう。
ローレンツ変換の元の式で以下の様にβをtanh(θ)に置き換える。
\[\small
\begin{bmatrix}
\frac{t-x \space \beta}{\sqrt{1-\beta^2}}\\ \small
\frac{x-t \space \beta}{\sqrt{1-\beta^2}}
\end{bmatrix}=
\begin{bmatrix}
\frac{1}{\sqrt{1-\tanh{\theta}^2}} & -\frac{ \space \tanh{\theta}}{\sqrt{1-\tanh{\theta} ^2}} \\
-\frac{\space \tanh{\theta}}{\sqrt{1-\tanh{\theta}^2}} & \frac{1}{\sqrt{1-\tanh{\theta}^2}}
\end{bmatrix}
\begin{bmatrix}
\space\space t\\ \\ \small
\space x
\end{bmatrix}
\]
\[\small
\tt \tag{Eq2.2-6}
\]
θ=arctanh(β)となることに注意。
さらにtanh(θ)の項を三角関数の公式に従ってsinh(θ)、cosh(θ)に置き換える。
\[\small
\begin{bmatrix}
\frac{t-x \space \beta}{\sqrt{1-\beta^2}}\\ \small
\frac{x-t \space \beta}{\sqrt{1-\beta^2}}
\end{bmatrix}=
\begin{bmatrix}
\cosh{\theta} & -\sinh{\theta} \\
-\sinh{\theta} & \cosh{\theta}
\end{bmatrix}
\begin{bmatrix}
t\\ \small
x
\end{bmatrix}
\]
\[\small
\tt \tag{Eq2.2-7}
\]
この変換行列は下記の通り、x軸回りの回転行列の実数角θにiを加え虚数角に書き換えたものに等しい。
\[\small
\begin{bmatrix}\cos{i\theta}&i \sin{i\theta}\\ i \sin{i\theta}&\cos{i\theta}\end{bmatrix}
\tt \tag{Eq2.2-8}
\]
従ってスピノル経由でのx軸ブーストによる変換は、x軸回転の回転行列をそのまま使用し、θ➝(iθ)、逆変換ではθ➝(-iθ)と置き換え、r.v.r(r.v.r*ではなく)を計算すれば良い。
x軸の場合
\[\small
\begin{bmatrix}\cos{i\frac{\theta}{2}}&i \sin{i\frac{\theta}{2}}\\ i \sin{i\frac{\theta}{2}}&\cos{i\frac{\theta}{2}}\end{bmatrix}
\tt \tag{Eq2.2-9}
\]
ブースト軸と回転軸rは同じパウリ行列が対応し線形加算がきくので任意の方向へのローレンツ変換が可能となる。
y軸の場合
\[\small
\begin{bmatrix}\cos{i\frac{\theta}{2}}&-\sin{i\frac{\theta}{2}}\\ \sin{i\frac{\theta}{2}}&\cos{i\frac{\theta}{2}}\end{bmatrix}
\tt \tag{Eq2.2-10}
\]
z軸の場合
\[\small
\begin{bmatrix}\cos{i\frac{\theta}{2}}+i \sin{i\frac{\theta}{2}}&0\\0& \cos{i\frac{\theta}{2}}-i \sin{i\frac{\theta}{2}}\end{bmatrix}
\tt \tag{Eq2.2-10}
\]
尚、これは前出の以下のz軸ブースト行列と等価だ。
\[\small
\begin{bmatrix}
w^{\frac{1}{2}} &0 \\
0& w^{-\frac{1}{2}}
\end{bmatrix}
\]
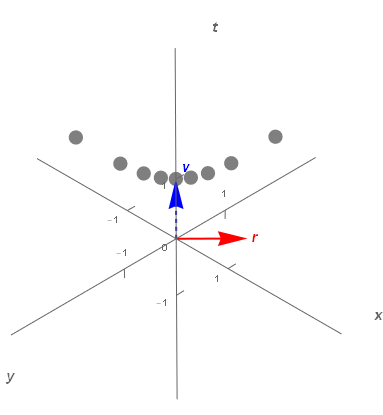
例としてこれ等の行列のうち、x軸、y軸を使った、t-x-y時空でローレンツ変換を確認してみよう。以下はr=(1/√2, 1/√2, 0)の場合となる。これに対応するスピノル行列はt=1, x=0, y=0, z=0と置いてプロットしたものだ。θ=arctanh(β)として光速度比βを-0.8から0.8まで0.2ずつ振ってある。
意図した通りx軸とy軸の中間方向にローレンツ変換された結果が得られている。
3. ディラック方程式
3.1 質量無し(m=0)での解
シュレディンガー方程式におけるエネルギーはE=p2 /(2m0 )というニュートン力学の定義を前提としていた。しかし正しいエネルギーの定義は下記、特殊相対性理論3 力学編のエネルギー・運動量関係式 におけるEq3.3-14である必要がある。
\[\small
E^2=(cp^1)^2+m_0^2 c^4
\]
この式は、元々以下の様に4元運動量ベクトルを示す式からの変形であり、時間成分(p0 側)がエネルギー、空間成分(p1~3 側)が運動量対応している。
\[\small
(cp^0)^2-(cp^1)^2=m_0^2 c^4\\
\downarrow\\\small
E^2-(cp^1)^2=m_0^2 c^4
\]
つまりエネルギーと運動量は対等(運動方程式では同じ形で扱われるはず)であり、m0 2 c4 を不変量としてローレンツ変換される。
以降、数式の変形において定数のcやhがうっとうしいので、 以下の式の様に自然単位系としてc=1、ℏ=1とし、pやmの添え字も省略すると、
\[\small
E^2=p^2+m^2
\tt \tag{Eq3.1-1}
\]
従って量子論でもエネルギーは以下の定義を採用すべきだ。
\[\small
E=\sqrt{p^2+m^2 }
\tt \tag{Eq3.1-2}
\]
波動関数をψ(x,t)と表すとし、Eq2.2-3 の演算子に書き換えると、Eq1.2-1より
\[\small
\begin{eqnarray}
i\partial_t\psi(x,t)
&=&E(\hat{p},x)\psi(x,t)\\\small
&=&\sqrt{-\partial_x^2+m^2 }\psi(x,t)
\end{eqnarray}
\tt \tag{Eq3.1-3}
\]
となる。つまり演算子部分を抜き出して書くと
\[\small
i\partial_t=\sqrt{-\partial_x^2+m^2}
\tt \tag{Eq3.1-4}
\]
と言う関係となる。
前述の通り、そもそも相対性理論における力学では、世界線(運動軌跡)や物理量は固有時間τをパラメータとして時間、空間の成分が線形に混ざり合って4元ベクトルをなしている。従って左辺Eが時間による1階微分で、右辺側Pは(後から√を取るとはいえ)空間による2階微分となることは相対性理論的には筋が悪い。演算の対称性を保つためには√を取る前で対称性のあるEq1.3-1 を検討の出発点とするべきだ。
そこでディラックは行列の式に[?]に置き換えて、かつそののち1階の微分演算子どうししか含まない式に変形できる何かを探ることとした。
\[\small
E^2=[p^2+m^2]\leftrightarrow [\space ? \space]^2
\tt \tag{Eq3.1-5}
\]
まずは簡単な質量の無い、つまりm=0の光子の場合を考えた場合に、
\[\small \begin{eqnarray}
E^2&=&p^2=(p\cdot[\sigma_1 \space \sigma_2 \space \sigma_3])^2\\\small
&=&(p_1\sigma_1+p_2\sigma_2+p_3\sigma_3)^2, \end{eqnarray}\\
\\\scriptsize
\sigma_1=\begin{bmatrix}0&1\\1&0 \end{bmatrix},\space
\sigma_2=\begin{bmatrix}0&-i\\i&0 \end{bmatrix},\space
\sigma_3=\begin{bmatrix}1&0\\0&-1 \end{bmatrix}
\]
\[\small
\tt \tag{Eq3.1-6}
\]
のようなパウリのスピン行列で定義されたへんてこな量を導き出した。もしこれが成り立てば、確かに左右ともに2乗をはずすことが出来、両方とも1階微分とすることができる。
検算してみよう。2乗項を全部展開すると、
\[\small
(p_1\sigma_1+p_2\sigma_2+p_3\sigma_3)^2\\\small
=p_1^2\sigma_1^2+p_2^2\sigma_2^2+p_3^2\sigma_3^2\\\small
+p_1 p_2 \sigma_1 \sigma_2+p_1 p_3 \sigma_1 \sigma_3\\\small
+p_2 p_1 \sigma_2 \sigma_1+p_2 p_3 \sigma_2 \sigma_3\\\small
+p_3 p_1 \sigma_3 \sigma_1+p_3 p_2 \sigma_3 \sigma_2
\\\small
\]
\[\small
\tt \tag{Eq3.1-7}
\]
これに、以下のパウリのスピン行列の特性
\[\small
\sigma_1^2=\sigma_2^2=\sigma_3^2=I\\\small
\]
および、
\[\small
\sigma_1 \sigma_2+\sigma_2 \sigma_1=0,\\\small
\sigma_1 \sigma_3+\sigma_3 \sigma_1=0,\\\small
\sigma_2 \sigma_3+\sigma_3 \sigma_2=0\\\small
\]
を適用すると
\[\small
\begin{eqnarray}
&(&p_1\sigma_1+p_2\sigma_2+p_3\sigma_3)^2\\\small
&=&p_1^2 I+p_2 ^2 I+p_3^2 I \\\small
&=&p_1^2 +p_2 ^2 +p_3^2 = p^2
\end{eqnarray}
\tt \tag{Eq3.1-8}
\]
これにより、以下の様に右辺、左辺ともに自乗の形のまとめられ、Eを1階運動量演算子で求めることが可能となった。
\[\small
E^2=p^2 \quad\rightarrow E=\pm p\cdot[\sigma_1 \space \sigma_2 \space \sigma_3]
\]
\[\small
i\partial_t\psi(p, t)=\pm p\cdot[\sigma_1 \space \sigma_2 \space \sigma_3]\psi(p, t)
\tt \tag{Eq3.1-9}
\]
そしてこの式は前述のEq3.1-5と整合する。
3.2 質量あり(m>0)での解
質量のある場合、つまりm>0の量子のを考えた場合は、
\[\small
\begin{eqnarray}
E^2&=&p^2+m^2=(p\cdot \alpha+\beta m)^2\\\small
&=&(p\cdot[\alpha_1 \space \alpha_2 \space \alpha_3]+\beta m)^2\\\small
\end{eqnarray}
\tt \tag{Eq3.2-1}
\]
とする。ここでI→σ0 と置き換え、α 、β を以下の通り置くと
\[\small
\begin{eqnarray}
\alpha_1&=&-\sigma_1 \otimes \sigma_3\\\small
\alpha_2&=&-\sigma_2 \otimes \sigma_3\\\small
\alpha_1&=&-\sigma_3 \otimes \sigma_3\\\small
\beta\space\space &=& + \sigma_0 \otimes \sigma_1
\end{eqnarray}
\tt \tag{Eq3.2-3}
\]
とするとEq3.2-1が成り立つことが分かる。これは以下の様に2乗を取り払った(つまり確率保存が期待できる1階微分どうしの)等式が得られたことになる。
\[\small
i\partial_t\psi(p, t)=\begin{bmatrix}m& p_x& p_y& p_z\end{bmatrix}\begin{bmatrix} \beta\\ \alpha_1\\ \alpha_2 \\ \alpha_3\end{bmatrix}\psi(p, t)
\tt \tag{Eq3.2-2}
\]
この様にEq3.2-1が成り立つパウリ行列の入れ子的な組み合わせはいくつか存在し、この組み合わせをワイル表示という。
<<執筆中>>
Post Views: 4






コメント