| �O�̃y�[�W | English Here �@�@�ڎ��@�@�@ | ���̃y�[�W |
| Copyright Maeda Yutaka�@�@ |
�@�@�@�@�@�@�@�@�j���[�X�I�@�{�g�o�@�H�Ɛ��w���H�w�Ђ��o�ł���܂����B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@  �Q�D���`�V�X�e�� �Q�D�P�@��ݍ��ݐϕ�(Convolution) �@��ݍ��ݐϕ��� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �ƒ�`����Ă��܂��B��������イ��������̂ł����A���̎��̒����I�ȈӖ����������Â炭�v���܂��B ���Ƃ����������č�������́i���j�̊��ł��B�@�i�сj�͉��̖�ڂ��L��̂ł��傤���H�@��̓I�ȗ����ɁA���������@�艺���ĈӖ����l���Ă݂܂��傤�B �@���`�V�X�e���iRLC��H���j�ւ̓��͂Ƃ��ĒP�ʃC���p���X�����l���܂��B���i���j�͂��̉������Ƃ��܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@ 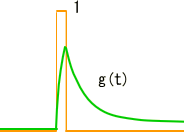 ���̗��RC��H�̂����Ƃ��|�s�����[�ȉ����̗�ŁA���͎w�����ƂȂ�܂��B ���̓C���p���X�Ƃ��̊Ԃɂ͐��`�W������A�C���p���X�����{�����g�����{����܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@ 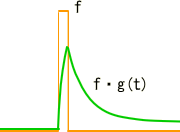 �@�@�@ �@�@�@�����ŁA���̓C���p���X�̑傫�������A���Ԏ���̈ʒu�ɂ���ĕς���Ă�����̂Ƃ��܂��傤�B ���̏ꍇ�ȉ��̗l�ɁA���Ԏ���̃C���p���X�ʒu���тƂ���ƁA���i�сj�Ɗ��̌`�ŕ\���ł��܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@ 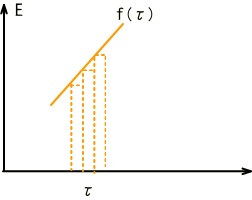 ����A���������̔C�ӂ̎������ɂ�����d���́A�}�̂Ƃ��肇�i��-�сj�ƂȂ�܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@ 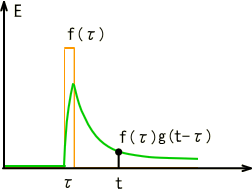 ���āA�ȉ��̐}�̓C���p���X��3�A�����ē��͂��ꂽ�ꍇ�ł��B���̉����́A���ꂼ��̉����̍��v�l�A�܂肻�ꂼ��̉������d�ˍ��킹�����ʂƂȂ�܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@ 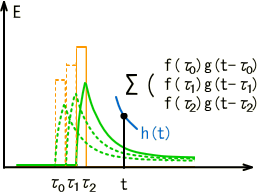 �����ŁA���͐M���̔g�`���C���p���X�̘A���̂ƍl���A���ɂ�鍇�v��ϕ��ɒu��������ƁA �@�@�@�@�@�@�@�@�@�@�@�@�@ �Ƃ����A��قǂ̏�ݍ��ݐϕ��̎����o���オ��܂����B �@�����ōŏ��̋^��A�w�т͉��̖�ڂ�����̂��H�x�ł����A���̗�̏ꍇ�́w���͔g�`�̌`����X�L�������邽�߂̎��Ԏ���̃p�����[�^�[�x�ƌ������ƂɂȂ�܂��B �����Ă��i���j�́A���̓��͔g�`�ɑ��鉞���g�`��\���Ă��܂��B �@��ʂɏ�ݍ��ݐϕ��̉��Z�q���ȉ��̗l�ɃA�X�^���X�N�f���f�ŕ\���܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �܂��A�����͏ȗ����܂����A�ȉ������藧���܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@ �@�Ƃ���ł��̗�ł�������̗l�ɁA��ݍ��݂��o����̂́A�d�ˍ��킹���o����A�܂�w���`���x�ƁA���Ԃ����̂܂܃V�t�g�ł���A�܂�w���s�ϐ��x�ɂ����̂ŁA���`���s�σV�X�e���̓����ƌ����܂��B �t�ɐ��`���s�σV�X�e���ł͒P�ʃC���p����������������A�ǂ�ȓ��͂ɑ��鉞�����A��ݍ��ݐϕ��ɂ�苁�߂���ƌ������ł��B ���A���U�M���ɂ����Ă���ݍ��ݘa�����l�̉��Z�ƂȂ�܂��B �t�[���G�ϊ��iFT�j�ł͊��̏�ݍ��ݐϕ��́A�ϊ��ɂ����̐ςƂȂ�܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@FT �@�@�@�@�@�@�@�@�@�@�@�@�@f(t)*g(t)�@�@�����@�@F(�ցjG�i�ցj �ϊ��͑𐬂��Ă���̂ŁA�ȉ��̂悤�ɋt�����藧���܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@FT �@�@�@�@�@�@�@�@�@�@�@�@�@f(t)g(t)�@�@�@�����@�@F(�ցj*G�i�ցj ����́A�����ŏЉ�����̑��̕ϊ��i���U�t�[���G�ϊ��A���v���X�ϊ����j�ł����l�ɐ��藧���ՓI�ŁA���ɏd�v�Ȍ����Ƃ����܂��B �Q�D�Q�@����ϊ��ƌŗL�l��� �@�ŗL�l���Ƃ͕����A�H�w���̗l�X�ȕ���ŋ��ʂɑ�������ۑ�p�^�[���̈�ł���ƌ����Ă��܂��B�ŗL�l��͂Ƃ́A���̏ꍇ�ɗ��p������@�ł���A���p�͈͂̍L�����ՓI�ȋZ�@�ƌ����܂��B ���ア�낢��ȏ�ʂŕK�v�ƂȂ鎖���\�z����邽�߁A����ϊ��ɂ����鎖����l�@���Ă����܂��B �@DCT��DFT�Ȃǂ̒���ϊ����l���܂��B���`�ϊ��̎��Ƃ��Ĉȉ��̗l�Ɍ�����܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �ϊ��s��a�ɂ��A���̎��ԃx�N�g�����炙�̎��g���x�N�g���ɕϊ�����܂����B ����Ɉȉ��̗l�ɂ��̊e�v�f�ɑ��X�J���[�̌W����ɂ��|���đ傫����ς��Ă݂܂��B���̗l�ɑΊp����ȊO���O�ł���s���Ίp�s��iDiagonal matrix)�ƌĂт܂��B �@�@�@�@�@�@�@�@ 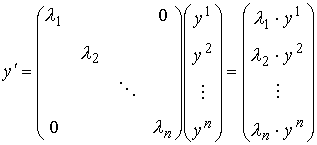 �s��̎��ł́A�ȉ��̗l�ɂȂ�܂��B �@�@�@�@�@�@�@�@�@ 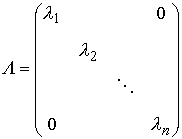 ���g���̈�Ŋe�v�f�̑傫����ς��鎖�́A�t�B���^�[�̑���ƌ����܂��B�g�߂ȂƂ���ł̓X�e���I�Z�b�g�ɕt���Ă���O���t�B�b�N�E�C�R���C�U�[�A���v�̃X���C�h�{�����[���𑀍삷��l�Ȃ��̂ł��傤���B ���̂��f���t�ϊ��ɂ�茳�̎��ԗ̈�ɖ߂��Ă݂܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ���R�A���ԗ̈�ɖ߂��ꂽ�ƌ����Ă��A���f�͌��̂��Ƃ͈قȂ��Ă��܂��܂��B ���̎��͐V���ȕϊ��s��W���`���邱�Ƃɂ��A�ȉ��̗l�Ȑ��`�ϊ��̎��ɐ����ł��܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@ ����W���C�R���C�U�[�A���v�ɑ������A�������͂��ꂽ����ό`���Ă��f�ɏo�͂���Ƃ����C���[�W�ɂȂ�܂��B �@�ł͖��ł��B�w����W�����m�ł������ꍇ�A���Ƃ��f����W�𐄒肵�A����ɂ��ꂪ�ϊ��s��a�ƃt�B���^�[�ɂ��\������Ă���Ƃ���������m�鎖���o����̂ł��傤���H�x�@ ���ꂪ������ŗL�l��͂̈��ł��BScilab���g���Ċm�F���Ă݂܂��傤�B �@DCT�Ŏ��g���̈�ɕϊ���A�t�B���^�����O������ŁA�ēxIDCT�ɂ�莞�ԗ̈�ɖ߂��܂��B �@�@�@�@�@�@�@�@�@�\�[�X�v���O�����@�@�@SciLab_src_EVAL1 �t�B���^�[�����i�ɂ�S�ĂP�j�̏�Ԃł́A�C���p���X���ɑ��鉞���o�͂����ł��B  �@�@�@�@�@�@�@�@�@�@ 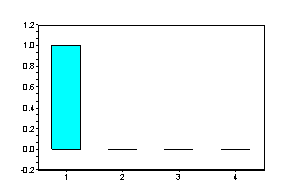 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����o�́F���� ���͂Ɠ����C���p���X���Č�����Ă܂��B �t�B���^�[�ɒ��ʉߌ^�̌W����ݒ肵�Ă݂܂��B 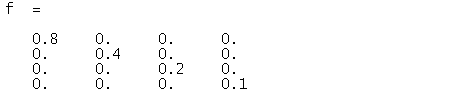 �@�@�@�@�@�@�@�@�@�@ 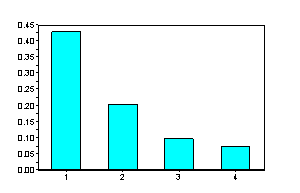 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����o�́F���� �w�����I�ȉ����������܂����B�t�B���^�[�̌��ʂł��B���̏ꍇ�̕ϊ��s�ł��B  ���G�Ȑ���������ł��܂��B�������悭����Əc���Ώ̂ɂȂ��Ă��܂��B�Ώ̍s�邢�̓G���~�[�g�s��ł��邱�Ƃ���������܂��B ���ۂɂ͂��̕ϊ��s��͖��m�ł���A�������ɂ�萄�肷�鎖�ɂȂ�܂��B���̓C���p���X�̈ʒu�������炵�Ȃ���A�Ή������߂čs�����ɂ�苁�߂��܂��B ���A���m��W�������ŋ��܂������̂Ƃ��܂��B���̃f�[�^���t�B���^�[�̌W���ɂ����߂Č��܂��傤�B���̌W���͌ŗL�l�Ƃ��ċ��߂��܂��BScilab�ł͌ŗL�l��spec(W)�Ōv�Z�ł��܂��B�ȉ������̌��ʂł��B  �����͕ʂɂ��āA�����ƃt�B���^�[�̌W�������߂��܂����B �@�ǂ����������Ńt�B���^�[�̌W�����ŗL�l�Ȃ���̂ɑ�������̂����ׂĂ݂܂��傤�B �ϊ��s��͌��X�ȉ��̒ʂ�A�t�B���^�[�W���ɂ��Ίp�s���s��a�ƁA���̋t�s��Ƃŋ����̂ł����B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ���̎��̗��ӂ�a�̋t�s����E���炩���ĕό`���܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ����Aa�͒����s��ł������̂ŋt�s��͓]�u�s��ɒu�������邱�Ƃ��o���܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �����ŁA�ϊ��s��a���ȉ��̗l�ɍs�x�N�g������\������Ă���ƍl���܂��B �@�@�@ 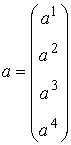 �@,�@������ �@,�@��������������� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �ɂ͂�����ŗL�l�ł���Aai�͂��̌ŗL�l�ɑΉ�����ŗL�x�N�g���ł��B
�ȏ�̎��́A�K�ȃx�N�g����I�Ԃ��Ƃɂ���āA�s��W���ŗL�l�Ƃ����X�J���[�ʂɕϊ��ł��鎖�������Ă��܂��B�����āA���̗l�ȊW�������邱�Ƃ��ŗL�l���ƌ����܂��B�ȉ��̎��͗ʎq�͊w�ɂ�����L���ȃV�����f�B���K�[�̔g���������ł��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ���̎����ŗL�l���ƂȂ��Ă��܂��B�ϑ���H�ɑ��A���͌ŗL�x�N�g���ɑ�������g�����AE�͌ŗL�l�ł���G�l���M�[��\���܂��B�܂肱��������Ǝ��g���X�y�N�g�������܂邱�Ƃ̂Ȃ�܂��B �@����̗�ł͌ŗL�l�̓t�B���^�[�̌W���ł����B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �����ČŗL�x�N�g����DCT�ϊ��̍s�x�N�g���ɑΉ����܂��B���炩�̕��@�ōs��W���ϑ��o�����ꍇ�ɁA�����ϊ��s��ƑΊp�s��i���̗�ł̓t�B���^�[�̌W���j�ɕ������邱�Ƃ́A�H�w�I�ɂ��L�p�Ȏ�@�ł��B���̗l�ȋZ�@��Ίp���ƌ����܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ���m�̍s��v���ŗL�l�A�ŗL�x�N�g�������߂���@�͐��`�㐔�̋��ȏ����Q�l�ɂ��Ă��������B �����I�Ƀt�[���G�ϊ����̒��s�s��Ƌt�s��ŃX�J���[����������s��̌ŗL�l�̓X�J���[��Ɠ������A�����I�ɂ̓t�B���^�[�ł��B�܂��ŗL�x�N�g���͋��Ƃ��̒��s�s��ł��B�i��ʓI�ɏ��Ԃ͍Č�����܂��j �����ŏЉ���t�B���^�[�i�ŗL�l�j�́A���̌������郉�v���X�ϊ��ŏd�v�Ȗ������͂������� �ƂȂ�܂��B 2�D3�@���v���X�ϊ��E���ϊ� ���v���X�ϊ� �@�t�[���G�ϊ��ł͋����������g���������W�����Ƃ��ė��p���Ă���Ƃ����C���[�W�ł��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ 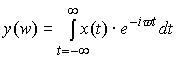 �Ȃ��Ȃ�e-i��t��t���p�����[�^�Ƃ��ĕ��f���ʂ��N���N���Ɖ�]�����킯�ł���A�ւ͂��̉�]���x�W���ƂȂ�܂��B��������̉�]���x�W���ւ̈ʒu�ƁA�g�`��Δ䂳���Ă݂�ƈȉ��̐}�̗l�ɂȂ�܂��B�@ �@�@�@�@�@�@�@�@�@ 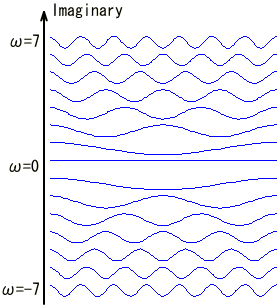 �@�@�@�@�@�@�@ �@�@�@�@�@�@�@����e��t�@�̗l�Ɏw�����������̏ꍇ���l���Ă݂܂��B�����O�ł͓��R�I�[���P�̒����ł��B��������Ƀ����O�ł͂P����O�Ɏ������܂��B�����O�ł͂P���甭�U���Ă��܂��B �@�@�@�@�@�@�@�@�@ 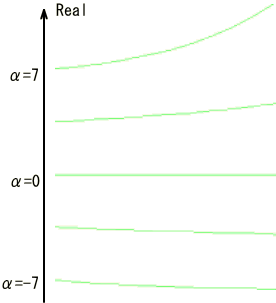 �@���v���X�ϊ��͂���2�̎�����g�ݍ��킹�Đ��^�V�X�e���̉ߓn�������͂��悤�ƌ��������ł��傤���B �ϊ����͈ȉ��̗l�Ƀt�[���G�ϊ��̉�]���q�ɐU���̔��U�E������\�������ɂ��w������e-��t���|�����Ă��܂��B �@�@�@ 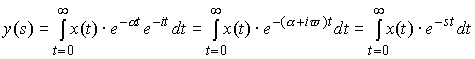 �������Ƌ��������܂Ƃ߂ĕ��f�����ƕ\�L�����܂��B�ϕ���0����n�܂��Ă���̂́A���v���X�ϊ��ł͈��ʊ��ƌ����Ď���0�ȍ~�̐M���݂̂��������߂ł��B ���̌W���ɂ��Ⴂ�f���ʏ�̂��ꂼ��̈ʒu�ɕ\�����Ă݂܂��傤�B �@�@�@�@�@�@�@�@�@�@�@ 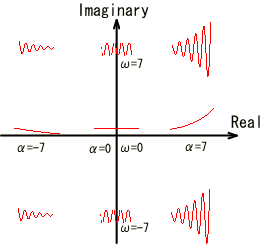 �����������g�����A�����������U�E������\���Ă��鎖���ǂ�������܂��B �@�@-------------------------------------------------------- �@�@�@�@�@�j���[�X�I�@�{�g�o�@�H�Ɛ��w���H�w�Ђ��o�ł���܂����B �@�@�@�@�@�@�@�@�@�@�@�@�@  �@�@-------------------------------------------------------- �@�ȉ��{���������̃_�C�W�F�X�g�ł��B�ڍׂ͖{���ɂĂ��m�F���������B������L�x�ɋL�ڂ���Ă���܂��B �@���A���Ђɂ͐����̓���m�F���r���������ɂ��X�e�b�v�o�C�X�e�b�v�Ŋw�K�\�ȍH�v�����Ă���܂��B ���v���X�ϊ��̓� ���v���X�ϊ��͉ߓn���ۂ̉�͂ɗ��p����܂��B���R�͉ߓn��͂ɕK�v�ƂȂ������������㐔�I�Ɉ����邩��ł��B����͈�ʓI�ɉ��Z�q�@�ƌĂ�鐔�w����ƂȂ�܂��B �Ƃ���Ń��v���X�ϊ�������n�߂čŏ��Ɋ������� �u�Ȃ����v���X�ϊ��Ŕ�����������������̂��H�t�[���G�ϊ��Ɏ����W�����𑫂��������Ȃ̂ɁB�����ĉ��ȂH�v �ł͂Ȃ��ł��傤���H �ȉ����̓���������Ƃ�ړI�Ƀ��v���X�ϊ����w�K���Ă݂܂��傤�B�܂��̓X�e�b�v���̃��v���X�ϊ�����ł��B ���v���X�ϊ��Ƃ� �ȉ��̂悤�Ɏ��ԃ[�����痧���オ�背�x���f�P�f���p������������j�b�g�X�e�b�v���Fu(t)�@�Ƃ����܂��B �@�@�@�@�@�@�@ 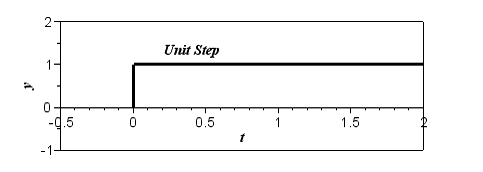 ���v���X�ϊ������ �@�@�@�@�@�@�@�@�@�@�@�@ 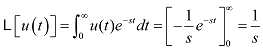 �傫�������̏ꍇ�� �@�@�@�@�@�@�@�@�@�@ �x�����ԃт̃X�e�b�v���̃��v���X�ϊ��� �@�@�@�@�@�@�@�@ 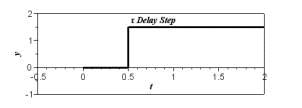
�@�@�@ 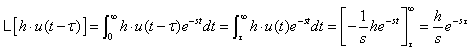 �@�@�@ �@�@�@ �ȏ��g�ݍ��킹�ĔC�ӂ̃p���X�����܂��B�@���Ƃ��A�ȉ��̂悤�ȑ傫�����ŕ��т̏ꍇ �@�@�@�@�@�@�@ 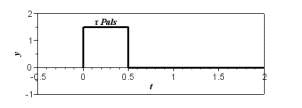 �[�����ԗ����オ��̃p���X�ɑ��A�ю��Ԓx�点�Ĕ��]�����p���X�𑫂����킹�� �@�@�@�@�@ �@�@�@�@�@ �ƂȂ�܂��B ���̂悤�Ȓ��q�ŐF�X�Ȏ��Ԋ��̃��v���X�ϊ����܂Ƃ߂�� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���v���X�ϊ��|�t�ϊ��\
���ꓙ��d�C��H�̉ߓn��͂ɉ��p���Ă݂܂��傤�B �ȉ��̂b�q��H������A���Ƀ��x�����ƂȂ��p���X�M����������ꂽ�ꍇ�̉����o�͂������߂܂��B �@�@�@�@�@�@�@�@�@ 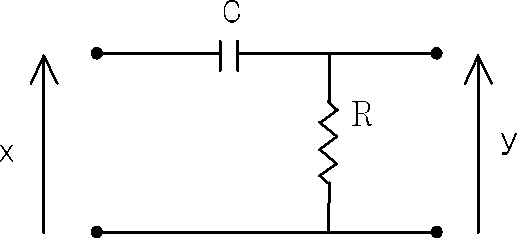 �L���q�z�b�t�̖@����� �@�@�@�@�@ �@�@�@�@ �@�@�@�@ 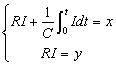 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �@�@�@�@�@�@�@�@�@ �@�@�@ �@ �������������������ɁA��������̂܂܃��v���X�ϊ����܂��B �@�@�@�@�@�@�@�@�@ �@�@ �@�@ ���ӂ������p���X�M���ł��胉�v���X�ϊ��w�� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �E�ӂ͐ϕ����Z���ϊ��\����E���� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ���E���ӂ����тx�ɂ��ĉ����ƁA �@ 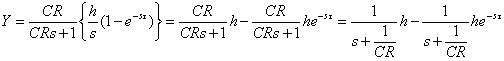 �@�@ �@�@���ꂪ���v���X�̈�ŋ��߂��㐔�������̉��ƂȂ�܂��B��A�����������������Ă��܂���B ��͎��Ԋ����ϊ��\�₻�̑g�ݍ��킹���t�������܂��B �@�@�@�@�@ �@�@�@�@�@ 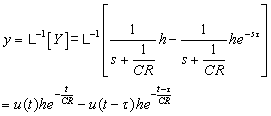 ����炵�����ԗ̈�ł̎w����������܂����B �����ł��B���ꂪ���v���X�ϊ��}�W�b�N�ł��I ����[�A�Ȃ�Ƃ������ł��ˁB ����̗�͂����P���Ȃ��̂ł������B�����ƕ��G�Ȕ����������ƂȂ���̂��A���l�̕��@�A�܂胉�v���X�̈�̑㐔�������ʼn������Ƃ��ł��܂��B �t�[���G�ϊ��Ɂ{�����������łǂ����Ă���Ȃ��Ƃ��ł���̂ł��傤���H �ȉ����̔閧��T���Ă݂܂��傤�B �������Z�̐��� �� �@�@�@�@�@�@�@�@ �ƂȂ�܂��B �܂�O�̊e���ɔ������Z�z���đ������Ƃ��ł��܂��B �������ȉ��̒ʂ�A�e�����O�p���ł���肠��܂���B �������Z���e���ɓK�p���ĉ��Z���邱�Ƃ��ł��܂��B �@�@�@�@�@�@ �@�@ �Ƃ��ŁA��������C�Â��ł��傤���H�@���̎��̓t�[���G�t�ϊ��Ɠ����`�������Ă��܂��B �܂莞�ԐM�����t�[���G�ϊ��ɂ����g���̈�ɓW�J���āA���ϕ����Z���e���i���g���ʂɕ��O�p���j�ɓK�p���邱�Ƃ��\�ł���A���̏ꍇ�͒P���ȎO�p���̔����ōς�ł��܂��Ƃ������Ƃł��B �����ĎO�p���̔��ϕ��͕��f�w�����ɒu�������ĕ\�������
�ł���Ai�ւ����ϕ����Z�q�̖��������Ă���A�������ăV���v���ȕ\���ƂȂ�܂��B �ȏ���C���[�W�Ŏ����ƁA �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�O�p���̔��ϕ� �@�@�@�@�@�@ 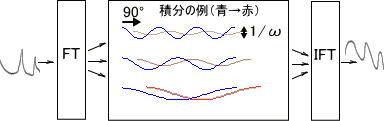 �Ȃ��A�����ł̓t�[���G�ϊ��E�t�ϊ���v���X�ϊ��E�t�ϊ��̊Ԃɂ���P/�i2�j�Ȃǂ̌W���͖{���I�Ȃ��̂ł͖����̂ŏȗ����ĉ�����܂��B ���āA���炽�߂ă��v���X�ϊ��\�����ϕ����m�F�����
����s=i��+���Ń�=0�ƒu�����ꍇ���t�[���G�ϊ��ƂȂ�̂ŁA�������Ƃ������Ă��܂��B�@ �܂胉�v���X�ϊ��Ŕ��ϕ��������\�͂͂��Ƃ��ƃt�[���G�ϊ��ɔ�����Ă����ƌ������ł��B �Ƃ���Ń��v���X�ϊ��̏ꍇ�͂ǂ�����[i��]�̑����[s]�ɂȂ�̂ł��傤���H �t�[���G�ϊ��̊��́A �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@[ei��t] �ł����B�@���f�\�����ꂽ�O�p���g�Q�ł��ˁB������������� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@i��[ei��t] ���̓��ɉ���Ă���[i��]��������Z�q���Ƒ����ł����킯�ł��B ���g���̈�ɕϊ����ꂽ���ԐM���́A�e���g���ʂ̊��ɑ��鐬���ɕ�������Ă��܂��B�e������������W�����A���g���̈�̐M���ɂ����邱�Ƃ́A���g���̈�̐M����������邱�ƂƓ����ɂȂ�킯�ł��B ������v���X�ϊ��̊��� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@[est] �ł��B��������� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@s[est] �ł��B�܂�[s]�����v���X�ϊ��ɂ�����������Z�q�ɂȂ镪���ł��B �g�����ꂽ���̖��� ���̓�́u�����ĉ��ȂH�v�ł����ˁB �t�[���G�ϊ������݂��邽�߂ɂ̓t�[���G�ϕ����L���l�Ɏ����i��Ύ����j����K�v���L��܂��B�t�[���G�ϊ��ŗl�X�Ȋ��ɉ��Z�q�@���g�����Ƃ���ƁA���X�K�p�͈͂������Ȃ�܂��B ���Ƃ��Ί��Fet�̃t�[���G�ϕ��͎������܂���B�������ȉ��̐}�̗l��e-��t��������Ǝ������܂��B���̗�ł̓�=2�Ƃ��܂����B �@�@�@�@�@�@�@ 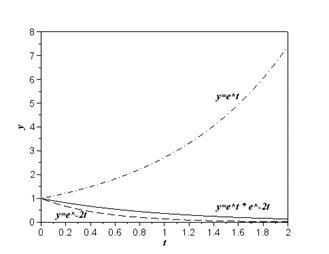 �E�E�E���X�����ł��ˁB ��������U�ϕ������������g���̈�ł̊����m�肷��i�܂胉�v���X�ϊ������܂�j�ƁA���g���̈�i���v���X�̈�j�Ő�قǂ̔��ϕ����̉��Z���{�����Ƃ��ł��܂��B�����Ă��̌�A�t�ϊ��ɂ�莞�Ԋ��ɖ߂������_�ŁAe+2t���|���邱�Ƃł��܂������Ă��܂��܂��B ���v���X�ϊ��Ŕ����������������闝�R�i�b��Łj �ȉ��̔����������ł����^����ꂽ�ꍇ�A���ɂ��ĉ������Ƃ��l�@���܂��傤�B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ [d/dt]�@��(t) = x(t) ���ԗ̈�̐M�����t�[���G�ϊ������X�y�N�g�������̂܂܋t�ϊ�����ƌ��̎��ԐM���ɂ��ǂ�܂��B�}�ɂ���Ƃ���Ȋ����ł��傤���B�@[ �E ]�͍s��A�x�N�^�Ƃ̗ގ������Î����Ă��܂��B �@�@�@�@�@�@�@�@�@�t�ϊ��i���j�@�@�X�y�N�g���@�@�@�@�ϊ��@�@�@�@�@���ԐM�� �@�@�@x(t)�@�@���@�@[�@ei��t�@]�@�@ ���@X(��)�@���@�@[�@e�|i��t�@] �@���@�@x(t) �ϊ��͂c�e�s�Ō����ƃt�[���G�ϊ��s������ԐM���x�N�g���Ɋ|���邱�Ƃɑ������A�t�ϊ��͊��s��Ɏ��g���M���i�X�y�N�g���j�x�N�g�����|���邱�Ƃɑ������܂��B���̏ꍇ�����͂Əo�͓͂������̂ɂȂ�܂��B �O�o�̔����p�t�B���^[i��]��}�����Ă݂܂��B �@�@�@�@�@�@�@�t�ϊ��i���j�@�@�����t�B���^�@�X�y�N�g���@�@�@�ϊ��@�@�@�@�@���ԐM�� �@x�f(t)�@���@�@[�@ei��t�@]�@�@ ���@�@[i��]�@�@�@X(��)�@���@�@�@[�@e-i��t�@] �@���@�@x(t) ���̏ꍇ�@x�f(t)�́@x(t)�̔����o�͂ƂȂ�܂��B �����Ō����ƁA �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@x�f(t) = [dx/dt] x(t) �ł��B �����ŁA�����p�t�B���^���t�������������t�B���^�Ɏ�ւ��Ă݂܂��B�X�J���[�Ȃ̂ŒP���ɋt���łn�j�ł��B �@�@�@�@�@�@�@�t�ϊ��i���j�@�t�����t�B���^�@�@�@�@�@�@�@�@�ϊ��@�@�@�@�@���ԐM�� �@��f(t)�@���@[�@ei��t�@]�@ �@�� [1/i��]�@�@�@�w(��)�@���@�@[�@e-i��t�@] �@���@��(t) ���̂�f(t)��������x�A�������Z�̑���ɖ߂��Ɓ@ �@x(t)�@���@[�@ei��t�@]�@���@[i��] �@��[1/i��] X(��)���@���@[�@e-i��t�@] �@���@x��(t) �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���@�@�@�@�@�� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�L�����Z�� ��f(t)�͋t�������^����Ă���̂ŃX�y�N�g���́��E���̒��̂悤�ɂȂ�܂��B���̂��������t�B���^[i��]���L�����Z����x(t)���o�͂��܂��B�܂���f(t)�����߂邙�ł����B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��f(t) �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ [d/dt]�@��(t) = x(t) �ȏオ�t�[���G�ϊ��ɂ��ȒP�ȂP�K�̔������������������J�j�Y���ł��B ���g���̈�ł͐M���i�X�y�N�g���j�̓X�J���[������Ă��邽�߁A����͑㐔���Z�ŋL�q����܂��B���鉉�Z���L�����Z�����邽�߂ɂ́A�P���ɋt�������Ηǂ������ł����A���܈�������킫�܂���B �������Z���t�B���^�Ƃ��đ�����ƁA�����������������s�ׂ́A�t�����t�B���^�ŕ⏞���鑀��ƍl�����܂��B���̗l�ɍl����Ə����͎������킭�̂ł͂Ȃ��ł��傤���B ���̗�Ɍ��炸�A��荂�K�̔������܂ޕ��G�Ȕ������������A���l�̎d�g�݂ʼn����܂��B�@�����āA�����ɂ͌ŗL�l�Ƌ��ʂ́A�ʔ����d�g�݂����݂���̂ł����E�E�E �ŗL�l�Ɠ`�B�� �ȉ��A�O�o�̔������Z�t�B���^�[�̐M���t���[�ł��B�@�����ɂ�闝�����₷���̂��߂Ƀ��v���X�̎��g���̈�ϐ��F s=i��+�� �ŁA����������0�Ƃ��ĉ�����܂��B �@�@�@ �@�@�@�@�@�@�@�@�@�@�@�@�`�`�`���g���̈�`�`�` �@x�f(t)�@��[�@ei��t�@]�@���o�@Y(��) ��[i��]�@��X(��)�@�p��[�@e-i��t�@] ��x(t) ���̒��ŁA�ȉ��̗l�ɕϊ��E�t�B���^�E�t�ϊ����܂Ƃ߂ĕϊ�W�ƒu�����ꍇ�A �@�@�@�@�@�@�@�@�@�@�@�@�@�@[W]=[ei��t]�E[i��]�E[e-i��t] [i��]��[W]�̌ŗL�l�ƂȂ�A[e-i��t]���ŗL�x�N�g���ƂȂ�܂��B����Ɏ��g���̈����[i��]��������Əo���ɒ��ڂ���� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@Y�i�ցj= i�ցEX(��) �̊W�����o���܂��B ���g���̈�ł̃t�B���^�W���͓��͂Əo�͂̔��\���A���g���̑㐔���Ƃ���H�i�ցj�ƕ\������܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@H�i�ցj = Y�i�ցj/X(��) = i�� ���̊�����ʓI�ɓ`�B���i���ۂ�H(s)�ł��E�E�E�j�ƌĂт܂��B�܂��ϊ�W���s��Ƃ����ꍇ�A�`�B����W�̌ŗL�l�Ƃ݂Ȃ����Ƃ��ł��܂��B ��H����R,L,C�����낢�뎝������ŁA��������ii�ցj��ϕ�����i1/(i��)�j���|�����葫������Ƒg�ݍ��킹�Ă����ƁA�`�B���͕����̌`���������ɂȂ�܂��B ��ʌ`�i�ȉ�������x�A�ϐ����ւ��炓�ɖ߂��Đ������܂��j�ŏ����ƁA �������^ �@�@�@�@�@��n=0�`N�@ans-n H(s) = --------------- �@�@�@�@�@��m=0�`M�@bms-m ���������^ �@�@�@�@�@�@�@(s-z1) (s-z2) �E�E�E(s-zn) H(s) = H0-------------------- �@�@�@�@�@�@�@(s-p1) (s-p2) �E�E�E(s-pm) ���������^�ŕ����s=p�ƂȂ�_�͋ɂƌĂ�A���́i���f���ʏ�́j�_�̈ʒu�͓`�B���̓����i�������U�E�U���j����͂����ŏd�v�ł��B�@ �������� �ȏ�A[���u]�H�Ɛ��w�Œlj����ꂽ�u���v���X�ϊ��̓�v�Ɋւ��đ������ł��B����g�o�ł͏��ЂƓ��l�A���ϕ����Z���\�ȗ��R������������������闝�R��������܂������A���X�蔲���_�C�W�F�X�g�łł��B�ڍׂɂ������̂�����͂��Љ��L�̂��w�������������������B�@�L�x�Ȑ}�⎖��A���̑����ǂ���A��R����܂��B �@�@-------------------------------------------------------- �@�@�@�@�@�j���[�X�I�@�{�g�o�@�H�Ɛ��w���H�w�Ђ��o�ł���܂����B �@�@�@�@�@�@�@�@�@�@�@�@�@  �@�@-------------------------------------------------------- �G�k�F���v���X�ϊ��\�̒��ߕ� ���v���X�ϊ��̕\���ۈËL����̂������̂ł����A�e���ڂ̊֘A���ɒ��ڂ���Ɩʔ������ƂɋC�Â��܂��B���̕��o���₷����������܂���E�E�E ��u(t)�̊W �@�̃��v���X�ϊ���[�P]�ł��B�͐ϕ�����ƃ��j�b�g�X�e�b�v��u(t)�ɂȂ�܂��B �����Ń��v���X�̈�ɂ����郆�j�b�g�X�e�b�v���́A�̃��v���X�ϊ�[�P]�ɑ��ϕ����Z�q[1/s]���|���������̂ƍl����Ɣ[���ł��܂��B �@�@�@���ԗ̈��@�@�@�@�@�@�@�@�@�@�@���v���X�i���g���j�̈� �@�@�@�@�@�@�@�@�|�����v���X�ϊ������@�@[�P] �@�@�@�@�@�@�b�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�b �@�@�@�@�q�ϕ��F��r�@�@�@�@�@�@�@�@�@�@�@�q �ϕ��F1/s�@�r �@�@�@�@�@�@���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �@�@�@�@�@�@u(t) �|�����v���X�ϊ������@[�P][1/s] u(t)��e-at�Ƃ̊W �@�t�[���G�ϊ��̎��g������[i��]�ŋ�������ɌŒ肳��Ă��܂����B���v���X�ϊ��ł͈ȉ��̗l�ɁA���������烿���ꂽ�c�������g�����Ƃ��Ď�邱�Ƃ��ł��܂��B �@�@�@�@�@�@������[i��]�@�@�@��=2�@�@ �@�@�@�@�@�@�@�@�@�@�� �@�@�@�@�@�@�@�@�@�@ |�@�@�@�@�@�@�F�@�@�@ �@�@�@�@�@�@�@�@�@�@ |�@�@�@�@�@�@�F�@�@�@ �@�@�@�@�@�@�@�@�@�@ |�@�@�@�@�@�@�F�@�@�@ �@�@�@�@---------------------���@������[��] �@�@�@�@�@�@�@ �@�@�@|�@�@�@�@�@�@�F�@�@�@ �@�@�@�@�@�@�@�@�@�@ |�@�@�@�@�@�@�F�@�@�@ �@�@�@�@�@�@�@�@�@�@ |�@�@�@�@�@�@�F�@�@�@ �����ŁA���Ƃ���=2�ƌŒ肵�Ă݂܂��B��������Ǝ��g�������͋���������2�͂Ȃꂽ������ƂȂ�܂��B���̏ꍇu(t)�̃��v���X�ϊ�[1/s]�͂��̒�������ňȉ��̗l�ɒ�`���ꂽ���ƂɂȂ�܂��B �@�@�@�@�@�@�@��=2�ł�u(t)�̃��v���X�ϊ��F�@[1/�i2+i�ցj] ���Ƃ��ƃ��͐ϕ������p�Ɋ|����w�����̈��k�W���ł���A�t�ϊ����ɓ����l�ŕ������]�����Ċ|����ƁA�L�����Č��̎��Ԋ��ɖ߂��܂��B�i�����Œ肵�ĕϊ��E�t�ϊ����鎞�̗Ⴆ�ł��j ����ɑ��āAu(t)�̃��v���X�ϊ���A�܂�[1/�i2+i�ցj]�ɁA����Ɏ�����2��[�{a]�Ƃ���ƁA[1/�i2+a+i�ցj]�B�@������t�ϊ�+�L�����Ă��]�v��a�̕��������ɖ߂炸u(t)���w�������i���邢�͎w�����U�j���邱�ƂɂȂ�܂��B �t�Ɍ����ƁA�w�����̃��v���X�ϊ���u(t)�̃��v���X�ϊ�[1/s]�ɂ����Ď������ɃI�t�Z�b�g��[+a]�����������̂ƍl�����܂��B�����}�ɂ���ƁA �@�@�@�@�@u(t) �@�|�����v���X�ϊ������@�@[1/s] �@�@�@�@�@�@�b�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�b �@�@�q�w�������E���U�r�@�@�@�@�@�@�@�@�q �������I�t�Z�b�ga�@�r �@�@�@�@�@�@���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �@�@�@[�@e-at�@]�@�|�����v���X�ϊ������@[1/(s+a)] e-at��sin�Ccos�Ƃ̊W �@����͈ȉ��̗l�ɃI�C���[�̌����ɂ��A�݂��ɋt��]���镡�f�w�����̘a�ƍ��ł���킳��܂��B �@�@�@ 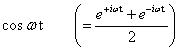 �@�@�@ �@�@�@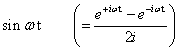 ���Ƒf���Ȃ�e-at�̉��p��ł����B ���w���h�P�h����n�܂����H�l�ɁA���v���X�ϊ��̓���n�܂����H�ƌ�����̂�������܂���B �������� ���ϊ� �@�@-------------------------------------------------------- �@�@�@�@�@�j���[�X�I�@�{�g�o�@�H�Ɛ��w���H�w�Ђ��o�ł���܂����B �@�@�@�@�@�@�@�@�@�@�@�@�@  �@�@-------------------------------------------------------- �@�@�ȉ��Az�ϊ��̑������̊T�v�������lj����܂��B ���U�t�[���G�ϊ��iDFT�j�ɂ��A�f�W�^���M�������̊�Ղ��������Ƃ����܂��B ���U���ԐM���◣�U���g���M��������Ԃ̕ϊ��Ƃ��Ĉ�����悤�ɂȂ�܂����B �t�[���G�ϊ���v���X�ϊ��ŋc�_���Ă��������������͐����ǂ̂悤�Ɉ�����̂ł��傤���H ���������� �ȉ��̍������������A���V�X�e���̔����������ɑΉ����܂��B ���������̗�F x�̓��͂ɑ���a�{�̂����o�͂������`�V�X�e���o���p��z�肷��� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@x[n]���oh�p��y[n] �������ł́A �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@y[n]=a�Ex[n] ���̏ꍇ�A�V�X�e���̉�͂͊ȒP�ł��B���͂Əo�͂͒P���ȃX�J���[�{�ł��B ����ł́A���̃V�X�e���ɑ�1�����O�̏o�͂̂��{�������Ă݂܂��傤�B �������ł́A �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@y[n]=a�Ex[n]+b�Ey[n-1] a=0.7, b=0.3�̏ꍇ����v�Z�i�\�v�Z�ɓ����ƊȒP�ł��j�ŃV�~�����[�V�������Ă݂܂��傤�B �@�@�@�@�@�@�@�@�@�@�@�@���j�b�g�X�e�b�v�����͗� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@x[n]�@�@�@y[n-1]�@�@�@y[n] �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@a�@�E1 �@+�@ b�@�E0 �@�@= �@0.7 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@a�@�E1 �@+ �@b�@�E0.7 �@= �@0.91 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@a�@�E1 �@+ �@b�@�E0.91 = �@0.973 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�F�@�@�@�@�@�@�@�F �@�@�@�@�@�@�@�@�@�@�@�@�@�P�ʃC���p���X�i�j���͗� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@x[n]�@�@�@y[n-1]�@�@�@y[n] �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@a�@�E1 �@+�@ b�@�E0 �@�@= �@0.7 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@a�@�E0 �@+ �@b�@�E0.7 �@= �@0.21 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@a�@�E0 �@+ �@b�@�E0.21 = �@0.063 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�F�@�@�@�@�@�@�@�F a=0.7, b=-0.3�̏ꍇ �@�@�@�@�@�@�@�@�@�@�@�@�@�P�ʃC���p���X�i�j���͗� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@x[n]�@�@�@y[n-1]�@�@�@y[n] �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@a�@�E1 �@+�@ b�@�E0 �@�@= �@0.7 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@a�@�E0 �@+ �@b�@�E0.7 �@= -0.21 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@a�@�E0 �@+ �@b�E-0.21�@= �@0.063 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�F�@�@�@�@�@�@�@�F �ς��ƌ��A�ߓn�������̂��́I�E�E�E�Ɍ����܂��H �����������Ɠ��l�A�ω��̓x������\���W�����܂�ł��܂��B �@���̉ߓn�������ǂ��ƃA�i���O��H�̉ߓn�����̗ގ����ׂ邽�߂ɁA�ȉ��̂悤��RC�ɂ����`�V�X�e���A�܂�A�i���O�t�B���^�[���l���܂��B �@�@�@�@�@�@�@�@�@�@�@ 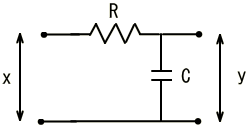 ���͓d����E���A�o�͓d����E���Ƃ���ƁA�ȉ��̊W���ƂȂ�܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@ ���̎��̒��̒�RR�ɂ��h���b�v�d��ER�͈ȉ��ɂ�苁�܂�܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@ 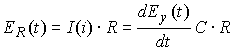 ����āA�ȉ��̐��`���������������߂��܂����B �@�@�@�@�@�@�@�@�@�@�@�@�@�@ 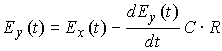 ���̎��ɂ����āA�W����K���Ɏ��ƁA�ȉ��̗l�ɗ��U���ԁi�����j�̐��`�����������ɋߎ��ł��܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �ȏ�̍l�@�ɂ��A�u���ԃV�t�g�������W���v�̗l�Ȃ��̂ŕ\�����ꂽ�����������́A���U���ԐM���ɂ�����t�B���^�[��\�����Ă���ƁA�����邱�Ƃ��ł������ł��B �A�i���O�t�B���^�[�̉�͂ɁA�������������������Ƃ��K�v�ƂȂ�A���v���X�ϊ������͂ȃc�[���ƂȂ�܂����B���l�Ɂu�����������p���v���X�ϊ��v���L��Ɗ������Ȃ�܂��ˁI�@ �E�E�E�ƁA���̗l�ȓ��@�H�ɂ��A���v���X�ϊ��̎������U�����s���Ă݂܂��傤�B �T���v�����O�����ss�Ƃ��ĕ��f�w�������ȉ��̗l�ɂ��Ƃ����܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ��������ƁA���v���X�ϊ��̗��U�ϊ��łƂ��Ĉȉ��̎��܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ���̕ϊ������ϊ��Ƃ�т܂��B �����A���j�b�g�C���p���X��[n]�̂��ϊ������߂Č��܂��傤�B �@�@�@�@�@�@�@ 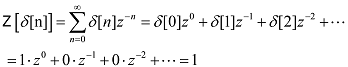 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�����@ZT-1 �@�@�@�@�@�@ ��������Ɓ@Z[��[n]]=1�@�����܂�܂����B �p���X��x�点���ꍇ��Z[��(n-1)]�ł͂ǂ��ł��傤���H������ �@�@�@�@�@�@�@�@�@�@�@�@�@�@Z[��(n-1)]=z-1 �ł��B ��L�����@ZT-1�̕ϊ����p���X�̈ʒu���E��k���炷��z-k�ƂȂ邱�Ƃ͖����ł��B �Ƃ������ŁA���Ȃ��Ƃ���[n]�Ɋւ��Ă͈ȉ������藧���܂��B �@�@�@�@�@�@�@�@�@�@�@�@Z[��(n-k)]=Z[��[n]]�Ez-k �@�@�@�@�@�@�@�@�@�@�@�@�@�@�����@ZT-2 ���R�t�����i�p���X�ʒu��i�߂�j�́A �@�@�@�@�@�@�@�@�@�@�@�@Z[��(n�{k)]=Z[��[n]]�Ez-k �����藧���܂��B�������A�ڍׂ͏ȗ����܂����A��̂ƂȂ������v���X�ϊ��̒�`�Ɠ��l�ɂ����ʊ��Ɍ��肷��K�v������A����0����ɐH�����M����0�ɂȂ�悤�ȕ���K�v�ƂȂ�܂��B ���Ƀ��j�b�g�X�e�b�v���̂��ϊ������߂Č��܂��傤�B �@�@�@�@�@�@ 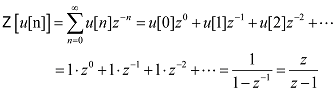 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�����@ZT-3 �ƁA���܂�܂����B ���������@ZT-2�����̕ϊ��ɂ����藧�������Ă݂܂��傤�B���ԗ̈�̔C�ӂ̊��͘A������C���p���X�̏W���́i�����\���ł���ݍ���u(n)*��(n))�ƍl�����܂��B�ɐ��藧���̎��Ԑ��ځi�x��E�i�݁j�̌����͂��̏W����u�ɂ����藧�͂��ł��B �����@ZT-3�ɂ����āA�P�����x��̃��j�b�g�X�e�b�v��Z[u[n-1]]�ł́A��P�����[���ƂȂ�܂��B���������� �@�@�@�@�@�@�@�@�@�@�@Z[u[n-1]]=Z[u[n]]-1=z/(z-1)-1=1/(z-1) ����Az-1���|�����ꍇ�� �@�@�@�@�@�@�@�@�@�@�@Z[u[n]]�Ez-1=�oz/(z-1)�p�Ez-1=1/(z-1) �ƁA��v���܂����B��u(t)�ł����Ԑ��ڑ������藧���Ă��܂��B �����ł͊ȒP�ȗᎦ�݂̂Ƃ��܂������A����z-1�͎��Ԓx�����Z�q�ƌ����Ă悢�ł��傤�B�����Ă��̉��Z�q�͔��ɏd�v�ł���f�W�^���t�B���^�[�̊�b�ƂȂ���̂ł��B�Ȃ��Ȃ炱��ɂ�荷����������\���ł��邩��ł��B �Q�D4�@�t�B���^�[�̊�b ���v���X�ϊ��̓`�B���̑������^�\�L�������C�����Ă��ϊ��p�Ƃ��܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@ 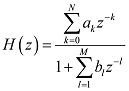 ����̑�ꍀ���P�Ƃ��܂����B�`�B���͏��F���W���Ȃ̂ŁA���̂悤�ɒ�`���Ă����ɖ�肠��܂���B ������g�������g���̈�ł̕\���� �@�@�@�@�@�@�@�@�@�@�@�@�@ �ł���A�`�B��H�̒�`���������A�ό`����� �@�@�@�@�@�@�@�@�@�@�@�@ 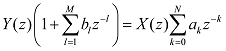 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �@�@�@�@�@�@�@�@�@�@�@�@ ������z-k���x�����Z�q�ł��邱�Ƃɒ��ڂA�S�̂��t�ϊ����܂��B �@�@�@�@�@�@�@�@�@�@�@ ����I�@�Ȃ�ƁA����͍����������ł́H �ƁA���̗l�Ɏ��g���̈�ŕ��i��g�ݍ��킹�ċ@�\�v���A���̌W�����ȉ��̂悤�Ɏ��ԗ̈�ɓW�J���邱�Ƃ��\�ƂȂ�܂��B 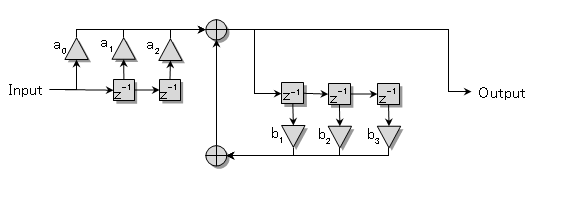 a�̓t�B�[�h�t�H�A�[�h�̌W���Ab�̓t�[�h�o�b�N�W���A������z-1�̔��͂P�����x����\���܂��B ������L�̍\����Scilab�Ŏ������Ă݂܂��傤�B �ȒP�ȗ�Ƃ��đO�o�̍�������������v�Z�������F��O���t�B�[�h�t�H�A�[�h�W����0.7�A��1���t�B�[�h�o�b�N��-0.3�Ƃ��P�ʃC���p���X����͂��܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@dfilter.sci�@�@�\�[�X�v���O�����i�E�N���b�N�ŕۑ��j �ȉ��C���p���X�ɑ��鉞�����V�~�����[�V�������Ă��܂��B �@�@�@�@�@�@�@�@�@�@�@ 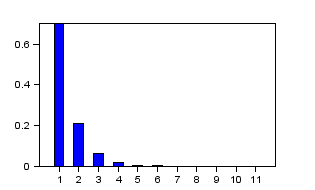 �A�i���O��H�̉����ł�����݂̏o�͌��ʂƂȂ�܂����B��������v�Z�̌��ʂƂ���v���Ă��܂��B���A������������ł̂��̒�`�̓v���X�}�C�i�X�t�ɂȂ��Ă���̂ł����ӂ��������B �t�B���^�Ə�ݍ��݂̊W �@������`�V�X�e���ɂ����āA�P�ʃC���p���X���͂ɑ���C���p���X�������ȉ��̗l�i�ł���߂Ȑ��l�ł����E�E�E�j�ɋ��܂��Ă����Ƃ��܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ���͊����ȉ��̒ʂ�Ƃ��܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �o�͈͂ȉ��̒ʂ�A��ݐϕ��̗��U�M���łł����ݍ��ݘa�ŋ��߂��܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ��ݍ��ݘa�̕M�Z���@�ł��B�ӊO�ɊȒP�ɂł��̂Ő���A�����Ă݂Ă��������B �@�@�@�@�@�@�@�@�@�@ 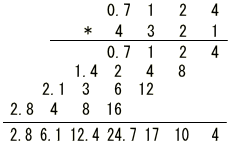 ���ǁA�o�͂��i���j�͈ȉ��̒ʂ�ƂȂ�܂����B �@�@�@�@�@�@�@�@�@ �m�F�̂���scilab�ŏ�ݍ��ݘa�̊��Flconv(g,x)������Ă݂܂����B �@�@�@�@�@�@�@�@�@�\�[�X�v���O�����@�@�@SciLab_src_lconv �ȉ��A���s���ʂł��B �@�@�@�@�@  ���i���j�Ax(t)���ꂼ��̎��g���̈�\��(���̏ꍇ�͂��ϊ��j��G�iz)�AX�iz�j�Ƃ���ƁA �@�@�@�@�@�@�@Z-1[�@G�iz)�EX�iz�j]�@=�@���i���j*x(t)�@ G�iz)���t�B���^�̓�����\���`�B���Ƃ݂Ȃ��܂��B���̂��Ƃ͂��ϊ��Ɍ��炸�A�t�[���G�ϊ���v���X�ϊ��ł����l�̂��Ƃ������܂��B ���g���̈�\���iFrequency-domain representation) �@���̓t�B���^�[�̎��g�����������ϊ��𗘗p���ĕ��͂����Ă݂܂��傤�B �@�@�@�@�@�@�@�@�@�@�@�@�@�@ �����ŁA��=0�Ƃ����ƁA���ϊ��̓`�B��H(z)�͗��U���ԃt�[���G�ϊ��iDTFT)�ɂ��`�B��F�i�ցj�Ɠ��l�ƂȂ�܂��B���������āA �U�������� �@�@�@�@�@�@�@�@�@ �ʑ������� �@�@�@�@�@�@�@�@�@ �f�[�^��̓��o�͂ƁA�����̌W���ł��ׂĂ����܂�܂��B�T���v�����O����Ts�͕K�v�ȂƂ��Ɉӎ�����悢�̂�Ts=�P�Ƃ��ւ𐳋K���p���g���i-�`��[rad/s]�j�Ƃ��Ĉ����܂��B ���������Ď��ԗ̈�ł̃t�B���^�̌W�����w�肳��āA���̓�����m�肽���ꍇ�́A �@�@�@�@�@�@�@�@�@�@�@ 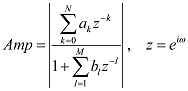 �@�@�@�@�@�@�@�@�@�@ 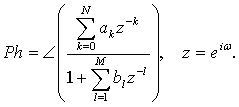 �@ �@���v�Z����Ηǂ����ƂɂȂ�܂��B ��̓I�ɂ͏�L�̎��Ɋe�W�������蓖�āA���̕��f�w���ւ̑g�ݍ��킹����͓I�ɉ����i�c�[���Ƃ��Ă�Maxima�Ȃǂ̐�����̓\�t�g���g���H�j�Ȃ�A�ւ�Scilab���ŗ��U�I�ɃX�C�[�v����Γ�����m�邱�Ƃ��ł��܂��B ��P�j�@���ԗ̈�ł�1���A�Ҍ^�t�B���^�[�̗�Ɠ��l�A�ȉ��̒ʂ�Ƃ��܂����B �@�@�@�@�@�@�@ ��0���t�B�[�h�t�H�A�[�h�W���F�@b0=�@0.7 �@�@�@�@�@�@�@�@�@�@��1���t�B�[�h�o�b�N�W���F�@a1=-0.3 Maxima�ɂ�鐔���x�[�X�̉���@�E�E�E[���u]�H�Ɛ��w���f�ځi�⑫�ł��j �ȉ��̗l�ɁA�قڐ����̒ʂ�L�q���邾���ŊȒP�ɓ��������܂�܂��B
���U�������A�Ԃ��ʑ������ł��B�����͐��K���p���g���ł��B Scilab�ɂ�鐔�l��� �@�@�@�@�@�@�@�@�@�@�@respfreq�@Scilab �\�[�X�v���O�����i�E�N���b�N�ŕۑ��j �@�@�@�@�@�@�@�@ 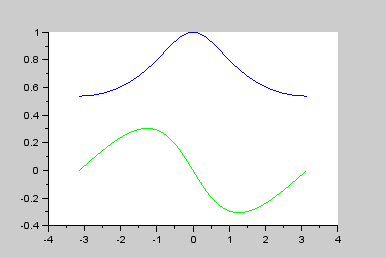 ���U�������A���ʑ������ł��B�����͐��K���p���g���ł��B Scilab�ɂ�鐔�l��͂ł�Maxma�Ɠ��l�̌��ʂ܂����B ��Q�j�@3�����A�Ҍ^�t�B���^�[�̗�ł��B �@�@�@�@�@�@�@�@�@�t�B�[�h�t�H�A�[�h�W���F�m1�C�R�C�R�C�P�n/�W �@�@�@�@�@�@�@�@ �@�@�@�t�B�[�h�o�b�N�W���F�O Scilab�ɂ�鐔�l��� �@�@�@�@����L��P)��Scilab�̃R�[�h��A�R�����g�A�E�g���Ă���s��L���ɂ��Ď��s���Ă��������B �@�@�@�@�@�@�@�@�@�@ 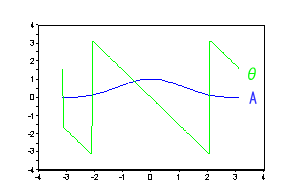 �@�@-------------------------------------------------------- �@�@�ȏ�A �@�@-------------------------------------------------------- |
| �O�̃y�[�W | �@�@�ڎ��@�@�@ | ���̃y�[�W |