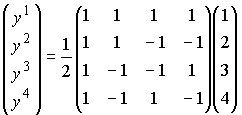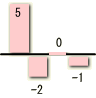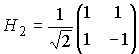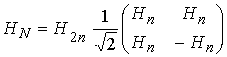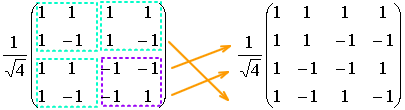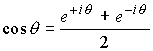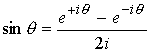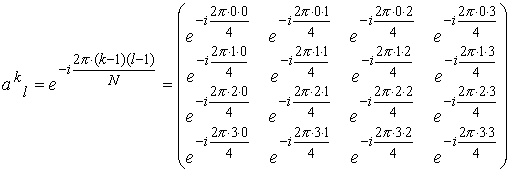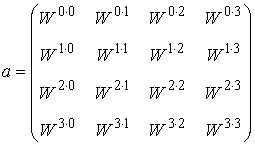ニュース! 本HP 工業数学が工学社より出版されました。

はじめに
数値計算のツールとしてMatlabにかなり近いフリーソフトのScilabを利用します。けっこう使えます。興味のある方はダウンロードしておいてください。
参考HP MATLAB つかいませんか
1.直交変換
1.1 直交基底
『次の連立方程式を解け!(ただしxの肩の上付き数字は累乗ではなく、添字)』
きっと中学校あたりの数学の問題です。
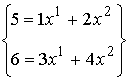
答えは
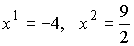
ですね。当時めんどくさくも頑張って解いていたような記憶があります。今の答えは数式処理でらくらく回答させました。
これを行列・ベクトルの式であらわすと、
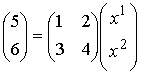 → → 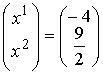
勿論、[5,1,2]や[6,3,4]という数字の組み合わせも、全く任意に選べます。(ただし[5,1,2]に対し[10,2,4]のような場合は連立方程式ではなく、同一の式ですから除外します。)
これらを行列の一般型で書くと
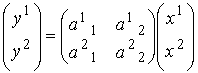
となります。これはベクトル/行列の演算としてドット積(内積)
y=a・x
と書くことが出来、さらに成分表示では縮約として
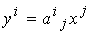
と現されます。
アダマール変換の準備のためにちょっと見方を変えてみましょう。aを行ベクトルに分けてみます。
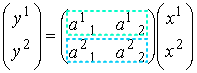
この場合『xベクトルをaの行ベクトルでyに変換する』式と見れます。変換ベクトルを組み合わせて任意のyを生成できます。
xを入力信号とし、変換ベクトルの組み合わせで任意の出力ベクトルyを合成できるわけです。逆は真でしょうか? つまりyを任意に取り、かつ変換ベクトルも任意の場合、入力ベクトルを決定できるのでしょうか?
勿論連立方程式の解が求まる訳ですから真です。つまりy、aの方を任意に決めてxを求める事が出来ます。連立方程式が解けるからです。
ここでaは任意なので以下の様に選んでも問題ありません。
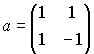
そうすると、この場合
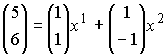
となります。連立方程式を解くと
x1=11/2, x2=-1/2
が解となります。
ところでこの場合、いちいち連立方程式を解かないで済む、非常に簡単なxの求め方が存在します。以下の様にyの成分と右辺の列ベクトルとの積和を求めて見ましょう。
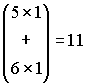 , , 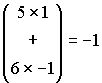
いきなり解の2倍の値が求められました。何だかキツネにつままれたようです。
じつは、秘密はaを構成している行ベクトルが直交基底ベクトルであると言う処に有ります。
この直交基底を並べた行列aはユニタリー行列と言われる特殊な行列です。連立方程式の解を求めるということは逆行列を求めることに等しい操作です。
ところがユニタリー行列は転置(行と列を入れ替える)し、さらに複素共役を取ると逆行列と等しい、つまり
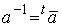 (実数の場合 (実数の場合 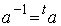 ) )
という便利な行列です。この場合aは実数なので、xを求めるのに以下の様にaを転置でひっくり返して内積(つまり積和演算)を取るだけで簡単に求められるわけです。
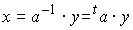
先ほどの計算もこの式を利用していました。ただ、2倍になったりしているのでもう少し行a選び方を工夫しなければ完全なユニタリー行列といえません。
以下、アダマール変換でもう少しこの方法を検討してみましょう。
1.2 アダ-マール変換
連立2次から4次に拡張してみましょう。
以下の様に直交基底を行ベクトルとします。
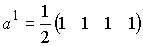 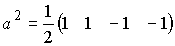
 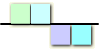
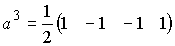 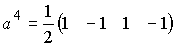
 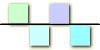
これを縦に並べて
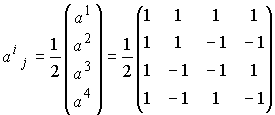
変換行列aとします。
次にyを任意の解析すべき入力信号と考えます。今回のこぎり波に模して
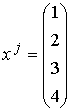 → → 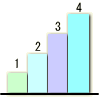
としましょう。
変換式
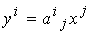 (行列で表現すると (行列で表現すると 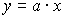 ) )
は
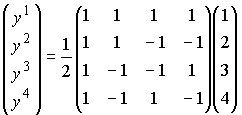
結果はy=[5,-2,0,−1]となり、こぎり波状の入力信号xを変換行列aにより変換した形となります。
変換行列を構成する四つの直交基底を波として眺めてみましょう。[+1+1+1+1]は直流でしょうか。最後の[+1-1+1-1]は2Hzの波の様に見えます。
このイメージを持ったまま、もう一度この演算における操作を確認てみましょう。
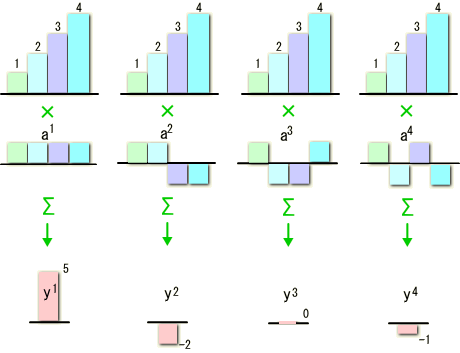
周期波a1〜a4それぞれの時間軸方向にそって入力信号と掛け合わせてその合計をとっています。
この様な操作で出力yの各成分は、何の意味があるのでしょうか?
実を言うと、直交基底ai対するスペクトルと見ることが出来ます。それぞれの波(もどき)にこのスペクトルと思われるyをかけて、その結果を合成してみましょう。
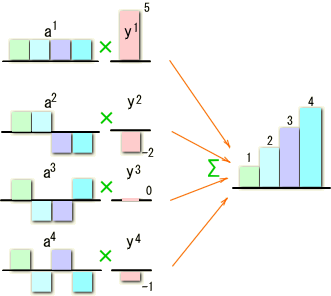
元の入力波形が再現できました。 どうやらスペクトルと言って良いようです。
この操作は行列の式で現すと
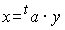
となります。なぜなら、上記の図を良く眺めてみると、足しこむ方向がaの縦方向であることが理解できます。つまりaの転置行列と内積を取っているわけです。
ところが変換行列aは、連立方程式を解いていただければ納得出来るように、
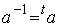
となるユニタリー行列です。結局この操作は以下の式の通り逆行列と内積を取る操作であったことになります。
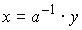
つまり逆変換式です。
以下に変換式と逆変換式の関係をあらためて整理しておきます.
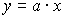 → →
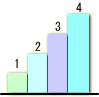 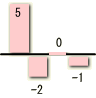
時間軸 ← 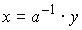 周波数軸? 周波数軸?
一般型として変換行列を以下の様に定義したものがN次のアダマール行列です。
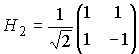
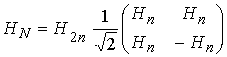
アダ-マール行列にはこの定義通りのものをナチュラル型、符号の変化する回数の少ない行順に並べ替えたものをウォルシュ型とよびます。
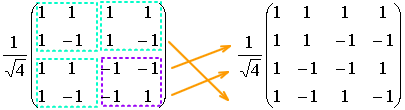
ナチュラル型 ウォルシュ型
勿論、この変換行列aの逆行列は転置行列と等しいという、以下のユニタリー行列の条件を満たす様に係数を選んでいます。
ユニタリー行列の条件
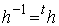 (複素数の場合: (複素数の場合: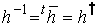 ) )
しかも、アダマール行列は以下の通り、転置前と転置後が等しいエルミート行列ででもあります。
エルミート行列の条件
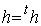 (複素数の場合: (複素数の場合: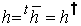 ) )
無線通信の新しい方式であるCDMAでは、このアダマール・ウォルシュ行列の行ベクトル一つ一つを拡散符号と見なして直交変調を行い多重化を実現しています。
1.3 離散コサイン変換(DCT)
N次の変換行列に対して
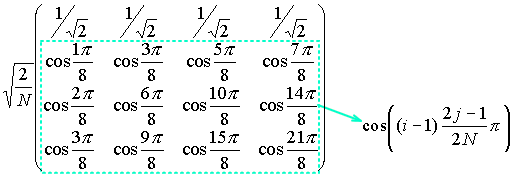
を使うと離散コサイン変換(DCT)となります。
第1行は直流成分(DC成分)であるため実効値を交流と合わせるために1/√2と決められています。2行以下の交流成分がCos関数で定義されています。
勿論、この変換行列もユニタリー性
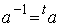
の条件を満たします。ただし、残念ながらアダマール行列と異なり転置行列は元の行列とは異なってしまいます。
N=8の変換行列をSciLabで確認してみましょう。
ソースプログラム SciLab_src_DCT
SciPadに貼り付けExecuteすると以下のグラフを表示します。
X軸に沿って0がDC(直流)成分で、以降Cos波が徐々に周波数を高くしながら続いているのが分かります。
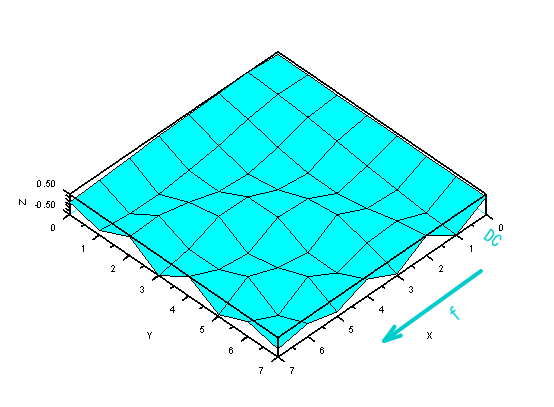
尚、SciLabのコンソールではユニタリー性の確認のため逆行列と転置行列の差分を表示しています。

数値処理なので完全に0とはなりません。10の-15乗の精度で一致しています。
前節でアダマール変換は周波数もどき空間への変換と説明しましたが、ここまで来れば立派な周波数空間でしょうか。後ほど説明するフーリエ変換・DFTへの通り道程度にイメージして下さい。
DFT(離散フーリエ変換)の実数部を使った展開がDCTに相当します。実数部以外に何が有るのかと言うと、虚数部・サインの項となります。
このDCTは画像処理との相性が良く、画像の周波数成分上、低周波域にパワーを上手に偏らせてくれます。この特質を利用してJPEG/MPEG等の静止画部分の圧縮に利用されています。
以下、N=4のアダマール変換(のこぎり波入力)と比較のため、Scilabのプログラムで変換を行ってみました。
 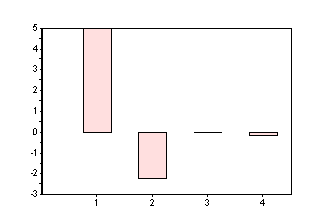
ソースプログラム SciLab_src_DCT4
うーむ。アダマール変換に比べてほとんど同じに見えます・・・が、高周波数域の係数がやや小さめでしょうか。
1.4 離散フーリエ変換(DFT)
離散コサイン変換からさらに、時間・周波数領域変換のスタンダードと言うべきフーリエ変換に進みましょう。考え方はCos波で作った変換行列にSin波の組を追加するだけです。
DCTが下の青でプロットしたCos波だけであったのに対し、緑のSin波を追加することになります。
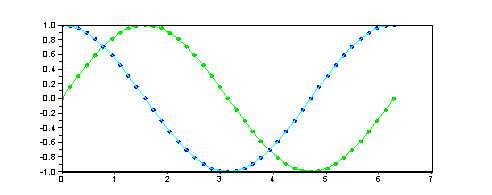
Cos波とSinは同一周波数でも直交しています。数式で表すと
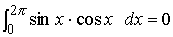
となります。
任意の位相のサイン波は同一周波数のSin/Cosのペアで表される直交成分に展開できます。つまり『この波は6割方Sin寄り、4割がCos』だとかです。見るからに離散コサイン変換よりきめが細かそうです。
しかしこのままだとCos分、Sin分と、変換行列が2個分になってしまい扱いが面倒くさくなりそうです。
そこで複素表現が登場してきます。工学の世界では虚数や複素数は便利なので道具として利用されています。しかし物理学の世界では物理量の構成要素として根源的なものとなります。
(物理に興味のお有りの方は AcademiaNotes Scienceコーナー を。 相対性理論や量子論では物理量に虚数が現われてきます)
そもそもCosとSinが組み合わされば、回転を表現する事が可能となります。そして複素空間での回転は以下の様に指数に複素角で表現されます。
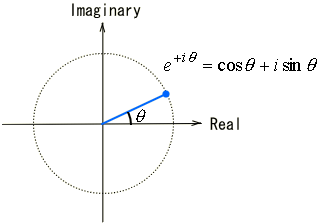
複素指数関数とよばれ、正にフーリエ変換にぴったりの表現方法でしょう。
回転の周波数をf とし角周波数をωとすると、
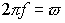
位相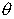 との関係は との関係は
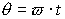
よって回転運動は
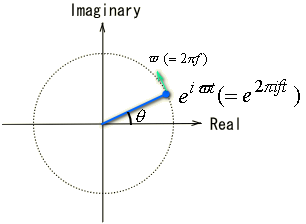
と表現されます。
今度は逆に、Sin・Cosを複素指数関数で表してみましょう。
Sin運動は正の複素角回転と、逆回りの複素回転との和で表されます。Cos運動も同様に正の複素角回転と、負の逆回りの複素回転との和で表されます。
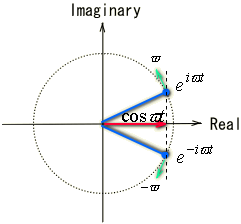 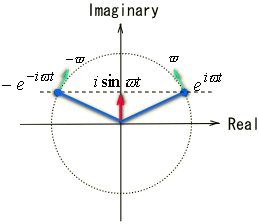
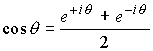 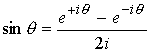
そして、これはオイラーの公式そのものです。
れでは、離散コサイン変換と同様に、離散フーリエ変換のN=4の場合の変換行列を示します。
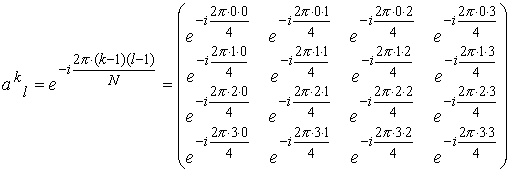
離散コサイン変換の行列より、Sinの項が増えているのが分かりますか?納得できない場合は [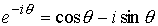 ] の式を当てはめて、もう一度ながめてみてください。 ] の式を当てはめて、もう一度ながめてみてください。
変換式は以下の通りアダマール変換やDCTと同様です。
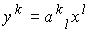
全部書くと以下の通りです。変換行列の要素を整理して、見やすくしておきました。
入力xはお馴染みののこぎり波の例です。
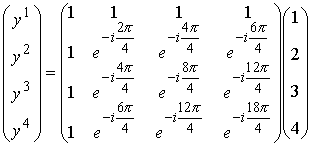
変換行列部を複素平面表示に表示しておきます。
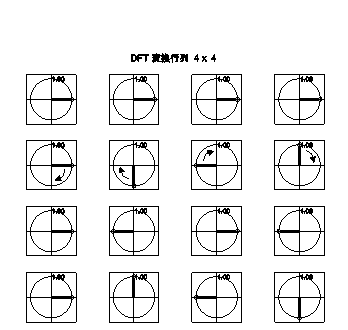
この様に変換行列は回転する複素指数関数を要素として持つ列ベクトルが縦に並んだ構造になっています。
回転方向は右回り(負)であり、入力信号ベクトルxと内積をとると、と入力信号中に存在する同一周波数の正方向(左回り)の成分を抜き出すことができます。
各行は直行する周波数を代表しているので、行列とxの積の結果は周波数成分が縦に並んだベクトルyとなります。なお、下半分は上半分の逆回転となっていて負の周波数を代表しています。ただし、3番目は最高周波数であり正の周波数と負の周波数どちらとも解釈できます。
当然変換結果は複素数であるので、RealパートとImagパートに分けて表示します。
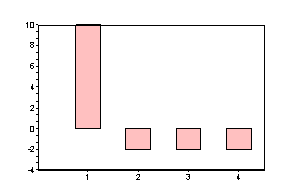
Realパート
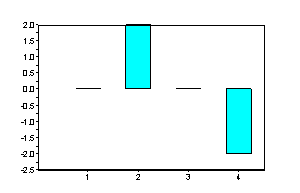
Imagパート
Real,Imag合わせて絶対値によるスペクトルを示します。
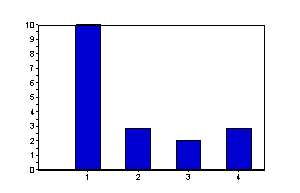
絶対値:|y|
対象的で
ステレオのグラフィックイコライザーでお馴染みの表示方法です。高周波数の係数はDCTに比べ大きくなってしまいます。
どんな形かちょっとイメージがわきません。複素数形式のスペクトル(以降複素スペクトルと省略)を直接プロットしてみましょう。
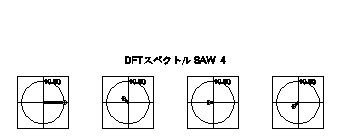
複素スペクトルの形状がつかめたでしょうか?
尚サンプルの数が多くなると一般的には振幅と位相を別々に表示することを行います。
サンプリング数Nを4から32へと大きくして、方形波の入力に対する変換を見てみましょう。
ソースプログラム SciLab_src_DFT4
1/8の期間’1’となるパルス入力です。
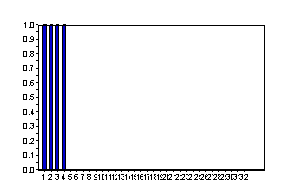
入力パルス(方形波)
変換結果は以下の通り対称性のあるスペクトルになっています。
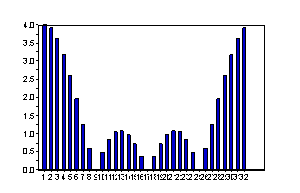
絶対値:|y|
単一周波数のSin波をDFTしてみましょう。黒の線で下の方にプロットされたものが時間領域での入力信号です。32Hzの信号を1秒分、128サンプルしています。
それに対する周波数域への変換結果を、青で重ねて表示してみました(手抜きです)。32Hzにスペクトルが立っているのが確認できます。
ソースプログラム SciLab_src_DFT5
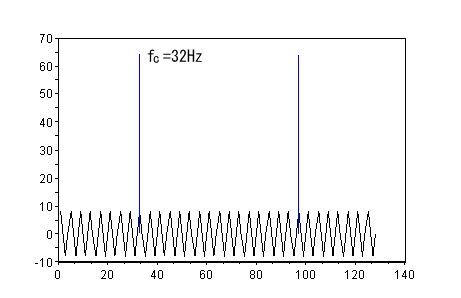
この32Hzの波を搬送波として、8HzのSin波で振幅変調してみましょう。入力信号が8Hzでうねっています。搬送波の32Hzスペクトルの脇に変調波の周波数巾だけ離れて変調スペクトルが立ちました。
ソースプログラム SciLab_src_DFT6
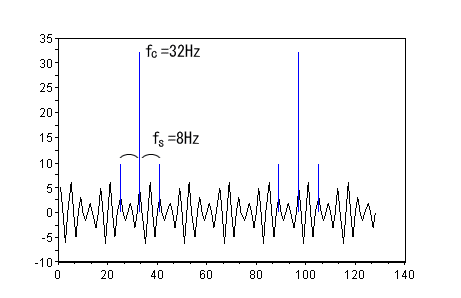
この巾が無線通信なので言うところの送信帯域に当たります。つまり高速なデータを送るためには広い帯域が必要だと言う事が理解できます。
ところで、変換行列の成分の内、共通の部分を以下の様に括り出してみましょう。
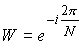
これは回転因子(Twiddle factor)として呼ばれ、aの成分は以下の様にシンプルな形で表現できます。
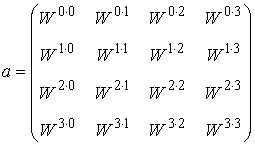
0行0列から数えたK行L列の成分を回転因子を用いて表すと、以下の様にとすっきりとした形で表現できます。
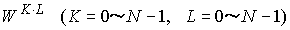
そろそろまとめと併せて、離散フーリエ変換の表記を一般的な教科書に合わせておきましょう。
一般的に入力ベクトルはxのままですが、変換行列aは通常F、さらに変換後の周波数ベクトルyは大文字のXを使うのがスタンダードです。
離散フーリエ変換(DFT): 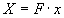
離散フーリエ逆変換(IDFT): 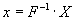
尚、IDFTは変換行列の逆行列と複素共役の関係 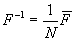 により、 により、
IDFT: 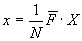
を実際には利用します。この場合の複素共役は、単に行列の成分を構成する回転因子の指数部の符号を、反転させるだけで済むからです。
--------------------------------------------------------
ニュース! 本HP 工業数学が工学社より出版されました。

--------------------------------------------------------
以下本書増強部のダイジェストです。詳細は本書にてご確認ください。
尚、書籍には数式の動作確認をSilabによりステップバイステップで学習可能な工夫をしております。
1.5 フーリエ変換・フーリエ級数との関係
離散フーリエ変換(DFT)の原理を線形方程式(連立方程式や行列)の延長としてを理解してきました。
『どんな複雑な形の波も単純な波の足し合わせで表現できる』の不思議は解消されてのではと思います。
フーリエ級数
下記の式の様に、繰り返し区間Tの三角関数波(複素指数関数)を基底とし、それぞれに係数(複素スペクトル)を掛けて足し合わせると目標の信号を生成できます。ω0は基本角周波数で、Tが1秒なら2πRad/S(1Hz)に相当します。
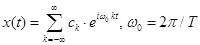
DFTと考え方は同じで逆変換R=B・Sに相当しています。
x(t)を目標信号として各基底の成分(複素スペクトル)を求める式です。
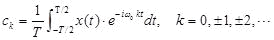
DFTの順変換S=A・Rに相当します。Ckは関数として数式を解いて求めます。
求めたCkはフーリエ係数と呼ばれ、最初に出てきた下記数式に代入すると、x(t)を級数展開したことになります。
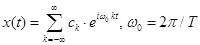
実例で確認するために、数式処理ソフトのMaximaを利用して簡単な実験をしてみましょう。
Maximaはフリーソフトではありますが、Mathematicaのような数式処理が可能で、フーリエ変換の理解には適しているかもしれません。
scilabと同様、興味のある方は是非ダウンロードして試してみてください。(尚以下のMaximaによる実験は[特講]工業数学には未掲載です)
|
Maxima参考プログラム(右クリックでファイルを保存)
実験準備として初期設定。Nはフーリエ係数の数(実際はN+1個)。繰り返し周期Tは1秒、したがって基本周波数:f0は1Hz。
kill(all)$
N:8$ k:makelist(k-N/2,k,0,N);T:1$ f0:1/T$
x:1$ a:1/2;
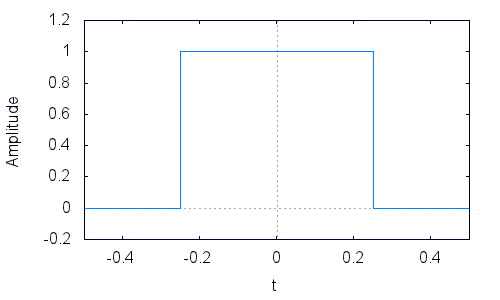
以下図の様なa=0.5S幅のパルスを合成目標(R)とする。
計算の簡便化のため、xはレベル”1”の信号とし、非ゼロ区間のみ(つまりパルス幅:
a=±0.25の範囲)で定積分する。
以下行は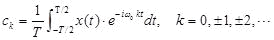 の演算に相当。 の演算に相当。
(説明のしやすさのため、角周波数ωの代わりに周波数fを使っています)
A:exp(-%i*2*%pi*f0*k*t);
C:expand(integrate(A*x,t,-a/2,a/2))/T;
*前述の通り、積分範囲はパルス幅: a=±0.25としています。(手抜きですが問題ありません)
フーリエ係数Cの算出結果
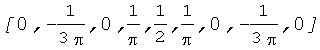
今回は時間信号を偶関数に選んだため、9個の実数係数が得られました。尚、通常、フーリエ係数は複素数です。
形状確認のためCkをプロット
wxplot2d([discrete,k/T,realpart(C)],[style,[points,2,1,1]],[xlabel,"f[Hz]"],[ylabel,"Ck"]);
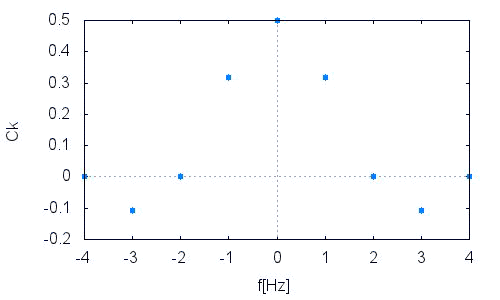
sinc関数の形状をした離散信号Ckです。
次に、この算出したフーリエ係数を使って、入力した時間領域の目標信号xを再現(三角関数の足し合わせによる合成)してみます。
以下は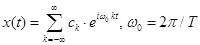 の演算。総和Σ演算の代わりにリスト間で積和演算(ドット積 ”・”)し、xxに代入。 の演算。総和Σ演算の代わりにリスト間で積和演算(ドット積 ”・”)し、xxに代入。
B:exp(%i*2*%pi*f0*k*t);
xx:B.C;
演算結果:
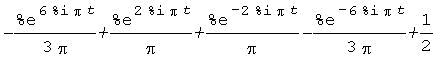
1Hzと3Hzのcos波+DC波(0Hzのcos波)からなる複素指数関数となりました。*
*各複素指数関数の項で、同一周波数の項は正負のペアとなっており、cos関数の複素指数関数表現(オイラーの公式)となっています。
目標信号R(赤)と重ねてプロットしてみましょう。
plot2d([realpart(xx),R(t)],[t,-T/2,T/2],[ylabel,"Amplitude"]);
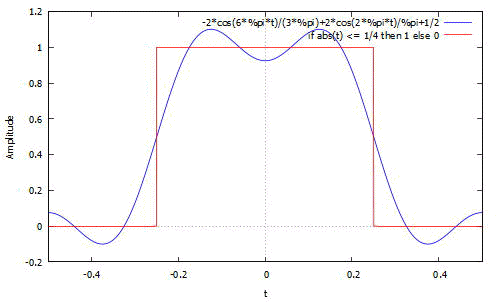
まあ、何となく目標信号のパルスに似てなくはは無いですね・・・
尚、時間信号はあくまで複素指数関数による表現であり、”連続”となっていることに留意してください。
プロット範囲を広げてみましょう。xxは関数なので再計算は不要です。
wxplot2d(realpart(xx),[t,-4*T/2,4*T/2],[ylabel,"Amplitude"]);
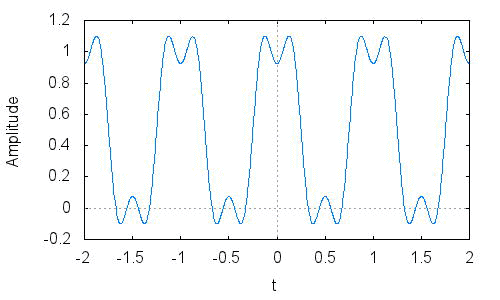
成程。フーリエ級数の定義通り、周期Tの周期波となっています。
パルスの角が丸まっているので、高周波数側の成分が不足しているようです。目標関数が再現されているかの確認には、もう少し精度がほしいところですです。
高周波数側に広げるために、基本周波数は変えずに、N:32と係数の数を増やしてして再計算してみましょう。
Ckのプロットです。
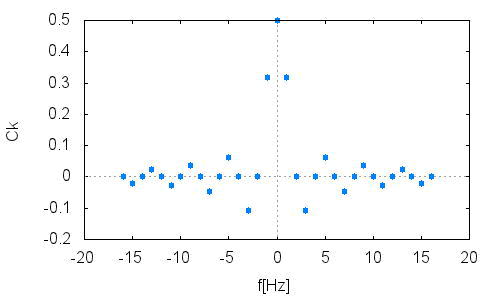
sinc関数のすそ野が広がってきました。ある程度、高周波数側の係数が確保できたようです。
このCkにより時間信号を、再度合成してみましょう。
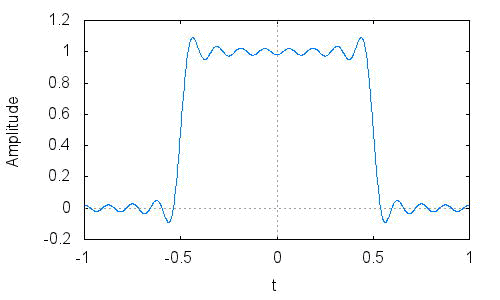
角張って、目標信号の方形波にかなり近づきました。
k=±∞により正確に目標信号を再現できることが理解できます。
|
フーリエ変換の原点となる三角関数形フーリエ級数の定義を下記表に複素形と対比させて記述しました。
前述のMaximaの実験で確認した通り、周波数が離散値となっています。フーリエ変換ファミリーとして分類すると“連続時間・離散周波数フーリエ変換”でしょうか。
フーリエ変換(Fourier Transform,
FT)・フーリエ積分(Fourier integral)
前述の通り、フーリエ級数は周期Tの波を前提に行う演算です。
以下の様に繰り返しが無い孤立波を扱うことはできません。
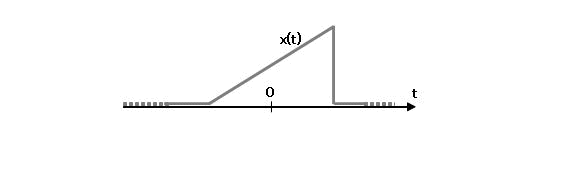
そこで級数からフーリエ積分への拡張が必要となります。
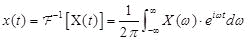
上記の積分式は周波数関数X(ω)と基底関数eiωtより目標関数、つまり時間関数x(t)が生成されることを示しています。
この様に周波数関数X(ω)から時間関数x(t)を求める操作をフーリエ逆変換と呼びます。
時間関数から周波数関数を求める式は
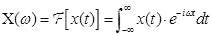
となります。これは時間関数x(t)から周波数関数X(ω)への変換であり、フーリエ変換とよびます。
これは以下の様にフーリエ級数の繰り返し周期Tを無限大に引き伸ばした極限として求められます。
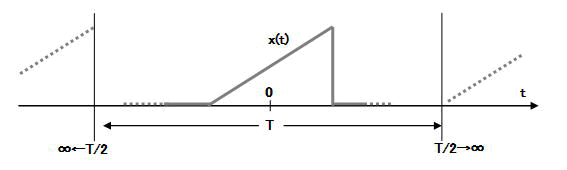
「孤立波」というからには観測範囲(つまりT)を無限大とする必要があります。こっそりどこかで繰り返してないか?確認するためにも承知せざるを得ません。
フーリエ変換は時間も周波数も連続時間なので“連続時間・連続周波数フーリエ変換”とよんで良いかもしれません。
離散フーリエ変換(DFT)が数値解析ベースでデジタル信号処理で利用されているのに対し、フーリエ変換(FT)は数式解析ベースで物理の論理的解析に応用されているといった関係でしょうか。
尚、DFTの理論的な基盤はフーリエ変換になります。DFTは連続時間信号(アナログ信号)として定義されているδ関数列(櫛型関数)を、同じくアナログの目標信号で変調(サンプリング処理)したケースとして定式化されます。つまりDFTはFTの一応用分野と言えます。
1.6 δ関数による離散化(アナログからデジタルへ)
フーリエ変換は連続時間の周波数解析などに使われます。いわばアナログのツールですね。古い歴史に裏打ちされた数学的背景をもっています。
一方DFTはデジタル時代の信号処理ツールです。背後に連続時間システムから離散時間システムへの移行が存在します。その中で重要な役割を担っているのがδ関数といえます。
δ関数(アナログ版)
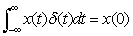 を満たす関数 を満たす関数
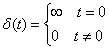
かつ、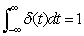
この連続時間信号として定義された信号は「ディラックのδ」とも呼ばれています。
無限大の振幅を持つが、積分すると1となります。フーリエ変換のように連続時間で扱う場合に使用します。
(このδ関数は通常の関数ではなく、超関数として定義されています。実はsin波などの三角関数ををフーリエ変換したスペクトルとして現れ、このδが定式化されたことによって、はじめてフーリエ変換は数学的に確立された論理的背景を持つようになったと言われているようです。そういえばディラックも彼の量子論にδを持ち込んだ時に、その論理的背景に疑問を持たれたようです)
δ関数(デジタル版)
DFTの様に離散信号を扱う場合に使用します。
以下の図の様に、時刻0で1の大きさの信号です。「単位インパルス信号」、「ユニットインパルス」などと、呼ぶ場合もあります。
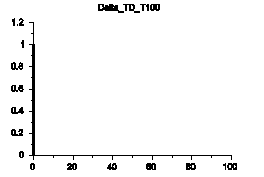
アナログ版のδ関数を理解することを目的に少々このデジタル版δをいじってみましょう。どんな性質があるのか、Scilabで簡単に実験することができます。
まずは、このδ関数をDFTしてみます。
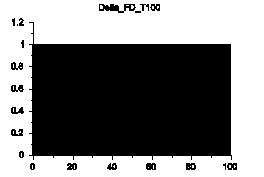
スペクトルはすべて1となりました。真っ黒に塗りつぶされています。
δ信号列(櫛型関数)
δ信号を連続生成させてみます。
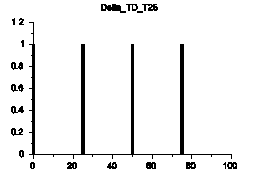
これのスペクトルはどうなっているでしょうか?
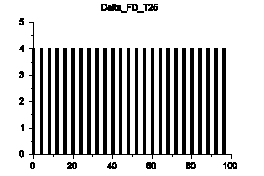
なんと周波数領域でもδ関数列(櫛型関数)になりました!
なんだか直感に反する結果です。δ信号のスペクトルから想像しがたいものがあります。背後にどんなメカニズムが働いているのでしょうか?
8x8変換行列に入力信号xとして周期4のδ関数列[1 0 0 0 1 0 0 0]を掛けてみます。
スペクトルとして出力される信号yは、以下のように1列目と5列目が抜き出され加算された結果となります。
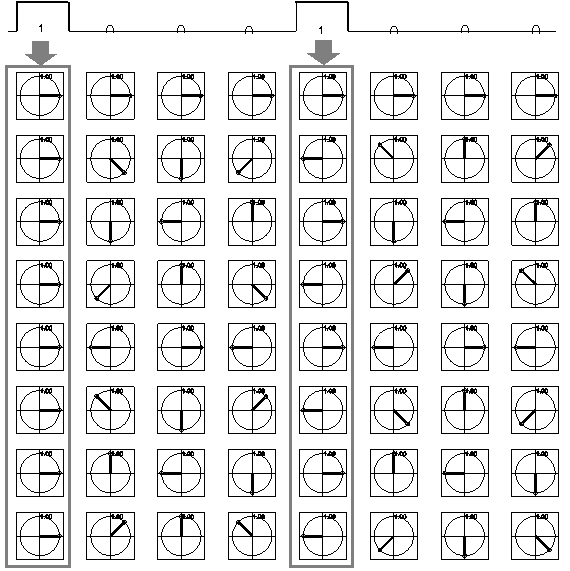
これを良く見ると、奇数行では同位相で強調され2倍の信号出力となり、偶数行では互いに打ち消しあって0となっています。なるほど周期2のδ関数列[1
0 1 0 1 0 1 0]がスペクトルとして出力されています。
次に周期2のδ関数列[1 0 1 0 1 0 1 0]を入力した場合は、3列目+7列目が、またしても巧妙に先ほどの1列+5列の結果と強調・打消しが行われ周期4のδ関数列が生成される事が理解できます。
つまり入力する時間信号の周期が小さくなると、打ち消される行が多くなり周波数側のδ関数の周期が大きくなるという、巧妙なメカニズムが働いています。
この様な特殊な振る舞いをするδ関数列を、サンプル目標の信号に掛けます。その結果δ関数の定義より目標信号の値を積分値として持つδ関数列ができます。
実際にサンプル目標信号を「4Hzのsin波+DCオフセット」をとして実験してみます。
この操作は以前の振幅変調の実験と同様、櫛型関数をキャリアとして目標信号で変調しているとも取れます。
以下の図が掛け合わせた結果です。
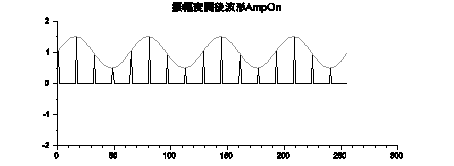
全区間を1Sとすると、パルス間隔:T=1/16Sのδ列(16Hzのキャリア)が4Hzでうねっています。前回の実験とちょっと似た雰囲気です。
以下がDFTにより求めたスペクトルです。
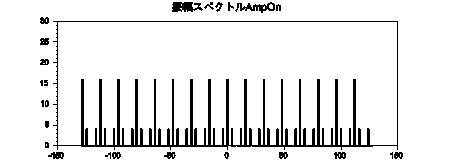
前回のsin波をキャリアとした変調と同様、目標信号の周波数:4Hz分、左右に側帯波を伴ったスペクトルとなりました。なお、中心周波数は変調時のオフセットとして加えたDC成分です。
しかし今回はそれらのコピーが繰り返し発生しています。繰り返し周期は16Hz(=1/T)です。これがδ関数列をキャリアとして変行した場合の特徴です。
離散時間フーリエ変換(DTFT)
前述の結果は、通常の振幅変調でキャリアとして使うsin波の代わりに、δ関数列と掛け合わせることにより、目標信号のDC成分や4Hzに対応する周波数成分を採取することができたと言う事です。

何がうれしいのか?・・・ フーリエ変換前の信号xsはδパルス以外はすべてゼロ(情報なし)という、非常にダイエット化された信号になっています。
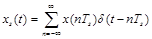
それでも、それをフーリエ変換すると、さもそれらしいとスペクトルは得られるみたいだ?・・・ と言う事です。
これを数式で表すと
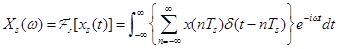
{・}内左の項が目標信号で右がδ関数列です。これをフーリエ積分しています。
さらに変形すると、
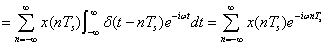
を得ます。
この式は実験結果が示す通り2π/Ts[rad/S] (=1/Ts[Hz]) の繰り返し周期です。
これをサンプル前の連続時間信号のフーリエ変換X(ω)と比較してみましょう。
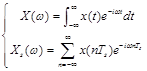
サンプル間隔Tsを十分小さくとるとX(ω)を近似出来そうです。ただし、周波数領域の周期2π/Ts繰り返しが示す通り、明らかに周波数高い部分は近似できそうにありません。
また実験で確認した通り、δ列変調によりスペクトルの大きさは1/Ts倍となっています。これはフーリエ変換の積分式と比較すると離散時間フーリエ変換(総和演算)の式では”dt”に対応する部分が抜けているための様です。
以下逆変換の式です。
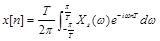
*[特講]工業数学では本式の先頭に掛かるTが抜けていました。正誤表を更新します。
離散時間フーリエ変換(DTFT)の周波数領域は連続信号です。周波数領域での数理的関数解析が可能ですが、デジタル信号処理は難しそうです。またこの様に逆変換時には積分処理が必要となります。
フルデジタル処理のためには周波数領域も離散化したくなります。そして離散フーリエ変換(DFT)がその答えとなります。
数式処理ソフトのMaximaを利用して簡単な実験をしてみましょう。
(尚以下のMaximaによる実験は[特講]工業数学には未掲載です)
|
Maxima参考プログラム(右クリックでファイルを保存)
実験準備として初期設定。時間信号サンプル数:N=8。 尚、このNは波形記述用の作業ウインドサイズであり、有効な時間信号部(非ゼロ信号)全体をカバーしていれば良く、信号処理上特に重要なものではありません。
kill(all)$ N:8$ Ts:1/N$
n:makelist(n,n,0,N-1); t:Ts*n;
時間インデックスnの内容エコー表示
[0,1,2,3,4,5,6,7]
サンプリングタイミングtの内容エコー表示
[0, 1/8, 1/4, 3/8, 1/2, 5/8, 3/4, 7/8]
簡単な例としてサンプル列x[n] (=x(nT)の値)を
x:[1,1,1,0,0,0,0,0];
とします。
この場合先頭(左端の”1”)が時刻0です。 プロットすると、
wxplot2d([discrete,n,x],[y,-0.2,1.2],[style,[points,2,1,1]]);
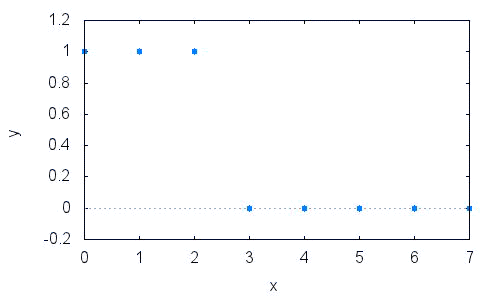
全体を1Sとすると、3/8[S]のパルスがサンプル目標信号となります。
まずは、以下のコマンドで離散時間フーリエ変換(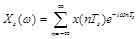 )を実施してみましょう。 )を実施してみましょう。
Xs:sum(exp(-%i*w*Ts*n)*x[n+1],n,0,N-1);
出力されたXsは
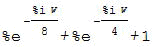
となりました。3項から成る複素指数関数の和となっています。Maximaなので数値出力ではないことに注目してください。
この様に離散時間フーリエ変換の場合、周波数領域では関数で表された連続周波数信号となります。
これをプロットしてみましょう。フーリエスペクトルは基本的に複素数であるため、絶対値をとります。
plot2d(abs(Xs),[w,-4*%pi/Ts,4*%pi/Ts]);
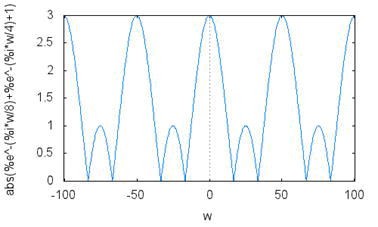
周波数の繰り返しが分かるように、多目にx軸をプロットしました。
Tsは1/8Sなので2π/Ts=16π≒50.3[rad/S]が繰り返し単位です。
逆変換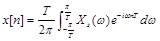 によりサンプル列を再現してみましょう。 によりサンプル列を再現してみましょう。
Maximaのコマンドは
xo:expand(Ts*integrate(exp(%i*w*Ts*n)*Xs,w,-%pi/Ts,%pi/Ts)/(2*%pi));
です。Xsは数式でありintegrateコマンドで数式を直接変形(定積分)します。
その出力結果は、
[1,1,1,0,0,0,0,0]
上手く再現されています。
|
以上、離散時間フーリエ変換・逆変換とはどのような物かの簡単な説明です。
ところで、フーリエ変換への近似はどの程度成り立っているのでしょうか?。離散時間システムの特徴を理解することも含めて、もう少しMaximaで実験を続けてみましょう。
方形波(パルス)のフーリエ変換Xは、sinc関数と呼ばれ、以下の式で表されます。尚、この関数は各所に現れる非常に重要な関数です。
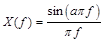 あるいは あるいは 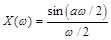
時刻0を中心とした長さ3/8[S]パルスの場合のフーリエ変換:X(ω)をプロットします。 aはパルスの長さ、wは角周波数です。
wxplot2d([sin(a*w/2)/(w/2)],[w,-10*%pi/Ts,10*%pi/Ts],[y,-0.2,0.5]);
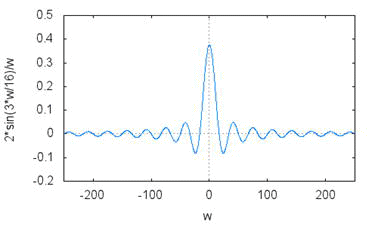
これを正答信号とし、離散時間フーリエ変換と比較します。
この図の様に、sinc関数の裾野は左右に小さくなりながらも周波数軸上無限に広がっているので、もし途中で「ちょん切った」場合は、正しい信号ではなくなります。
まずは現状のXsの形状を確認します。スペクトルは複素数信号のためabs()により振幅のみ表示しているので、形状が分かりにくいですね。
周波数信号が実数になるように、実験条件を少し変えましょう。そのために時間軸の信号を少しずらして偶関数にします。4番目が時刻0をとなるように処理を変更します。
x:[0,0,1,1,1,0,0,0];
以下の通り時刻0を中心とし、幅3の遇関数になります。
wxplot2d([discrete,n-3,x]);
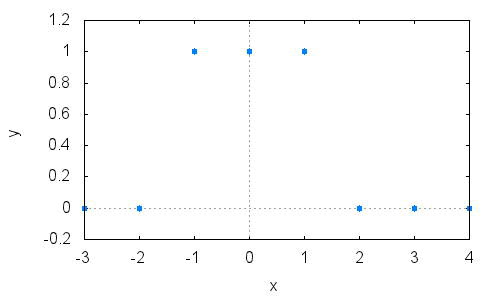
同様にDTFTしてXsを求めます。
Xs:sum(exp(-%i*w*Ts*(n-3))*x[n+1],n,0,N-1);
Xsの結果出力です。
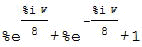
この数式はの最初の二つの項はペアとなっており、cos関数の複素指数関数表現(オイラーの公式)です。実数化できました。
プロットすると、
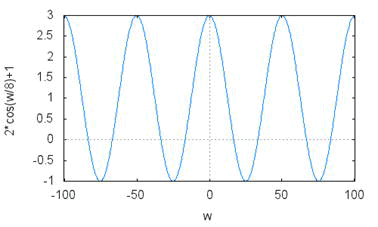
明らかに期待していたsinc関数とは異なります。sinc関数を重ねてプロット(赤)しと比較してみましょう。DTFTによるXsは振幅が1/Ts倍になっているためTsを掛けて補正し表示しています。
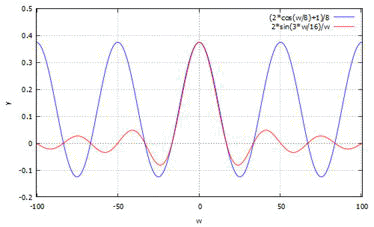
しかしこの関数も、周波数の低い範囲(・・・なんとなくcos波の最初の一山分、±20[rad/S]程度)ではsinc関数と形状が似ているよです。
サンプリング数を増やしてみます。信号xの形状(1・0比)は以下の様に変えないようにします。
x:[0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0];
wxplot2d([discrete,n-11,x],[y,-0.2,1.2],[style,[points,2,1,1]]);
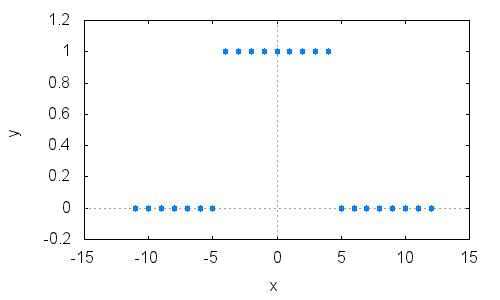
Xs:sum(exp(-%i*w*Ts*n)*x[n+12],n,-11,12);
Xsの結果出力です。
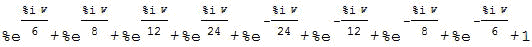
おお、動員される三角関数(cos)が増えてきました。(もっとも、これは計算式を良く見ると、単純にxの中の信号"1"の数に対応しているだけだということが、理解できますが・・・)
この関数のプロット結果です。
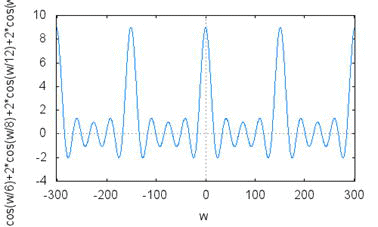
繰り返し周期の間隔が広がり、sinc関数の裾野が見えてきました。
sincと重ねて比較プロット。
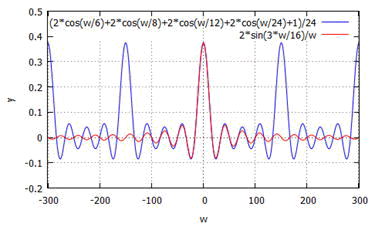
中央の山に加えて左右隣の1山も近似して来たでしょうか?ある程度高い周波数まで近似が広がって来た様に見えます。
・・・と、この様な調子でサンプリング数をどんどん増やしいくと、だんだん本物のsinc関数に相似してきて、完璧では無いにしろ実用上問題な精度が得られそうです。
後程説明しますが、サンプリング定理により、1/(2Ts)[Hz]未満の信号まで正確にサンプリング(標本化)できます。
またサンプリングされた信号より元の連続時間信号を復元できます。ただし元の信号には1/(2Ts)[Hz]以上の信号が含まれていない場合です。これを帯域制限された信号と言います。
|
尚、x[n] := x(nTs)として説明していますが、示した様にサンプリング間隔Tsによりスペクトルの大きさが変ってきます。
そこで予めδ列による変調時にTsを乗じておくと、スペクトルの大きさがTs不変となり、かつフーリエ変換とスペクトルの大きさがそろいます。そうすると、標本化されたデータ列との関係は
x[n] := Ts・x(nTs)
となり、離散時間フーリエ変換式の頭にもTsが付くことになります。
以上、連続時間信号の例として方形波をフーリエ変換、離散時間フーリエ変換しそれぞれの周波数領域での信号形状を比較する実験でした。
Maxima参考プログラム(右クリックでファイルを保存)
尚、DTFTの計算方法として、サンプリング間隔は時間領域信号xのリストの要素数Nを使い、Ts=1/Nで算出しました。しかし時間スケールさえ頭に入っていれば、Tsは直接指定しても問題ありません。
そもそも、実験例からお分かりの通り、xの信号値”0”以外の値が有る部分のみXsに実体化(複素指数関数の項として存在)されます。Nを大きくして、ゼロ詰めをするのと、NをそのままにしてTsを小さくすることは同じことです。
整理すると
1)離散時間フーリエ変換では高周波数側に折り返しがあり、高周波数側では誤差が生じる
2)サンプリング周期Tsを小さくしていく(サンプリング数を増やす)と周波数軸上の繰り返し間隔が広がり、スペクトル形状がsinc関数に近づいてくる。つまり近似が良くなる。
3)DTFTは簡単だが、逆変換のIDTFTは(少々手間のかかる)積分演算が必要。時間領域に戻すのが大変なので、周波数領域デジタル信号処理には不向き。
そこで周波数領域も離散化したくなります。
つまり、時間信号をこのように

離散化して入力すると、
こんな感じで

周波数領域の信号も離散化していてほしいですね。
そうです。Maximaによるフーリエ級数の実験見覚えがあると思いますが、これはフーリエ係数
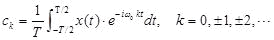
のプロットです。
実験では以下の様にω0の代わりにf0を使いましたが、係数の差が有るだけで基本的に同じことです。
exp(-%i*2*%pi*f0*k*t)
ポイントは変換式の周波数変数を連続ωから離散ω0に変えることです。言い換えると、離散周波数化のためにはフーリエ級数と同様、『時間信号は繰り返しTの周期波を前提とする』 必要が有るとになります。
サンプリング周期Tsを1秒とおき、連続時間との関係を一旦忘れましょう。
また、原理的に繰り返し区間内のサンプリング点数と離散化周波数の点数は同じになります。したがって、周波数、時間共通の母数Nにより
離散フーリエ変換 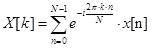
離散フーリエ逆変換 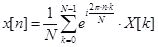
こうするとデータ列間換の変換に集中できます。この場合周波数はサンプリング周波数を1とした正規化周波数(たとえばN=8の場合の基本周波数は1/8に相当)となります。
連続時間との関係を考慮する必要がある場合、たとえばフーリエ変換と比較する場合周波数信号の振幅は1/Tsになっているので注意が必要です。
kを[-3〜+4]の様に負の周波数と1対1対応させるのが素直ですが、デジタル処理上負の指標はうっとうしいので、以下の様に等価となる正の範囲で対応させて演算します。
指標k
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 1周期1秒の場合の周波数[Hz] |
±0 |
+1 |
+2 |
+3 |
±4 |
-3 |
-2 |
-1 |
これはサンプリング周波数の1/2で周波数が折り返す原理を利用したものです。
以上[特講]工業数学で追加された「DFTとFTの関係」の概要と「δ関数による離散化のメカニズム」の概説(かなり駆け足ですが・・・)です。
概説に飽き足らない方、詳細ご興味のある方はぜひ下記、[特講]工業数学のご購読ください。scilabを使った実験で上記の内容の詳細を確認できます。その他見どころ、沢山あります!
--------------------------------------------------------
ニュース! 本HP 工業数学が工学社より出版されました。

--------------------------------------------------------
尚、Maximaによる実験は、本書での解説の前ふり、補足的な位置付けです。本書と併せて通読されると、より理解が深まるものと思います。
|

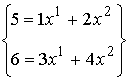
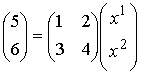 →
→ 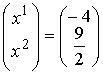
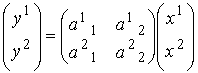

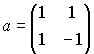
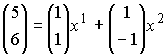
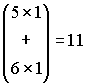 ,
, 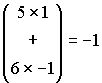

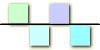
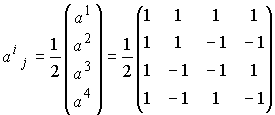
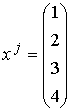 →
→