信号処理の基礎

　　　　　　　　　ニュース！　本ＨＰ工業数学が工学社より出版されます。

Appendix　.１　行列の分類メモ

正則行列(Regular matrix)：

　逆行列(Inverse matrix)が存在する正方行列。可逆行列(Invertible matrix)とも言う。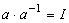

　　　　　　　

正規行列：

　以下を満たす正方行列。随伴行列（Adjoin matrix)との積の順序が可換である。

　　　　　　

＊ユニタリー行列、エルミート行列は正規行列である。
＊固有値は実数となる。重根があっても対角化可能。

直交行列（Orthognal matrix)：

　転置行列と、逆行列が等しい実正方行列。

　　　　　　

　　　例
　　　　　　　は直交行列です。
　　　　　　逆行列：　　　転置行列：　

ユニタリー行列（Unitary matrix)：

　転置し、複素共役を取った随伴行列（Adjoin matrix)と、逆行列が等しい。

　　　　　　

　　　例
　　　　　　　はユニタリー行列です。
　　　　　　逆行列：　　　随伴行列：　

対称行列（Symmetric matrix)：

　転置しても、元の行列と等しい。

　　　　　

　　　　例
　　　　　は対称行列です。
　　　　　　転置行列：

エルミート行列(Hermitian matrix)：

　転置し、複素共役を取った随伴行列と、元の行列が等しい。

　　　　　

　　　　例
　　　　　　はエルミート行列です。
　　　　　　随伴行列：

＊実数の対称行列を包含しており、対称行列を複素数に拡張したものと言える。